探索离散傅立叶变换：入门与理解

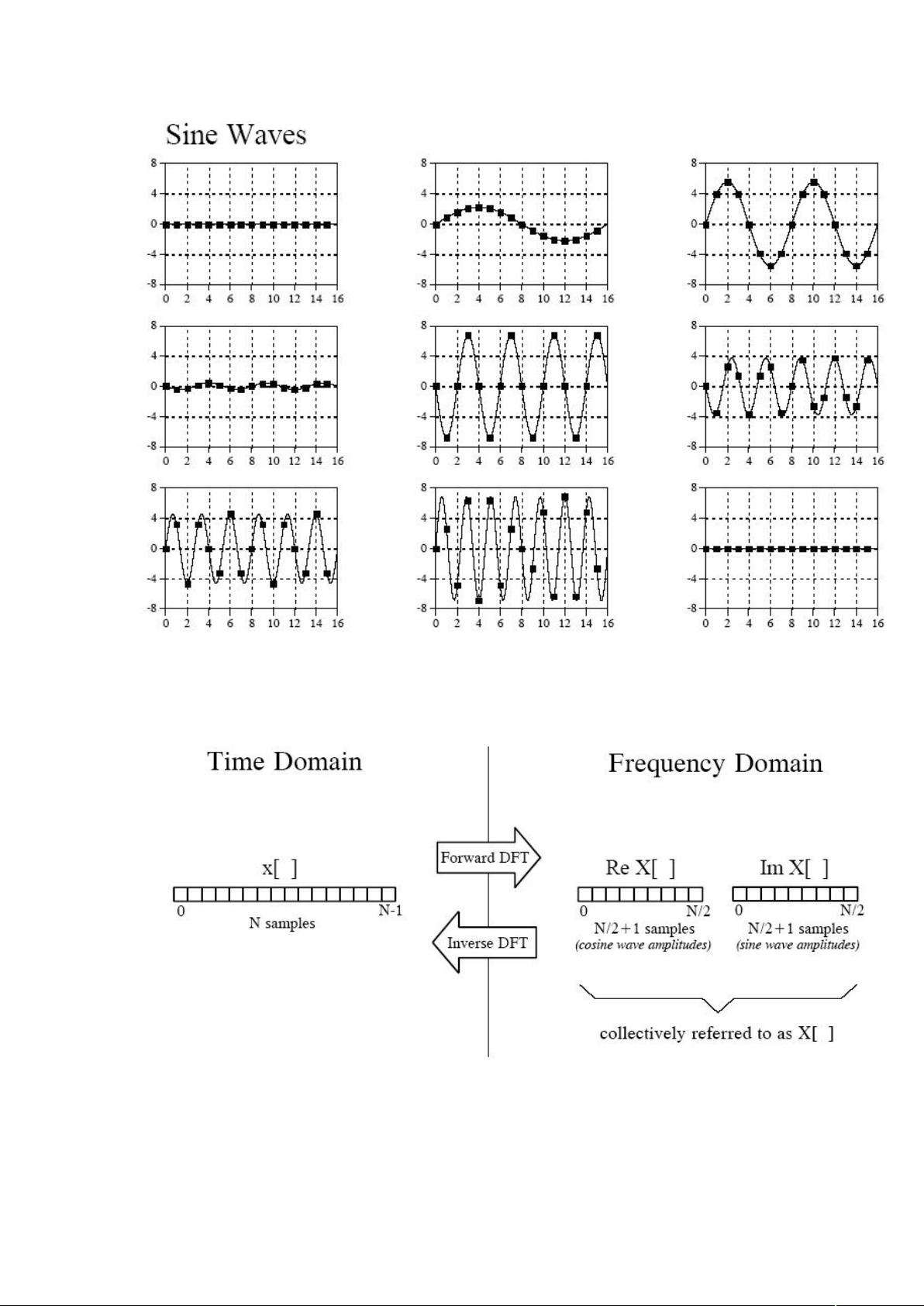
傅立叶变换是信号分析领域中的核心概念，它最初由法国数学家和物理学家Jean Baptiste Joseph Fourier在1807年提出，主要探讨如何用正弦曲线组合来描述连续周期信号。傅立叶变换的重要性在于其能将复杂的时域信号分解为一组简单的频率分量，这对于理解信号的频谱特性至关重要。 理解离散傅立叶变换（DFT）对于信号处理和通信工程尤为重要，特别是对于初学者来说，传统的教科书常常过于理论化，导致许多概念难以直观把握。Steven W. Smith的电子书提供了一个很好的入门资源，该书以浅显易懂的方式逐步介绍了DFT的原理。Smith教授从傅立叶级数变换出发，阐述了傅立叶变换的基本公式，强调了耐心和一定的高等数学基础知识在理解这一概念中的必要性。 傅立叶变换的核心思想是任何连续周期信号都可以表示为一系列正弦波的线性组合，这些正弦波的频率对应了信号的不同成分。然而，早期对于这一理论的接受并不普遍，特别受到拉格朗日的质疑，他认为某些非平滑信号（如方波）无法用这种方法准确表示。尽管如此，傅立叶变换的理论最终被证明是强大的工具，广泛应用于信号处理、图像处理、音频分析等领域，如在数字信号处理中，DFT被用于滤波、频谱分析和通信系统的频谱效率优化。 要深入学习傅立叶变换，建议阅读Smith的电子书，通过实践和实例来掌握变换的计算方法和应用场景。同时，理解级数变换和复数运算的概念也是必不可少的。值得注意的是，尽管傅立叶变换最初是针对连续信号设计的，但在离散信号处理中，离散傅立叶变换（DFT）通过采样和窗口函数等技术，将连续信号转化为离散形式，使其成为现代电子设备中不可或缺的技术。 理解傅立叶变换不仅是对信号分析理论的掌握，也是一种对信号世界内在结构的洞察，对于从事电子工程、通信工程以及信号处理的人来说，是一项至关重要的技能。通过实践和不断的学习，你将能更好地应用这一工具，解决实际问题。