混沌控制研究：机械式离心系统反馈建模与分析

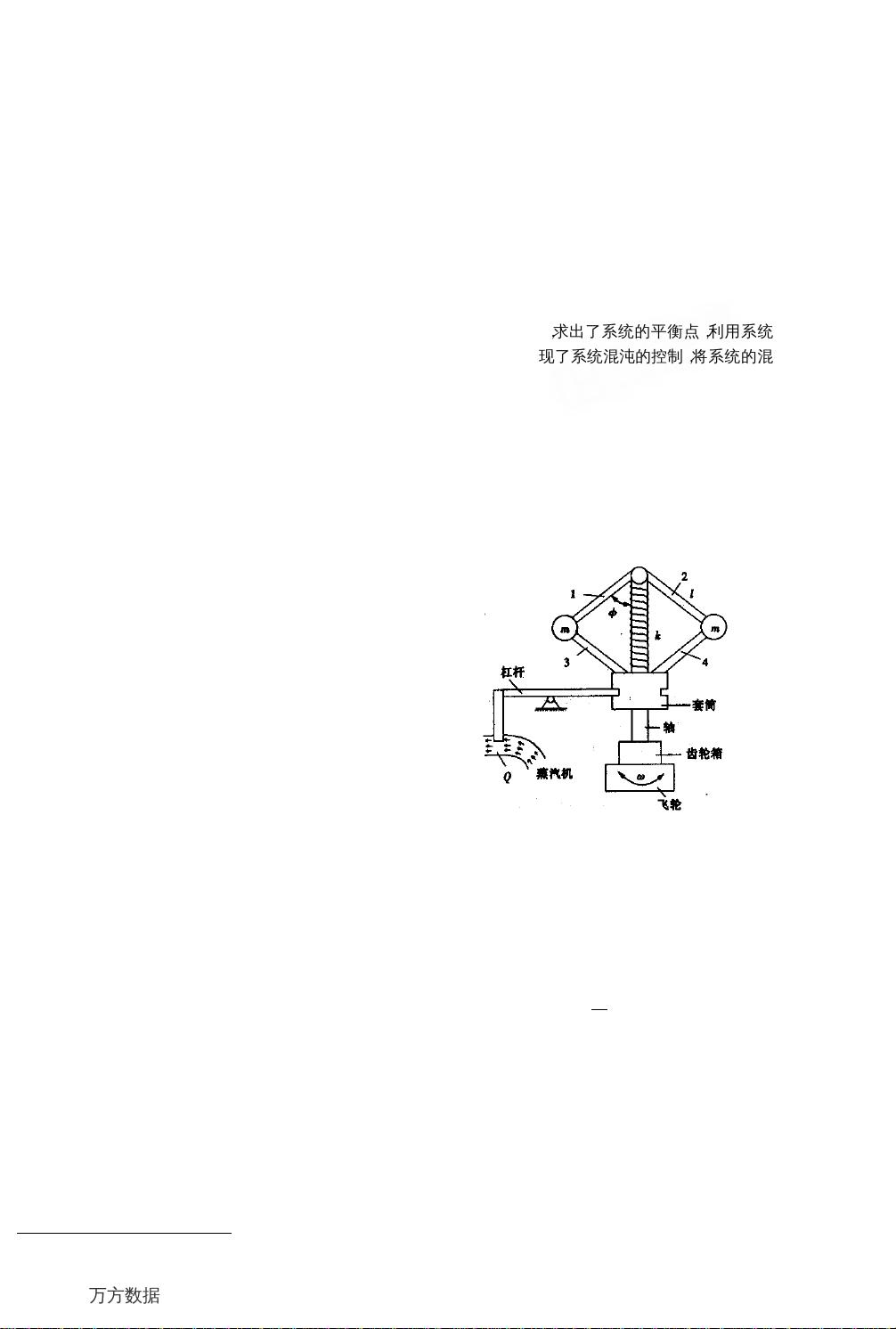
"本文探讨了机械式离心调速器系统的混沌反馈建模分析，通过拉格朗日方程建立动力学模型，研究混沌现象的形成，并利用连续变量反馈控制实现混沌控制，将系统从混沌状态引导至稳定的周期轨道。" 在机械式离心调速器系统中，混沌反馈建模分析是理解其复杂动态行为的关键。系统通常由发动机驱动的飞轮、齿轮箱、旋转轴、铰接杆、质量球、套筒和弹簧等部件组成。通过拉格朗日方程，我们可以建立描述系统运动的数学模型，这有助于我们理解系统在不同条件下的动力学特性。 首先，基于拉格朗日方程，我们可以推导出系统的动力学方程，这些方程描述了各部件之间的相互作用以及系统能量的变化。通过解这些方程，我们可以找到系统的平衡点，即系统不受外力影响时静止或稳定运动的状态。然后，通过分析系统的相图，可以揭示系统在不同参数下的动态行为，例如周期运动、准周期运动或混沌运动。 混沌是一种复杂的非线性动态行为，表现为对初始条件的高度敏感性，使得长期预测变得几乎不可能。在机械式离心调速器系统中，混沌可能源于系统参数的微小变化，如弹簧倔强系数、质量分布或杆的长度等。通过相图和映射图，我们可以观察到混沌的形成过程，例如通过分岔图可以看到系统如何从简单周期运动逐步演化为混沌状态。 混沌控制是混沌理论的一个重要应用领域，旨在通过外部干预来操纵混沌系统的行为。文章中提到了连续变量反馈控制方法，这是一种有效的控制策略，可以通过调整反馈参数来改变系统的动力学特性，从而将混沌状态转化为稳定的周期运动。这种方法的应用可以确保系统在实际操作中的可预测性和稳定性，例如在蒸汽机或内燃机的调速过程中。 控制混沌的方法有很多种，包括滑模控制、反馈线性化、Lyapunov函数设计等。在机械式离心调速器系统中，通过适当的控制强度调整，可以将混沌运动控制到一个稳定的周期一轨道，这意味着系统会按照固定的周期重复其运动，这对于保持调速器的稳定运行至关重要。 混沌反馈建模分析对于理解和控制机械式离心调速器这类复杂系统的行为至关重要。通过深入研究混沌现象及其控制策略，我们可以更好地设计和优化此类系统，确保它们在实际应用中的性能和可靠性。