超对称SYK模型中的混沌与随机矩阵分析

57 浏览量更新于2024-07-16 收藏 823KB PDF 举报

"超对称SYK中的混沌和随机矩阵" 这篇学术文章深入探讨了超对称量子力学系统中的混沌现象，特别关注了超对称 SYK（Sachdev-Ye-Kitaev）模型中的混沌行为。SYK模型是一种特殊的量子多体系统，它在低维度量子引力和复杂性理论中有重要应用。文章利用随机矩阵理论，这是一种强大的工具，常用于理解和预测复杂系统的行为，尤其是统计力学和量子混沌领域。作者 Nicholas Hunter-Jones 和 Junyu Liu 来自加州理工学院的量子信息和物质研究所以及沃尔特·伯克理论物理研究所，他们分析了 Wishart-Laguerre 单位元综合作为研究框架，这是随机矩阵理论中的一种特定类型。Wishart-Laguerre 综合通常被用来描述随机协方差矩阵的性质，这在这里是为了探究超对称 SYK 模型的混沌特性。在文章中，研究人员计算了频谱形状因子和框架势，这两个量可以定量地描述混沌和随机性的程度。他们发现与高斯合奏（即最简单的随机矩阵模型）相比，超对称SYK模型的形状因子没有显示出典型的“倾角”机制，这是一个在混沌系统中常见的特征。此外，系统向 Haar 随机动力学的演化也比预期更慢，Haar 测度是单位圆上所有旋转的均匀分布，常被用来表示完全无规的动力学行为。通过随机矩阵分析，作者观察到了与超对称SYK模型预测的一致性，这进一步验证了该模型的理论预言。他们的工作还涉及讨论这些发现对于理解超对称混沌系统的意义，这些系统可能在量子信息处理、量子计算和量子热力学等领域具有潜在的应用。文章的发布日期为2018年，表明了这是该领域相对较新的研究成果，对于进一步理解超对称系统和量子混沌的相互作用提供了重要的理论基础。通过这样的研究，科学家们希望能更好地理解复杂量子系统的行为，从而推动量子物理学和相关技术的发展。

JHEP05(2018)202

diﬀerent. Roughly, we can think of the supersymmetric SYK behaving like the square of

Gaussian random matrices, which are the Wishart ensembles. For more details, see [18] as

well as an extension of the classiﬁcation to the N = 2 supersymmetric models [15].

Speaking generally, there a number of reasons one might wish to consider supersymmet-

ric generalizations of SYK. For instance, much is understood about the low-energy physics

in nearly AdS

spacetimes purportedly dual to the low-energy dynamics in SYK, but the

exact holographic dual of the theory is not know. As many of the best understood exam-

ples of AdS/CFT are supersymmetric, one might hope that this particular construction

might provide guidance on the correct UV completion of the SYK model. Less ambitiously,

considering the supersymmetric models might be useful in contructing higher dimension

analogs [12].

2.2 Spectral form factor

Quantum chaotic systems are often deﬁned to have the spectral statistics of a random ma-

trix. An object familiar in random matrix theory which exhibits these universal properties

is the spectral form factor. We will introduce this object more precisely in our review of

random matrix theory in section 3.1, but the 2-point spectral form factor R

(t, β) can be

given simply in terms of the analytically continued partition function

(t, β) ≡



Z(β, t)Z

∗

(β, t)



, where Z(β, t) ≡ Tr



−βH−itH



, (2.4)

and where the average h·i is taken over an ensemble of Hamiltonians (e.g. SYK, or some

disordered spin system, or a random matrix ensemble). This object was discussed more

recently in [27], where they studied the form factor in SYK and found that the theory

revealed random matrix behavior at late times. From the bulk point of view, one motivation

for studying this object was a simple version of black hole information loss [32]: 2-point

functions appear to decay exponentially in terms of local bulk variables, whereas a discrete

spectrum implies a ﬁnite late-time value. The same inconsistency is apparent in the spectral

form factor.

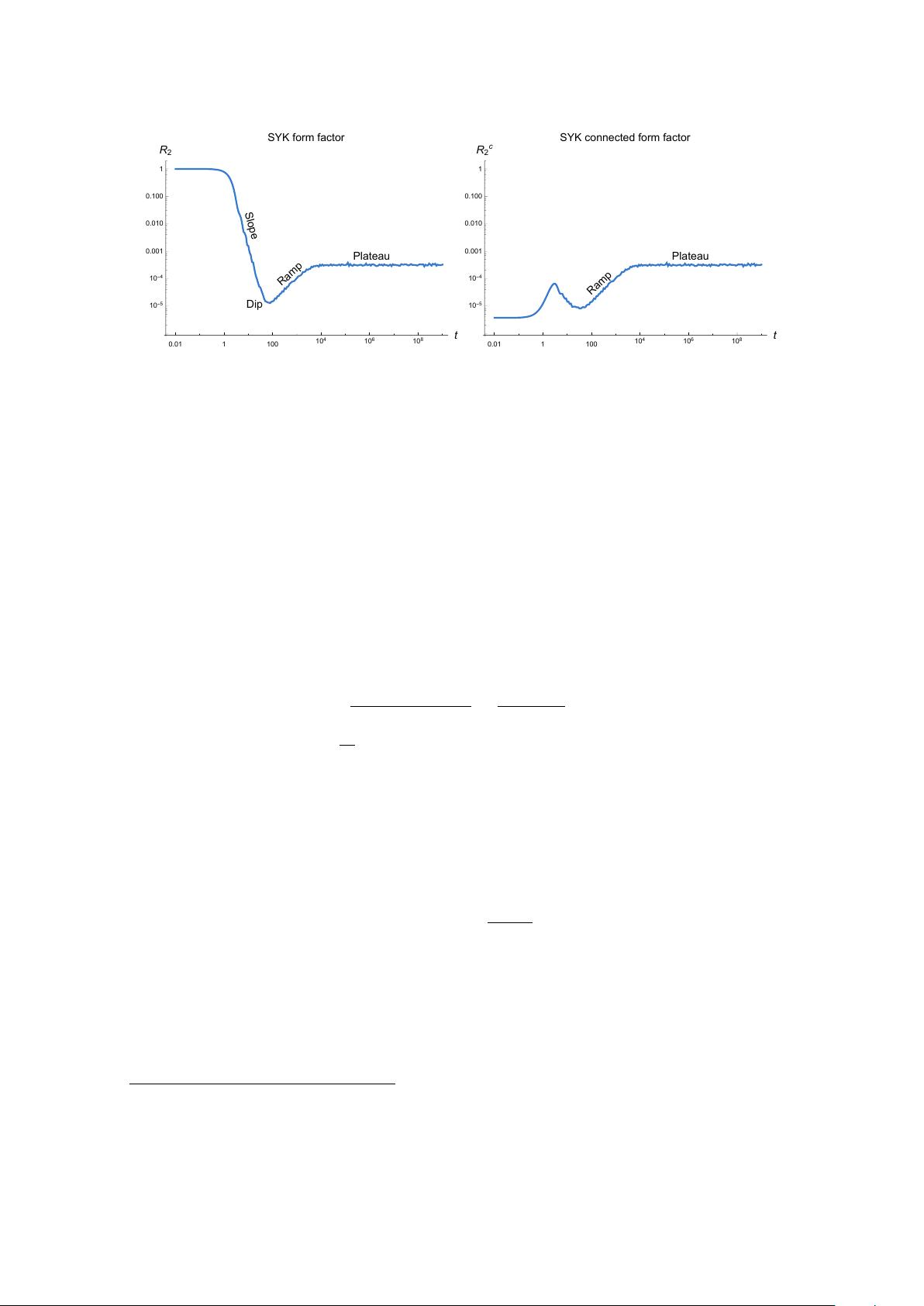
Some characteristic features of the time-evolved form factor R

(t), exhibited in both

the SYK model and in random matrix theories, are: an early time decay from an initial

value called the slope, a crossover at intermediate times called the dip, a steady linear

rise called the ramp, and a late-time ﬂoor called the plateau. In ﬁgure 1 we observe

these features in SYK. While the early time decay depends on the speciﬁc system, the

ramp and plateau should be universal features of quantum chaotic systems. The ramp is

characteristic of spectral rigidity: the long-range logarithmic repulsion of eigenvalues. The

anticorrleation of eigenvalues causes the linear increase in the form factor. At late times,

or at energy scales smaller than the mean spacing, the form factor reaches a plateau as

degeneracies are rare and neighboring eigenvalues repel in chaotic systems.

SYK form factor and GUE. Recently, [27] studied the form factor in SYK and found

agreement with random matrix theory, showing analytically and numerically the aspects

of the dip, ramp, and plateau of SYK agree with those of the Gaussian unitary ensemble

– 4 –

JHEP05(2018)202

Slope

Dip

Ramp

Plateau

0.01 1 100

-5

-4

0.001

0.010

0.100

SYK form factor

Ramp

Plateau

0.01 1 100

-5

-4

0.001

0.010

0.100

SYK connected form factor

Figure 1. The 2-point spectral form factor and its connected component for SYK with N = 24

Majoranas at inverse temperature β = 1, computed for 800 realizations of disorder. We observe the

slope, dip, ramp, and plateau behaviors.

(GUE), an ensemble of L × L random Hermitian matrices. We will avoid explicitly in-

troducing and deﬁning the original Majorana, instead simply mentioning a few details to

better frame the discussion of the model’s supersymmetric extension.

The emergent reparamentrization invariance of SYK at strongly-coupled is broken

spontaneously and explicitly at low-energies, yielding an eﬀective description in terms of

the Schwarzian derivative [1, 3]. The 1-loop partition function of the Schwarzian theory

Sch

1-loop

∼ e

cN/2β

/β

3/2

, can be analytically continued to β + it to study the form factor of

SYK. At early times, R

(t, β) is dominated by the disconnected piece which gives a 1/t

power law decay, normalized by its initial value we have

hZ(β, t)Z

∗

(β, t)i

hZ(β)i

−cN/β

, (2.5)

for times greater than t &

√

N when the time dependence in the exponent disappears and

where c is the speciﬁc heat of the theory. To isolate this contribution, [27] considered a

special limit (a ‘triple scaled’ limit) where only the Schwarzian contributes. Moreover, [33]

showed that the Schwarzian theory is 1-loop exact and recieves no higher-order corrections,

indicating that the power-law decay predicted by the Schwarzian should dominate the

disconnected form factor for long times.

This power law decay is simply the Laplace

transform of the statement that the spectrum has a square-root edge

ρ(E) ∼ sinh

√

2cEN . (2.6)

Knowing the free energy in the large N limit, we can also show that the form factor of

SYK transitions to a ramp at a dip time t

∼ e

, growing linearly until a plateau time

of t

∼ e

+cN/2β

, where s

is the zero-temperature entropy density.

Many of these features of the SYK form factor agree with the universal predictions

from GUE. The form factor for GUE has been studied extensively in the random matrix

For more on solving the Schwarzian theory, see [34, 35].

As discussed in [3]. The spectral density of SYK has been further studied in [27, 36, 37].

– 5 –

剩余25页未读，继续阅读

weixin_38565818

粉丝: 3
资源: 956

超对称SYK模型中的混沌与随机矩阵分析

N $$ \ mathcal {N} $$ = 0、1和2超对称的SYK模型的完全随机矩阵分类

类超对称SYK张量模型

超对称SYK模型的全局对称性与混沌行为

超对称SYK模型：双局部集体超场与超矩阵解析

量子混沌和全息张量模型

全局对称性SYK模型与类SYK张量模型的强耦合解析

GUE随机矩阵中的RSB： wormhole网络模型的微观解析

平面矩阵量子力学与SYK模型的相变研究

量子混沌与全息张量模型的研究

Pytorch版代码幻灯片.zip

最新资源