卡尔曼滤波详解：从基础到应用

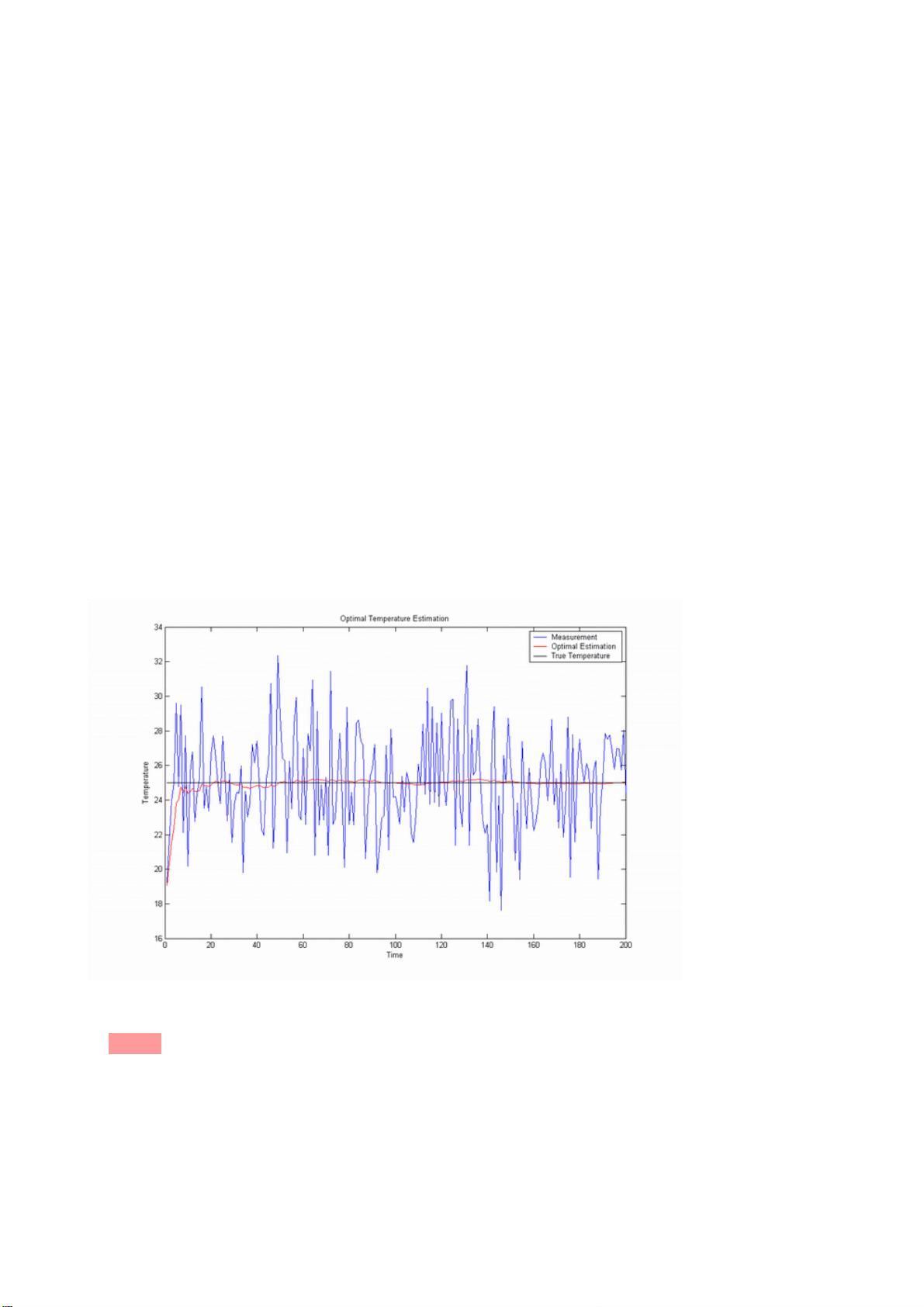
"卡尔曼滤波学习及应用" 卡尔曼滤波是一种统计滤波技术，由匈牙利数学家鲁道夫·艾米尔·卡尔曼在1960年提出，广泛应用于信号处理、控制理论、导航系统等领域。该滤波器以最优的方式融合了先验信息（预测）和观测信息，通过递归算法更新状态估计，从而得到更准确的系统状态。 1.1 关于卡尔曼滤波 卡尔曼滤波器基于最小均方误差准则，目的是在存在噪声的情况下，提供对动态系统状态的最佳线性估计。它适用于处理随机过程，如布朗运动或高斯白噪声，这些随机过程在实际应用中常常伴随着测量和系统模型的不确定性。 1.2 卡尔曼滤波器的举例说明 通常，卡尔曼滤波器的运作可以简化为一个追车问题：假设我们有一个车辆，其真实位置未知，只能通过有噪声的传感器获取不准确的位置信息。卡尔曼滤波器将根据上一时刻的估计位置和当前的观测，通过一组数学公式（预测和更新步骤）来不断校正车辆位置的估计。 1.3 卡尔曼滤波器算法 卡尔曼滤波器的核心算法包括预测（Predict）和更新（Update）两个阶段： - 预测阶段：根据系统的动态模型（状态转移矩阵）和控制输入，预测下一时刻的状态。 - 更新阶段：结合实际观测值，利用观测模型校正预测状态，得到最优的估计。 1.4 简单例子 在一个简单的1D平移系统中，状态变量为位置和速度，卡尔曼滤波器会估计出位置，同时考虑速度的变化，以减小测量噪声的影响。 2. 卡尔曼滤波的实现 - 基本假设：系统是线性的，噪声是零均值的高斯分布，且系统和观测模型是独立的。 - 基本公式：包括状态转移方程、观测方程、预测和更新步骤的矩阵表达式。 - 参数估计和调整：根据系统特性调整滤波器的参数，如协方差矩阵，以优化滤波性能。 - 初始化：正确设置初始状态和协方差矩阵，对滤波器的性能有很大影响。 3. 扩展卡尔曼滤波 当系统非线性时，可以通过泰勒级数展开线性化，形成扩展卡尔曼滤波。虽然线性化可能引入误差，但在许多情况下仍能提供良好的结果。 4. 卡尔曼滤波的相关知识 - 线性系统：卡尔曼滤波的基础，但实际应用中系统往往是非线性的。 - 泰勒级数展开：用于将非线性函数近似为线性函数，以便应用卡尔曼滤波。 - 雅可比矩阵：线性化的关键工具，描述非线性函数的局部线性变化。 5. 卡尔曼滤波应用 卡尔曼滤波在众多领域有广泛的应用，包括但不限于： - 机器人导航：融合GPS、陀螺仪和加速度计的数据，提供精确的定位信息。 - 控制系统：优化控制策略，如飞行控制系统。 - 传感器数据融合：提高多个传感器的测量精度。 - 军事应用：雷达系统和导弹追踪。 - 计算机视觉：头脸识别、图像分割和边缘检测等。 了解并掌握卡尔曼滤波，对于理解和解决复杂系统中的数据处理问题至关重要，它不仅是一个理论概念，更是实践中的强大工具。