数据结构八大排序算法详解

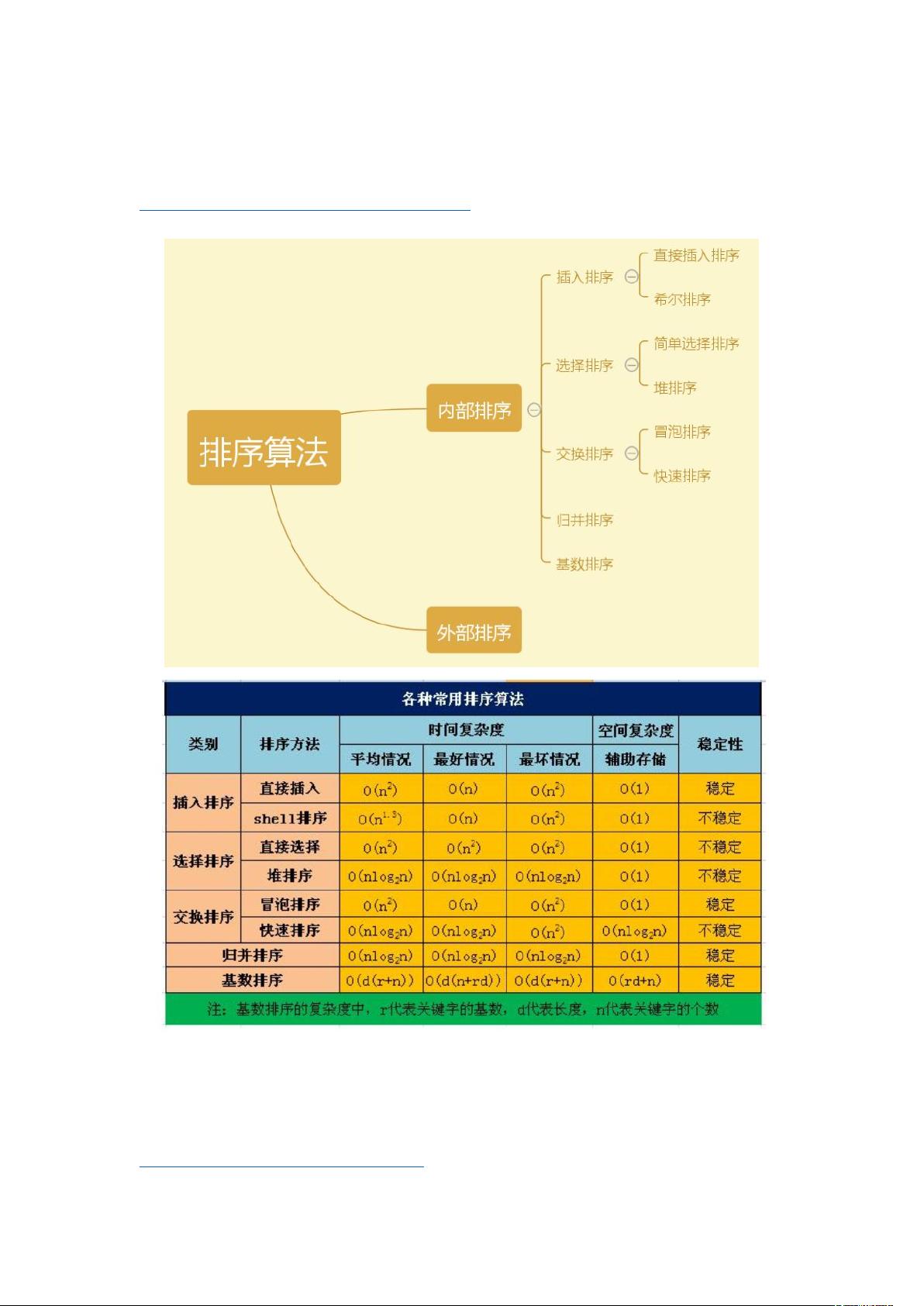
"排序算法总结，包括数据结构中常见的八大排序算法：直接插入排序、希尔排序、直接选择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。此外，还提及了外部排序的基本概念。" 1. 直接插入排序：这种排序算法的工作原理类似于玩扑克牌时整理手牌的过程。它将未排序的元素逐个与已排序的部分进行比较，并找到合适的位置插入。在最好的情况下，如果输入已经是有序的，直接插入排序的时间复杂度为O(n)。 2. 希尔排序：由Donald Shell提出，是一种改进的插入排序。希尔排序通过将数组分成若干子序列来减少元素之间的比较次数，然后逐步缩小子序列的间隔，最终达到完全排序的状态。其效率通常优于直接插入排序，但具体时间复杂度难以精确计算。 3. 直接选择排序：它每次从未排序的元素中找出最小（或最大）的元素，与第一个未排序的元素交换位置。这个过程重复n-1次，直到所有元素都有序。直接选择排序的时间复杂度为O(n^2)，并不适合处理大规模数据。 4. 堆排序：堆排序利用了堆这种数据结构。首先，将无序的数组构建成一个大顶堆（或小顶堆），然后将堆顶元素与末尾元素交换，去掉最后一个元素（即最大元素）。接着，对剩余元素重新调整成堆，再次交换堆顶和末尾，如此反复进行。堆排序的平均时间复杂度为O(nlogn)。 5. 冒泡排序：通过不断交换相邻的逆序元素来实现排序。每一轮比较后，最大的元素会被“冒泡”到数组的末尾。冒泡排序的时间复杂度最坏为O(n^2)，但在部分有序的情况下，效率较高。 6. 快速排序：由C.A.R. Hoare提出的经典排序算法，采用分治策略。选取一个“基准”元素，将数组分为比基准小和大的两部分，然后分别对这两部分递归地进行快速排序。快速排序的平均时间复杂度为O(nlogn)，最坏情况下为O(n^2)。 7. 归并排序：也是基于分治的算法。它将数组分成两半，分别进行排序，然后将两个有序的部分合并成一个大的有序数组。归并排序保证了稳定性，时间复杂度始终为O(nlogn)。 8. 基数排序：基数排序是根据数字的位数来进行的排序，从低位到高位依次处理。它将数字按位划分到不同的“桶”中，然后收集回原顺序。基数排序是稳定的，且在特定条件下，如基数较大时，效率较高，时间复杂度为O(nlog(r)m)，其中r为基数，m为桶的数量。 9. 外部排序：当数据量过大无法全部装入内存时，需要借助外部存储进行排序。外部排序通常涉及多路归并等步骤，先对小部分数据进行内部排序，然后逐步合并，直到完成整个数据集的排序。 这些排序算法各有优劣，适用场景不同，理解和掌握它们有助于解决各种排序问题，提高编程能力。