逻辑代数基础：布尔代数与数字电路设计入门

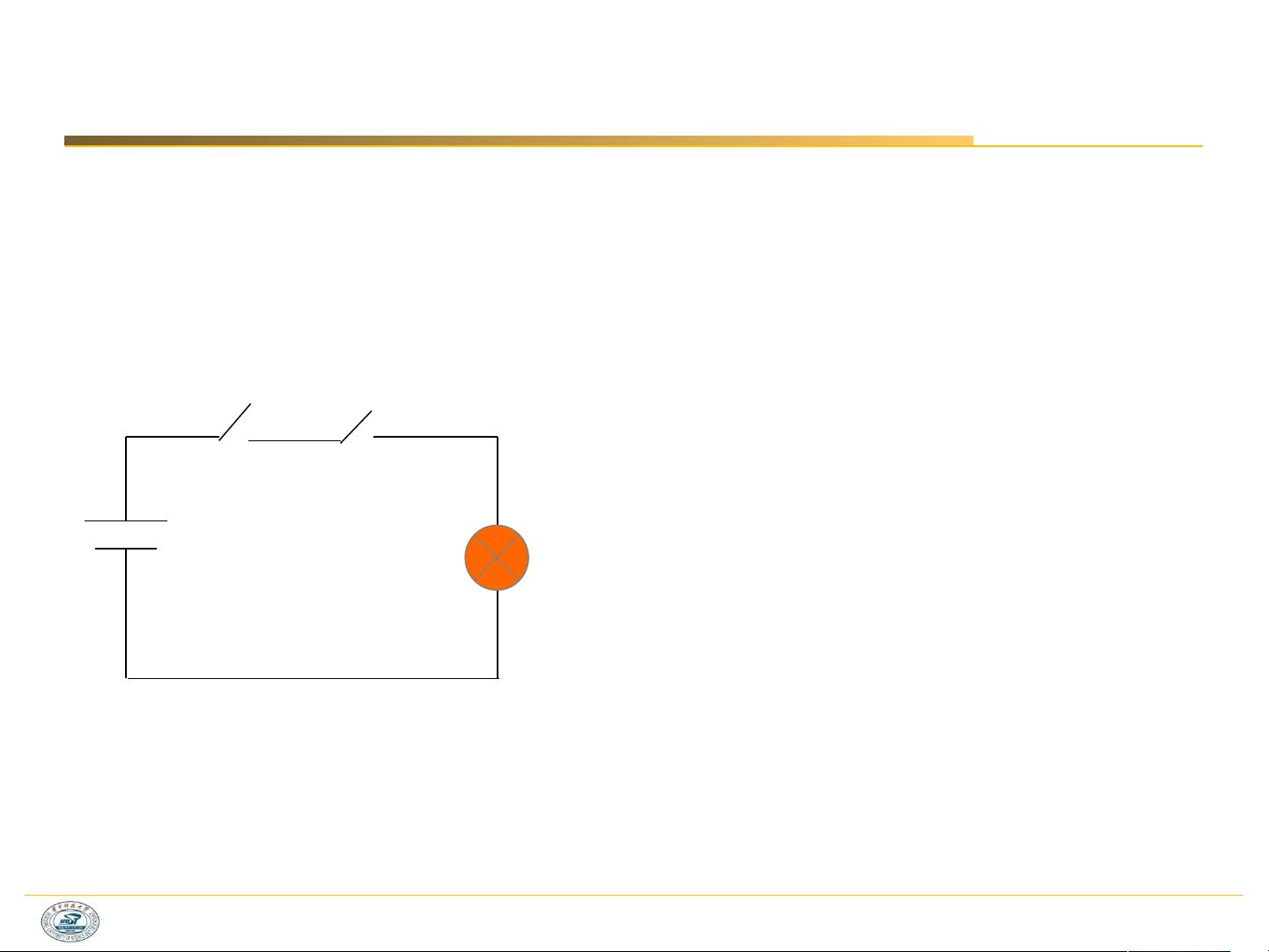
华中科技大学数字逻辑课件的第一章主要讲解逻辑代数的基础，这一章节对于理解数字电路与逻辑设计至关重要。逻辑代数起源于1847年英国数学家乔治·布尔的贡献，他提出了一种数学方法来表示命题的逻辑结构，发展出了布尔代数，这是一种将形式逻辑转化为代数演算的重要工具。1938年，克劳德·香农将布尔代数应用到电信工程领域，尤其是电话继电器的开关电路，形成了后来被称为逻辑代数的理论体系。 逻辑代数的基本框架包括一个逻辑变量集合K，常数0和1，以及“或”（+）、“与”（·）和“非”（-）这三种基本运算。这个代数系统遵循一系列公理，如交换律、结合律、分配律、0-1律和互补律，这些公理构成了逻辑代数的基础，确保了代数运算的正确性和一致性。 在逻辑代数中，变量是代表可以变化的量，但它们仅取两种可能的值：0或1。这些值被赋予特定的含义，0通常代表假或非，1代表真或是。逻辑运算包括： 1. “或”运算：当满足某事件的多个条件中有一个或多个成立时，事件就被认为是真的。这是一种“或”关系，表示只要有其中一个条件为真，结果就为真。 2. “与”运算：所有条件都必须同时为真，事件才被认为是真实的。“与”运算强调条件的全部满足。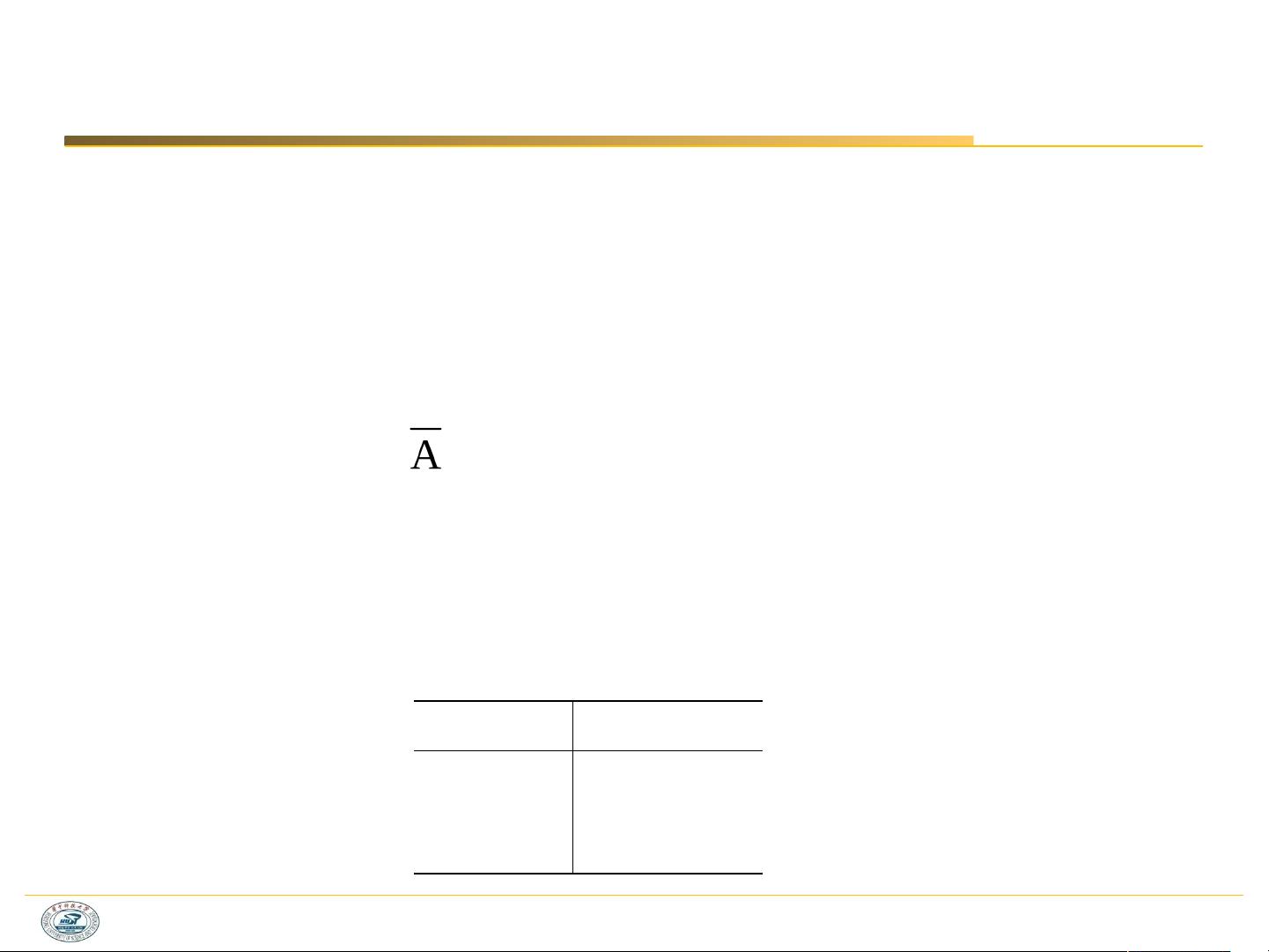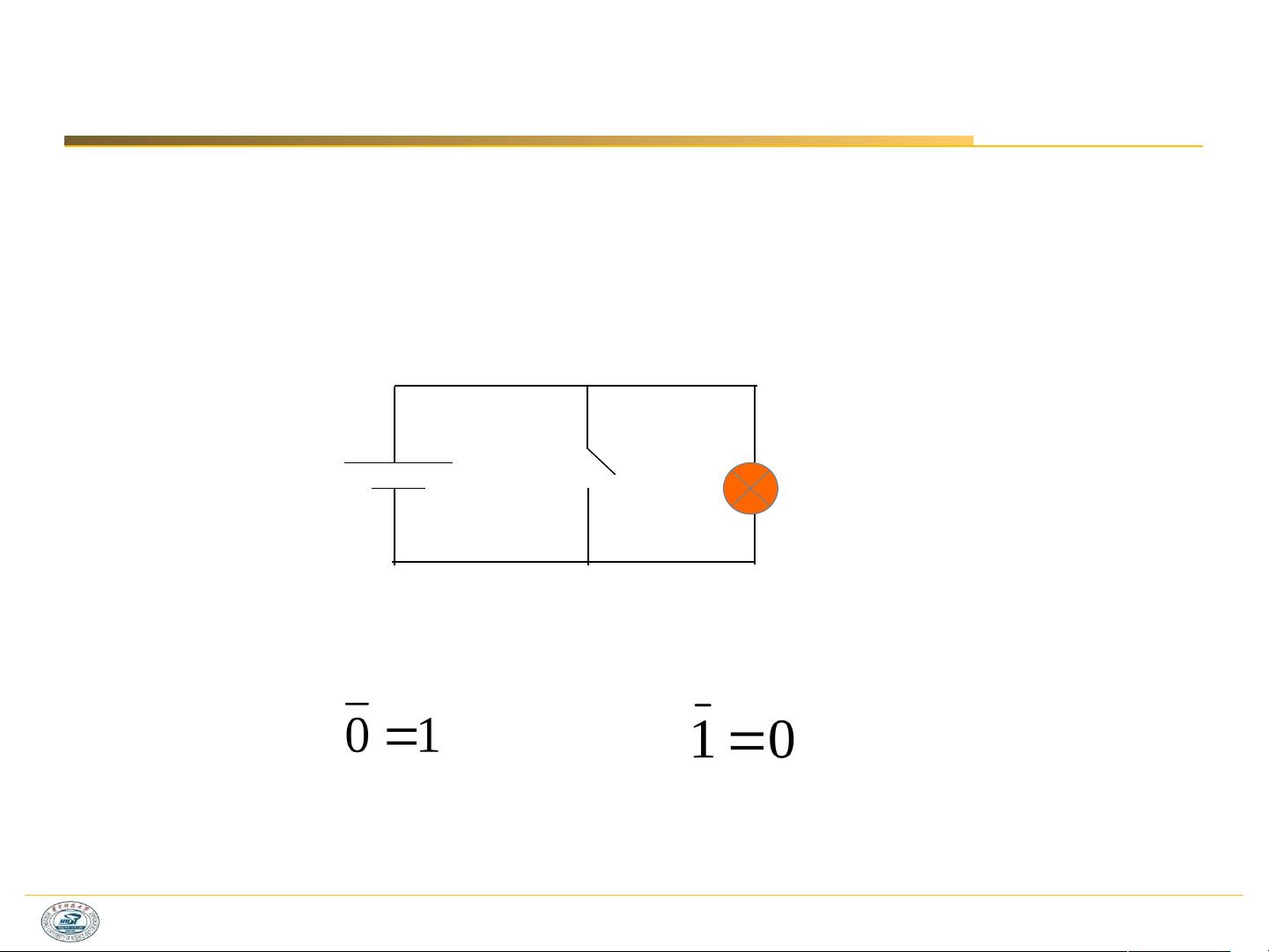 3. “非”运算（否定）：对一个逻辑变量进行取反操作，如果原变量为0，则结果为1，反之亦然，表示相反的状态。 通过逻辑函数的表示形式（如真值表、表达式等），可以对电路进行设计和分析。逻辑函数的化简是设计过程中必不可少的步骤，它涉及到简化逻辑表达式，降低电路复杂度，提高效率。理解并掌握这些基本概念和运算规则，是进行数字电路设计和分析的基础。 本章内容为学习者提供了一个坚实的基础，让他们能够运用逻辑代数工具来分析、设计和优化数字电路，是数字电路与逻辑设计课程中的核心知识点。