回溯法解决子集和数问题-马丙鹏《计算机算法设计与分析》第六章

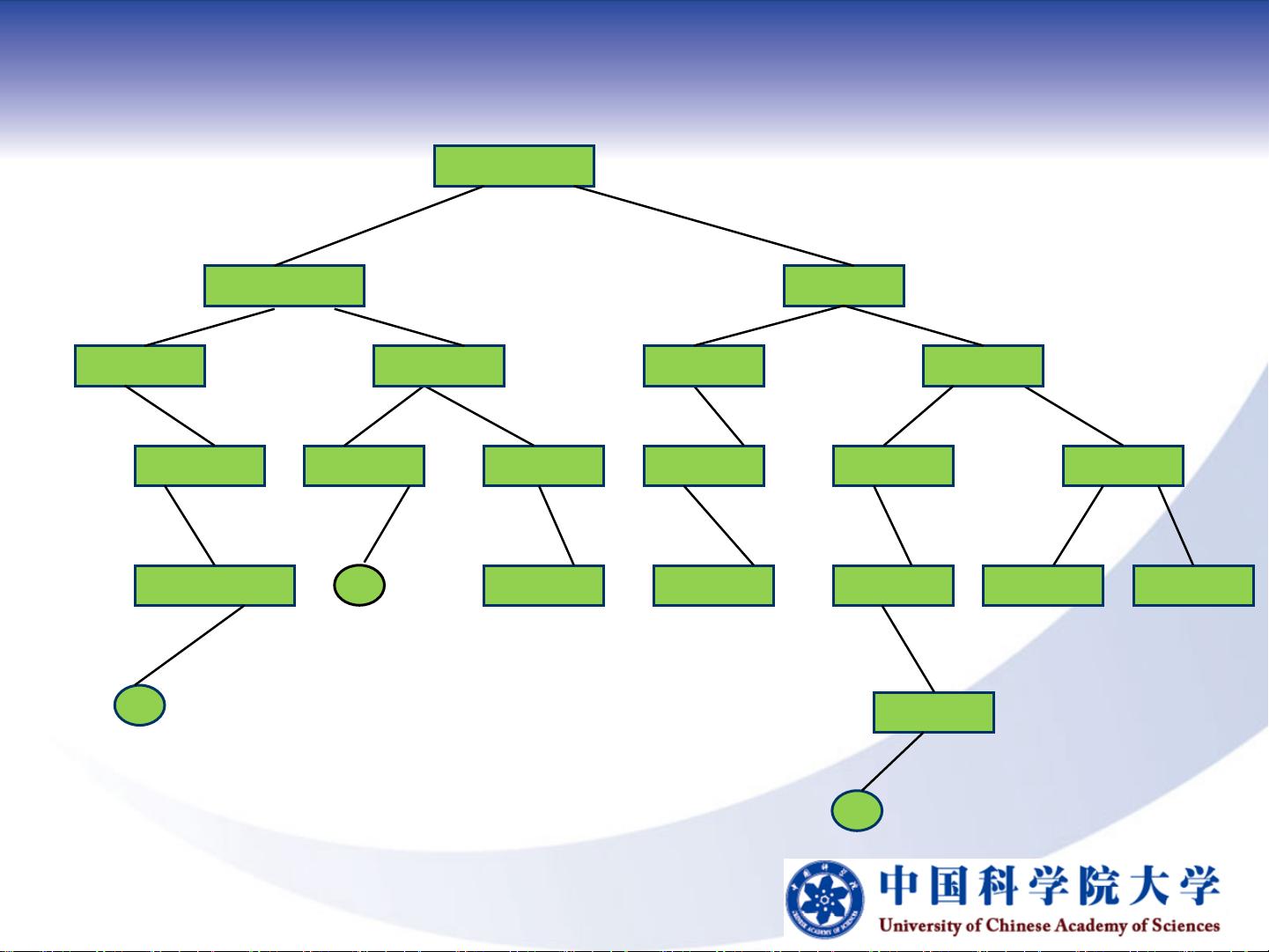
回溯法是一种常用的求解组合优化问题的方法，它通过构建状态空间树，从而依次生成问题的所有可能解，然后再根据问题的约束条件进行剪枝，找到最优解或满足条件的解。在回溯法中，我们会将问题分解为子问题，并在每一步中选择一个可行的决策，然后递归地继续求解下一个子问题。如果发现当前选择的路径不满足约束条件，则回溯到上一步，重新选择决策，直到找到问题的解或者全部搜索完毕。 在第六章中，我们介绍了回溯法的一般方法，并且以几个具体的问题为例，展示了如何应用回溯法来解决这些问题。首先介绍了经典的8皇后问题，该问题需要在一个8×8的棋盘上摆放8个皇后，要求每个皇后所在的行、列和对角线上都不能有其他皇后。通过回溯法，我们可以逐个地尝试在每一行放置皇后，并根据约束条件进行剪枝，从而找到所有的解。 接着，我们介绍了子集和数问题，该问题需要找到一个集合中所有满足条件的子集，使得子集中的元素之和等于给定的正整数M。通过回溯法，我们可以构建一个状态空间树，每个节点表示一个候选解元组，根据约束条件进行剪枝，从而找到满足条件的所有解。 然后，我们介绍了图的着色问题，该问题需要在给定的无向图中为每个顶点选择一个颜色，要求相邻的顶点不能有相同的颜色。通过回溯法，我们可以逐个地尝试为每个顶点选择颜色，并根据约束条件进行剪枝，从而找到图的着色方案。 最后，我们介绍了0/1背包问题，该问题需要在一组物品中选择一些物品放入背包中，使得物品的总重量不超过背包的容量，并且物品的总价值最大。通过回溯法，我们可以逐个地尝试选择物品，并根据约束条件进行剪枝，从而找到最优的放置方案。 总之，回溯法是一种生成所有可能解并逐步筛选的求解组合优化问题的方法。它的核心思想是构建状态空间树，并通过剪枝操作来减小搜索空间，从而找到最优解或满足条件的解。在实际应用中，我们可以根据具体问题的特点来设计适当的约束条件和剪枝策略，以提高算法的效率和求解能力。通过掌握回溯法的基本原理和应用技巧，我们可以更好地解决各种组合优化问题，提高算法设计与分析的能力。