理解矩阵特征值分解与奇异值分解

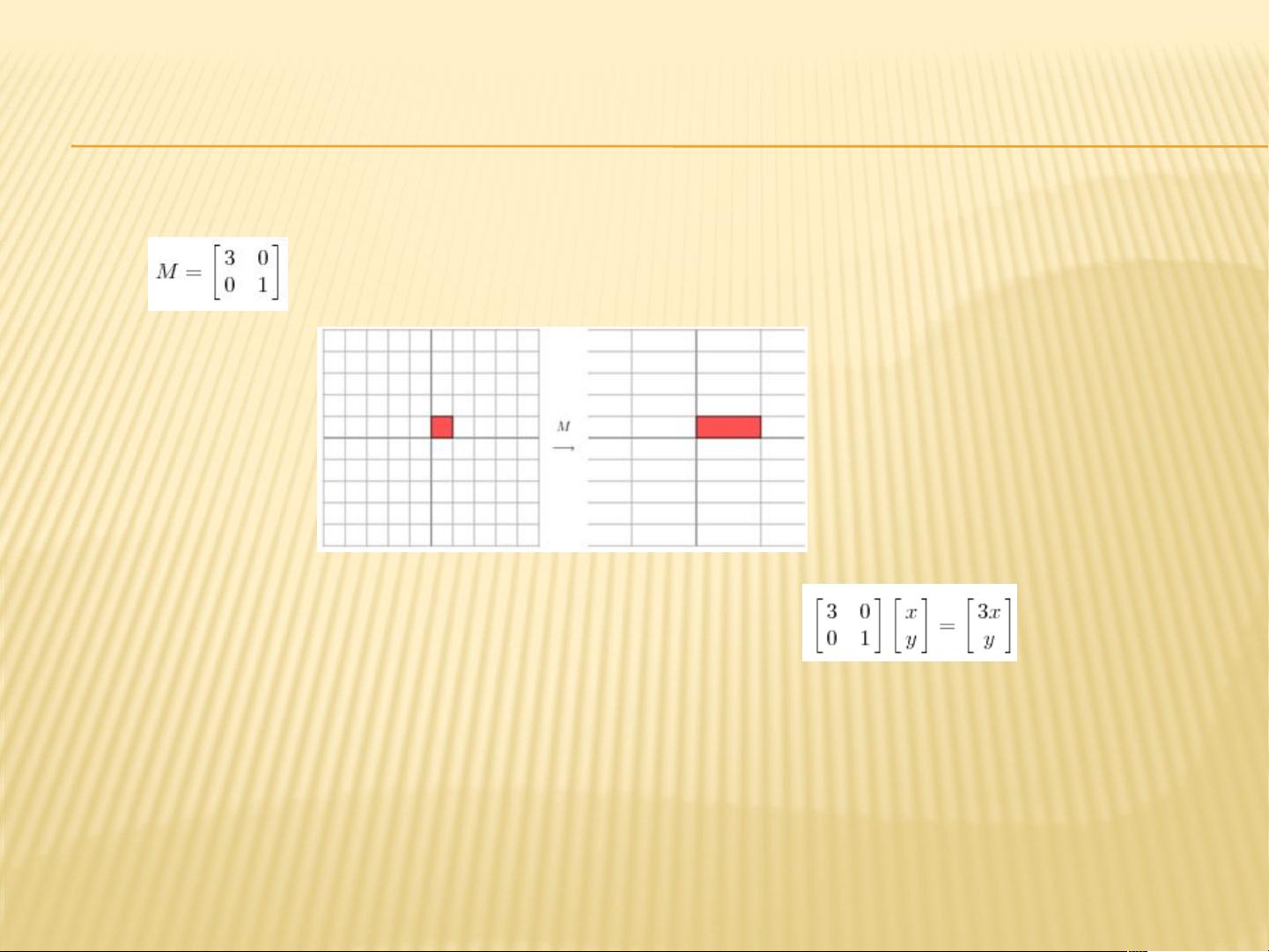
"本文介绍了矩阵的特征值分解与奇异值分解，这两种分解方法在理解和分析矩阵性质方面具有重要意义，尤其适用于入门学习者。特征值分解关注于矩阵对向量的伸缩变换，而奇异值分解则扩展了这一概念，适用于非方阵的情况，具有更广泛的应用场景。" 在矩阵理论中，特征值分解和奇异值分解是两种重要的矩阵运算，它们能够揭示矩阵的内在结构和特性。特征值分解主要应用于方阵，它揭示了矩阵在变换过程中的主要行为。特征向量是矩阵作用下保持方向不变但仅改变长度的向量，而特征值则对应于这个长度的缩放因子。在几何意义上，特征向量代表了矩阵变换的主要方向，特征值则度量了沿着这些方向的伸缩程度。 特征值分解的数学表达式为 \( A = Q \Sigma Q^T \)，其中 \( A \) 是一个方阵，\( Q \) 包含了所有特征向量作为列，\( \Sigma \) 是一个对角矩阵，对角线上的元素即为特征值。通过这种方式，矩阵 \( A \) 可以被分解为一组正交基（由 \( Q \) 的列向量构成）以及它们对应的伸缩因子（对角矩阵 \( \Sigma \) 的元素）。这种分解有助于识别矩阵的主要特征，尤其是在数据分析和机器学习中，用于主成分分析（PCA）等降维技术。 然而，现实世界中的数据常常表现为非方阵，这时特征值分解就无法直接应用。奇异值分解（SVD）解决了这个问题，它能够对任何实数矩阵进行分解。SVD 将矩阵 \( A \) 表示为 \( A = U \Sigma V^T \)，其中 \( U \) 和 \( V \) 是正交矩阵，\( \Sigma \) 是一个对角矩阵，其对角线上的元素称为奇异值。奇异值类似于特征值，但它们不仅存在于方阵中，而且可以捕捉非方阵的全部信息。奇异值分解在图像处理、推荐系统和信号处理等领域有着广泛应用。 奇异值分解的优越性在于，即使在矩阵不是方阵的情况下，也能提供一种有效的数据压缩手段。通过选取最大的几个奇异值及其对应的左奇异向量和右奇异向量，可以近似重构原始矩阵，从而实现数据降噪或减少计算复杂度。 总结来说，特征值分解和奇异值分解是理解矩阵变换本质的重要工具。特征值分解用于方阵，揭示矩阵变换的主要方向和伸缩比例，而奇异值分解则扩展到非方阵，同样捕获主要特征并适用于更广泛的数据类型。这两种方法在数据分析、机器学习和工程问题中都有着不可忽视的作用。