图像去噪与模糊角度估计：均值滤波的应用

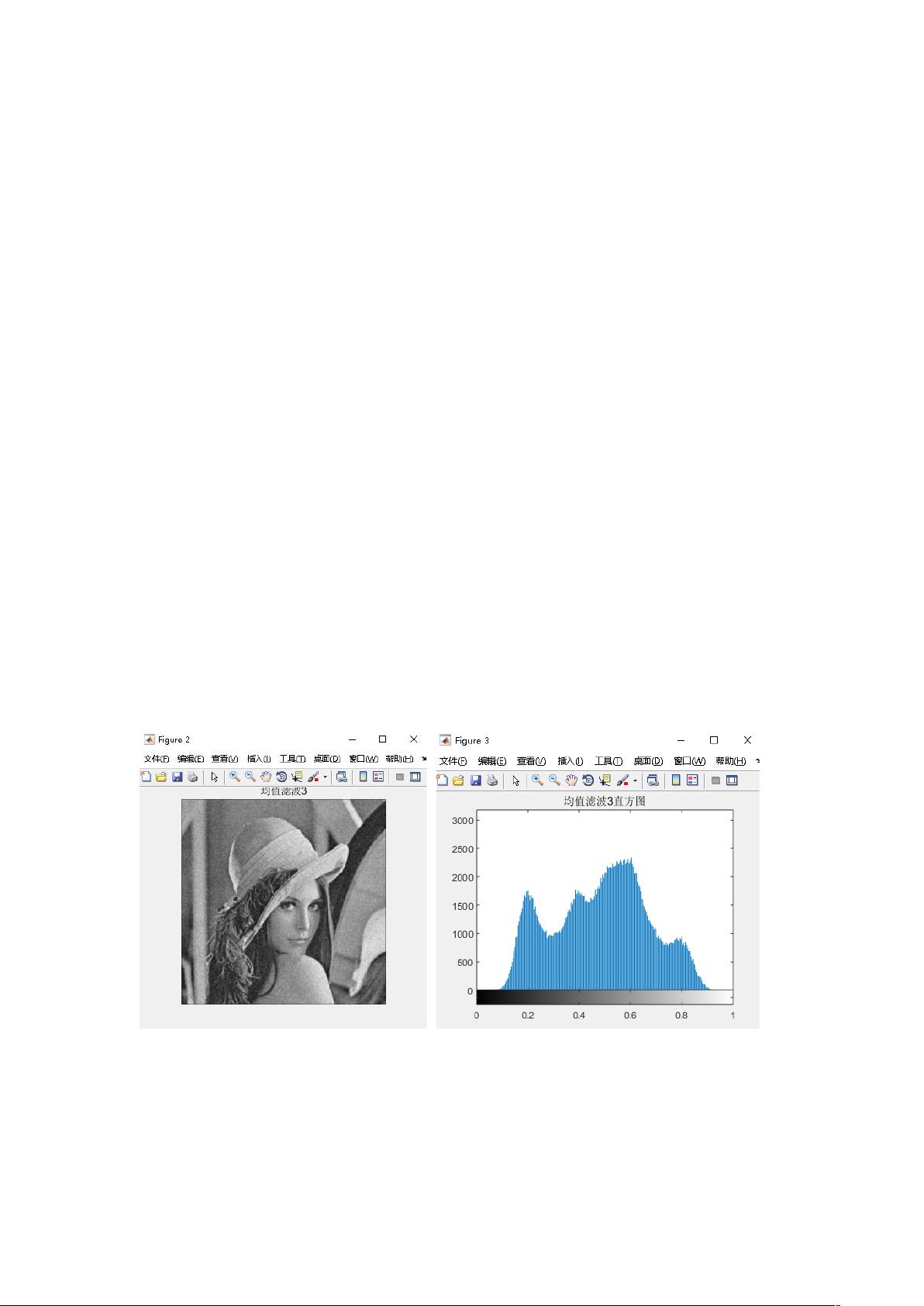
"图像处理与模糊角度估计" 在图像处理领域，去噪是至关重要的一步，尤其是在处理模糊图像时。本文主要探讨了两种常见的去噪方法：均值滤波和维纳滤波，并涉及模糊角度的估计。对于均值滤波，这是一种线性滤波技术，通过计算像素邻域内的平均值来替代目标像素的值，以此消除噪声。然而，这种方法会破坏图像的边缘和细节，导致图像模糊。 均值滤波器有多种变体，包括算术均值滤波、几何均值滤波、谐波均值滤波和逆谐波均值滤波。其中，几何均值滤波被认为在保持图像细节方面优于算术均值滤波，但平滑效果略逊一筹。在实验分析中，以"lena_ny.jpg"为例，展示了原始图像及其直方图，通过直方图可以初步判断图像中的噪声类型并评估降噪效果。 均值滤波的实现通常使用`filter2`函数，配合`fspecial`函数创建不同大小的平均滤波模板。例如，使用3x3、5x5、7x7和9x9的模板对图像进行滤波，可以观察到随着模板尺寸增大，降噪效果更明显，但图像的模糊程度也会增加。 接下来，对于模糊角度的估计，这通常涉及到图像的频域分析。维纳滤波是一种用于恢复图像的频率域方法，它基于信号和噪声的功率谱来恢复图像。在模糊图像中，模糊角度通常指的是图像失真的方向，可以通过分析图像的傅里叶变换特性来估计。维纳滤波器旨在最小化重构图像与原始图像之间的均方误差，同时尽可能减少噪声的影响。 在实际应用中，需要首先对图像进行傅里叶变换，然后应用维纳滤波器公式，最后进行逆傅里叶变换以恢复图像。这个过程可以通过MATLAB等工具实现，其中`fft2`用于二维傅里叶变换，`ifft2`用于逆变换。模糊角度的估计可能涉及对滤波器的旋转，以适应不同的模糊方向。 图像处理中的去噪和模糊角度估计是两个相互关联但又独立的步骤。通过均值滤波可以去除大部分噪声，但可能导致图像细节损失；而模糊角度的估计则有助于理解图像的失真情况，为恢复清晰图像提供关键信息。在实际操作中，往往需要结合多种方法和技术，如结合其他滤波器（如中值滤波、高斯滤波）和更复杂的图像恢复算法，以达到最佳的图像处理效果。