移轴的子空间迭代法及其在广义特征值问题中的应用-李萌大作业报告1

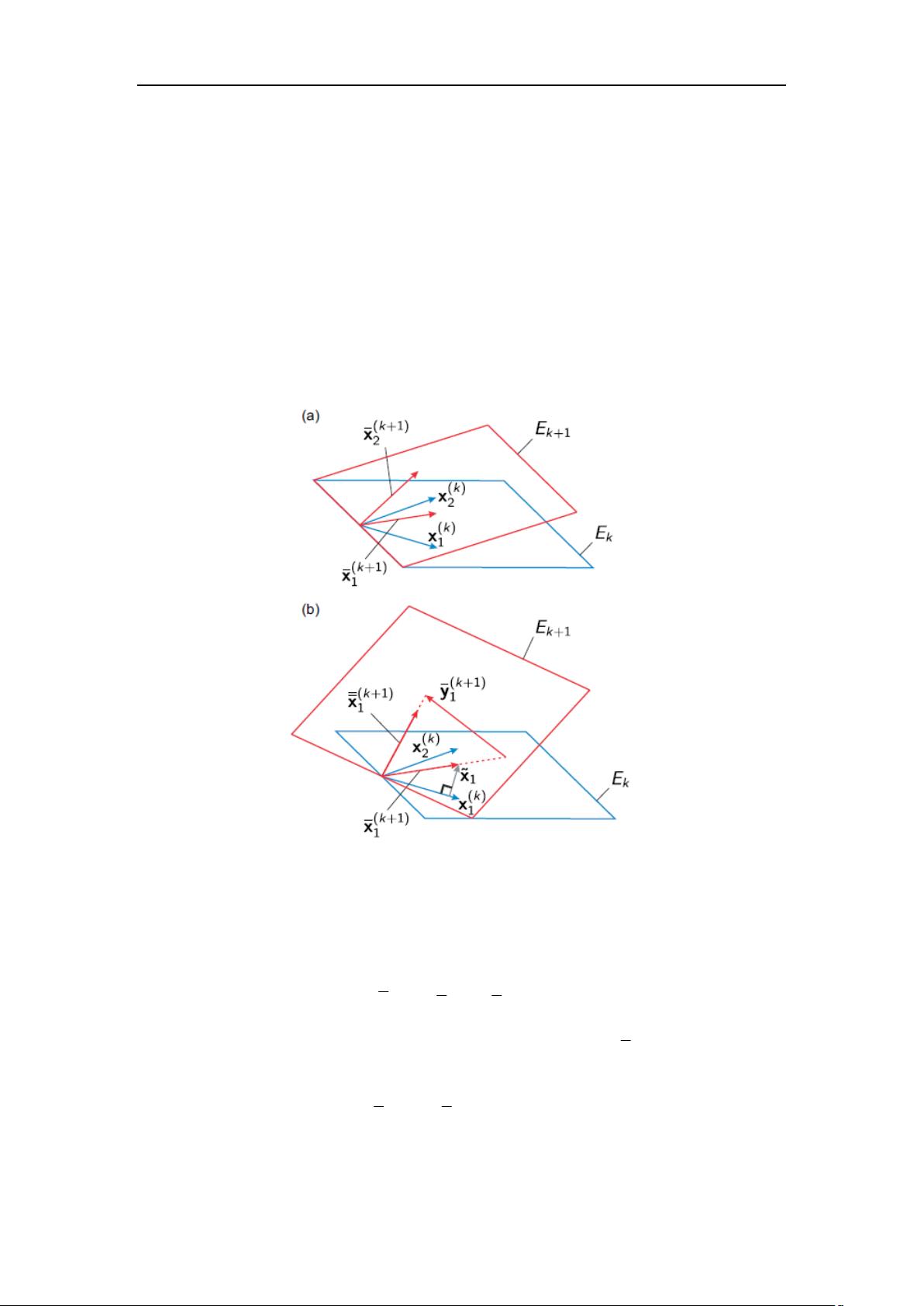
本报告主要介绍了引入移轴的子空间迭代法，并对其进行了详细的讨论和分析。首先，我们给出了公式引入移轴量后，广义特征值问题的变化，然后在1.1.1小节中对子空间迭代公式进行了相应的修改。在整个报告中，我们主要讨论了移轴的子空间迭代法的相关文献调研、经典的子空间迭代法、新型变带宽存储方案、高效LDLT分解算法以及旋转向量等内容。 在文献调研方面，我们对引入移轴的子空间迭代法做了详细的调研，总结了现有的研究成果，并指出了存在的问题和不足之处。在经典的子空间迭代法部分，我们对传统的子空间迭代法进行了介绍，包括其基本原理和算法流程，以及在实际应用中的一些局限性和不足之处。在引入移轴的子空间迭代法部分，我们详细说明了引入移轴量后的广义特征值问题的变化，以及如何相应地修改子空间迭代公式，从而提高算法的收敛速度和稳定性。在新型变带宽存储方案和高效LDLT分解算法部分，我们介绍了这两种算法在解决大规模稀疏线性方程组和特征值问题中的重要作用，以及它们的优点和特点。最后，在旋转向量部分，我们简要介绍了旋转向量在计算机图形学和机器人运动学中的应用。 通过本报告的研究和分析，我们得出了以下结论：引入移轴的子空间迭代法在求解广义特征值问题方面具有一定的优势，特别是在提高算法的收敛速度和稳定性方面有显著的改进。同时，新型变带宽存储方案和高效LDLT分解算法在解决大规模稀疏线性方程组和特征值问题中具有重要的应用前景，可以有效地提高求解问题的效率和准确性。此外，旋转向量作为一种重要的数学工具，在计算机图形学和机器人运动学等领域有着广泛的应用前景。 综上所述，本报告对引入移轴的子空间迭代法进行了深入的研究和分析，对其在求解广义特征值问题中的优势和应用前景进行了全面的展示，为相关领域的研究工作提供了重要的参考和借鉴。同时，本报告也为相关算法和技术的进一步改进和完善提供了一定的思路和方向。希望本报告的研究成果能够对相关领域的学术研究和工程应用产生一定的推动作用，为促进科技进步和社会发展做出应有的贡献。