17
Graph Representations
Xavier Bresson 17
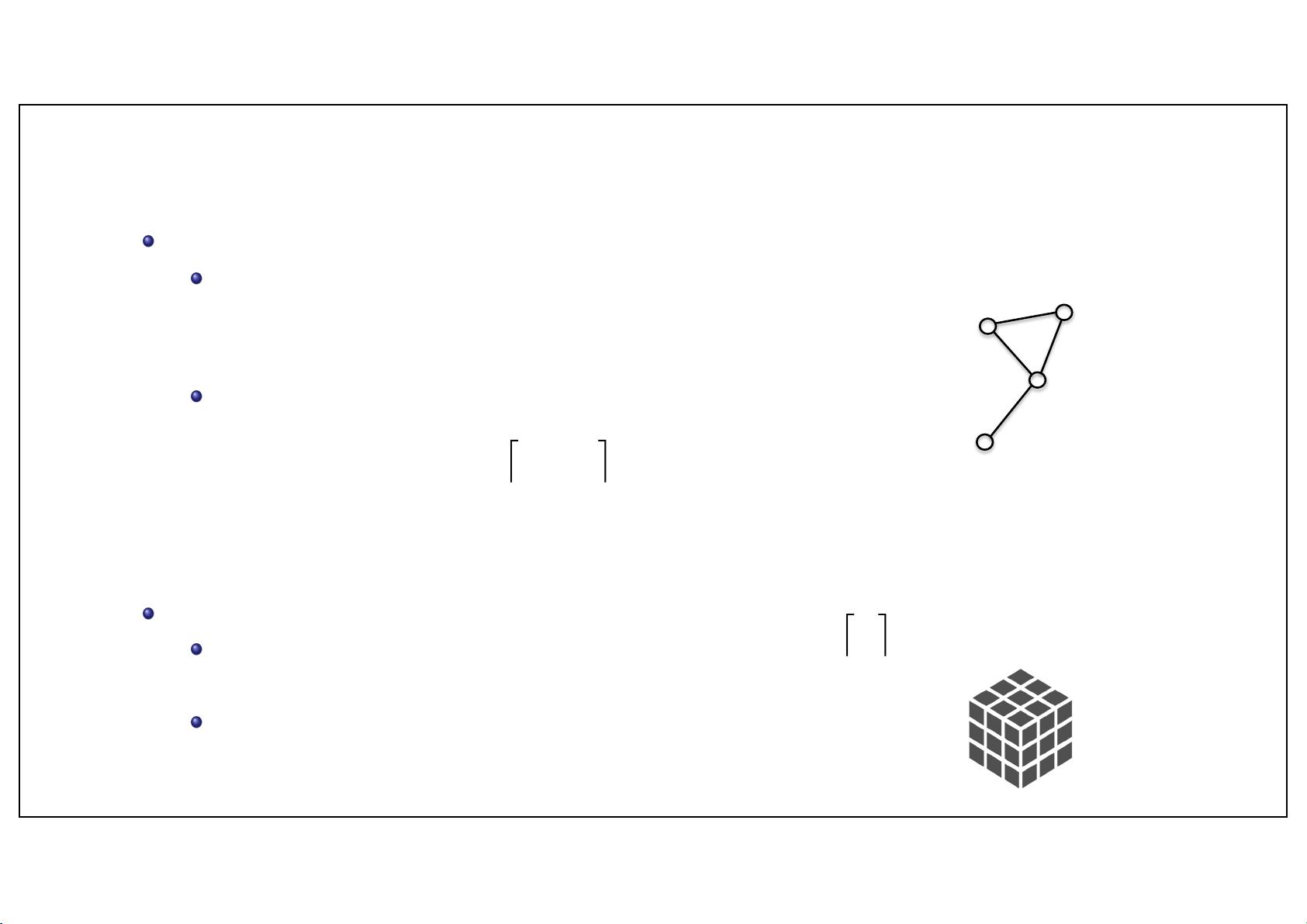
Graphs are rank-
2
tensors. They can be represented as
List of edges (short lists for sparse graphs):
E
=
[ {1,2}, {1,3}, {2,3}, {3,4} ]
Matrix (dense tensor):
Other tensors :
Vectors (ordered and unordered sets) are rank-
1
tensors :
General tensors (s.a. 3D-MRIs or hyper-graphs) of rank-
m
:
index 1
index 4
index 3
index 2
<latexit sha1_base64="239FBV4Lx15Q0Pwecwy+zRLKQeE=">AAAB/XicbVDLSgMxFL1TX7W+xsfOTbAIFaTMFEE3QkFElxXsA9qhZNK0Dc1khiQj1KH4K25cKOLW/3Dn35hpZ6GtBwKHc+7lnhw/4kxpx/m2ckvLK6tr+fXCxubW9o69u9dQYSwJrZOQh7LlY0U5E7Sumea0FUmKA5/Tpj+6Sv3mA5WKheJejyPqBXggWJ8RrI3UtQ86AdZDgnlyM0GXqNQ4vT4pdO2iU3amQIvEzUgRMtS69lenF5I4oEITjpVqu06kvQRLzQink0InVjTCZIQHtG2owAFVXjJNP0HHRumhfijNExpN1d8bCQ6UGge+mUyzqnkvFf/z2rHuX3gJE1GsqSCzQ/2YIx2itArUY5ISzceGYCKZyYrIEEtMtCksLcGd//IiaVTKrlN2786K1UpWRx4O4QhK4MI5VOEWalAHAo/wDK/wZj1ZL9a79TEbzVnZzj78gfX5A94Dk3c=</latexit>
<latexit sha1_base64="239FBV4Lx15Q0Pwecwy+zRLKQeE=">AAAB/XicbVDLSgMxFL1TX7W+xsfOTbAIFaTMFEE3QkFElxXsA9qhZNK0Dc1khiQj1KH4K25cKOLW/3Dn35hpZ6GtBwKHc+7lnhw/4kxpx/m2ckvLK6tr+fXCxubW9o69u9dQYSwJrZOQh7LlY0U5E7Sumea0FUmKA5/Tpj+6Sv3mA5WKheJejyPqBXggWJ8RrI3UtQ86AdZDgnlyM0GXqNQ4vT4pdO2iU3amQIvEzUgRMtS69lenF5I4oEITjpVqu06kvQRLzQink0InVjTCZIQHtG2owAFVXjJNP0HHRumhfijNExpN1d8bCQ6UGge+mUyzqnkvFf/z2rHuX3gJE1GsqSCzQ/2YIx2itArUY5ISzceGYCKZyYrIEEtMtCksLcGd//IiaVTKrlN2786K1UpWRx4O4QhK4MI5VOEWalAHAo/wDK/wZj1ZL9a79TEbzVnZzj78gfX5A94Dk3c=</latexit>
<latexit sha1_base64="239FBV4Lx15Q0Pwecwy+zRLKQeE=">AAAB/XicbVDLSgMxFL1TX7W+xsfOTbAIFaTMFEE3QkFElxXsA9qhZNK0Dc1khiQj1KH4K25cKOLW/3Dn35hpZ6GtBwKHc+7lnhw/4kxpx/m2ckvLK6tr+fXCxubW9o69u9dQYSwJrZOQh7LlY0U5E7Sumea0FUmKA5/Tpj+6Sv3mA5WKheJejyPqBXggWJ8RrI3UtQ86AdZDgnlyM0GXqNQ4vT4pdO2iU3amQIvEzUgRMtS69lenF5I4oEITjpVqu06kvQRLzQink0InVjTCZIQHtG2owAFVXjJNP0HHRumhfijNExpN1d8bCQ6UGge+mUyzqnkvFf/z2rHuX3gJE1GsqSCzQ/2YIx2itArUY5ISzceGYCKZyYrIEEtMtCksLcGd//IiaVTKrlN2786K1UpWRx4O4QhK4MI5VOEWalAHAo/wDK/wZj1ZL9a79TEbzVnZzj78gfX5A94Dk3c=</latexit>
<latexit sha1_base64="239FBV4Lx15Q0Pwecwy+zRLKQeE=">AAAB/XicbVDLSgMxFL1TX7W+xsfOTbAIFaTMFEE3QkFElxXsA9qhZNK0Dc1khiQj1KH4K25cKOLW/3Dn35hpZ6GtBwKHc+7lnhw/4kxpx/m2ckvLK6tr+fXCxubW9o69u9dQYSwJrZOQh7LlY0U5E7Sumea0FUmKA5/Tpj+6Sv3mA5WKheJejyPqBXggWJ8RrI3UtQ86AdZDgnlyM0GXqNQ4vT4pdO2iU3amQIvEzUgRMtS69lenF5I4oEITjpVqu06kvQRLzQink0InVjTCZIQHtG2owAFVXjJNP0HHRumhfijNExpN1d8bCQ6UGge+mUyzqnkvFf/z2rHuX3gJE1GsqSCzQ/2YIx2itArUY5ISzceGYCKZyYrIEEtMtCksLcGd//IiaVTKrlN2786K1UpWRx4O4QhK4MI5VOEWalAHAo/wDK/wZj1ZL9a79TEbzVnZzj78gfX5A94Dk3c=</latexit>
2 R
n
m
<latexit sha1_base64="z7CqSd7qrIzjKmZq9xLPmUXSFD8=">AAAB/XicbVDLSsNAFL3xWesrPnZugkVwVZIi6LLgxmUV+4AmLZPppB06MwkzE6GG4q+4caGIW//DnX/jpM1CWw8MHM65l3vmhAmjSrvut7Wyura+sVnaKm/v7O7t2weHLRWnEpMmjlksOyFShFFBmppqRjqJJIiHjLTD8XXutx+IVDQW93qSkICjoaARxUgbqW8f+1T4HOlRGGZ3014menxa7tsVt+rO4CwTryAVKNDo21/+IMYpJ0JjhpTqem6igwxJTTEj07KfKpIgPEZD0jVUIE5UkM3ST50zowycKJbmCe3M1N8bGeJKTXhoJvOgatHLxf+8bqqjqyCjIkk1EXh+KEqZo2Mnr8IZUEmwZhNDEJbUZHXwCEmEtSksL8Fb/PIyadWqnlv1bi8q9VpRRwlO4BTOwYNLqMMNNKAJGB7hGV7hzXqyXqx362M+umIVO0fwB9bnD59RlUM=</latexit>
<latexit sha1_base64="z7CqSd7qrIzjKmZq9xLPmUXSFD8=">AAAB/XicbVDLSsNAFL3xWesrPnZugkVwVZIi6LLgxmUV+4AmLZPppB06MwkzE6GG4q+4caGIW//DnX/jpM1CWw8MHM65l3vmhAmjSrvut7Wyura+sVnaKm/v7O7t2weHLRWnEpMmjlksOyFShFFBmppqRjqJJIiHjLTD8XXutx+IVDQW93qSkICjoaARxUgbqW8f+1T4HOlRGGZ3014menxa7tsVt+rO4CwTryAVKNDo21/+IMYpJ0JjhpTqem6igwxJTTEj07KfKpIgPEZD0jVUIE5UkM3ST50zowycKJbmCe3M1N8bGeJKTXhoJvOgatHLxf+8bqqjqyCjIkk1EXh+KEqZo2Mnr8IZUEmwZhNDEJbUZHXwCEmEtSksL8Fb/PIyadWqnlv1bi8q9VpRRwlO4BTOwYNLqMMNNKAJGB7hGV7hzXqyXqx362M+umIVO0fwB9bnD59RlUM=</latexit>
<latexit sha1_base64="z7CqSd7qrIzjKmZq9xLPmUXSFD8=">AAAB/XicbVDLSsNAFL3xWesrPnZugkVwVZIi6LLgxmUV+4AmLZPppB06MwkzE6GG4q+4caGIW//DnX/jpM1CWw8MHM65l3vmhAmjSrvut7Wyura+sVnaKm/v7O7t2weHLRWnEpMmjlksOyFShFFBmppqRjqJJIiHjLTD8XXutx+IVDQW93qSkICjoaARxUgbqW8f+1T4HOlRGGZ3014menxa7tsVt+rO4CwTryAVKNDo21/+IMYpJ0JjhpTqem6igwxJTTEj07KfKpIgPEZD0jVUIE5UkM3ST50zowycKJbmCe3M1N8bGeJKTXhoJvOgatHLxf+8bqqjqyCjIkk1EXh+KEqZo2Mnr8IZUEmwZhNDEJbUZHXwCEmEtSksL8Fb/PIyadWqnlv1bi8q9VpRRwlO4BTOwYNLqMMNNKAJGB7hGV7hzXqyXqx362M+umIVO0fwB9bnD59RlUM=</latexit>
<latexit sha1_base64="z7CqSd7qrIzjKmZq9xLPmUXSFD8=">AAAB/XicbVDLSsNAFL3xWesrPnZugkVwVZIi6LLgxmUV+4AmLZPppB06MwkzE6GG4q+4caGIW//DnX/jpM1CWw8MHM65l3vmhAmjSrvut7Wyura+sVnaKm/v7O7t2weHLRWnEpMmjlksOyFShFFBmppqRjqJJIiHjLTD8XXutx+IVDQW93qSkICjoaARxUgbqW8f+1T4HOlRGGZ3014menxa7tsVt+rO4CwTryAVKNDo21/+IMYpJ0JjhpTqem6igwxJTTEj07KfKpIgPEZD0jVUIE5UkM3ST50zowycKJbmCe3M1N8bGeJKTXhoJvOgatHLxf+8bqqjqyCjIkk1EXh+KEqZo2Mnr8IZUEmwZhNDEJbUZHXwCEmEtSksL8Fb/PIyadWqnlv1bi8q9VpRRwlO4BTOwYNLqMMNNKAJGB7hGV7hzXqyXqx362M+umIVO0fwB9bnD59RlUM=</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="hP+6LrUf2d3tZaldqaQQvEKMXyw=">AAAB2XicbZDNSgMxFIXv1L86Vq1rN8EiuCozbnQpuHFZwbZCO5RM5k4bmskMyR2hDH0BF25EfC93vo3pz0JbDwQ+zknIvSculLQUBN9ebWd3b/+gfugfNfzjk9Nmo2fz0gjsilzl5jnmFpXU2CVJCp8LgzyLFfbj6f0i77+gsTLXTzQrMMr4WMtUCk7O6oyaraAdLMW2IVxDC9YaNb+GSS7KDDUJxa0dhEFBUcUNSaFw7g9LiwUXUz7GgUPNM7RRtRxzzi6dk7A0N+5oYkv394uKZ9bOstjdzDhN7Ga2MP/LBiWlt1EldVESarH6KC0Vo5wtdmaJNChIzRxwYaSblYkJN1yQa8Z3HYSbG29D77odBu3wMYA6nMMFXEEIN3AHD9CBLghI4BXevYn35n2suqp569LO4I+8zx84xIo4</latexit>
<latexit sha1_base64="hnJ+4vLmYL7ONXRI/h4zSG5Blzo=">AAACJ3icbVBNT9tAFHyG0qYmlMCVywqExCmyubRHJC70FiqSIMUmWm+ek1XWa2v3GSmy/Jt66S+p1AMcihB/hHWSSuVjtCuNZnY1701SKGkpCO68jc0PWx8/tT772+2dL7udvfbA5qUR2Be5ys11wi0qqbFPkhReFwZ5ligcJvPzxh/eorEy11e0KDDO+FTLVApOThp3vkcKUxr5UYJTqStuDF/Ulaj9KPp3UE/Wuh8ZOZ1R7EdSRxmnWZJUP+qbSteM+ePOUdANlmBvSbgmR7BGb9z5HU1yUWaoSShu7SgMCopdFEmh0IWVFgsu5nyKI0c1z9DG1XLlmh07ZcLS3LiriS3V/39UPLN2kSXuZTOofe014nveqKT0W1xJXZSEWqyC0lIxylnTH5tIg4LUwhEujHSzMjHjhgtyLTclhK9XfksGp90w6IaXAbTgAA7hBEL4CmdwAT3og4Cf8Af+woP3y7v3Hld1bXjr3vbhBbynZ8SwqGE=</latexit>
<latexit sha1_base64="hnJ+4vLmYL7ONXRI/h4zSG5Blzo=">AAACJ3icbVBNT9tAFHyG0qYmlMCVywqExCmyubRHJC70FiqSIMUmWm+ek1XWa2v3GSmy/Jt66S+p1AMcihB/hHWSSuVjtCuNZnY1701SKGkpCO68jc0PWx8/tT772+2dL7udvfbA5qUR2Be5ys11wi0qqbFPkhReFwZ5ligcJvPzxh/eorEy11e0KDDO+FTLVApOThp3vkcKUxr5UYJTqStuDF/Ulaj9KPp3UE/Wuh8ZOZ1R7EdSRxmnWZJUP+qbSteM+ePOUdANlmBvSbgmR7BGb9z5HU1yUWaoSShu7SgMCopdFEmh0IWVFgsu5nyKI0c1z9DG1XLlmh07ZcLS3LiriS3V/39UPLN2kSXuZTOofe014nveqKT0W1xJXZSEWqyC0lIxylnTH5tIg4LUwhEujHSzMjHjhgtyLTclhK9XfksGp90w6IaXAbTgAA7hBEL4CmdwAT3og4Cf8Af+woP3y7v3Hld1bXjr3vbhBbynZ8SwqGE=</latexit>
<latexit sha1_base64="qzp6qQPmWnjk4ReJk9tuCOUBTOA=">AAACMnicbVBNS8NAEN34WeNX1aOXxSJ4KokXPQpe9KZiq9DEstlO2sXNJuxOhBLym7z4SwQPelDEqz/CTY3g17ALj/dmeDMvyqQw6HmPztT0zOzcfGPBXVxaXlltrq13TZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6sNIvbkAbkapzHGcQJmyoRCw4Q0v1m8eBhBh7bhDBUKiCac3GZcFLNwi+HqhBzbuBFsMRhm4gVJAwHEVRcVZeFaqk1O03W17bmxT9C/watEhdJ/3mfTBIeZ6AQi6ZMT3fyzC0Vii4BGuWG8gYv2ZD6FmoWAImLCYnl3TbMgMap9p+hXTCfp8oWGLMOIlsZ7Wo+a1V5H9aL8d4PyyEynIExT+N4lxSTGmVHx0IDRzl2ALGtbC7Uj5imnG0KVch+L9P/gu6u23fa/unXutgt46jQTbJFtkhPtkjB+SInJAO4eSWPJBn8uLcOU/Oq/P22Trl1DMb5Ec57x8FLqnq</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
<latexit sha1_base64="H2ojkUv6xoIXh/dZUhqXHtKfwhI=">AAACMnicbVBNS8QwEE39tn6tevQSXARPSyuCHhe86E3FVWFblzQ73Q2maUmmwlL6m7z4SwQPelDEqz/CdK3g15DA470Z3syLMikMet6jMzE5NT0zOzfvLiwuLa80VtfOTZprDh2eylRfRsyAFAo6KFDCZaaBJZGEi+j6oNIvbkAbkaozHGUQJmygRCw4Q0v1GkeBhBi7bhDBQKiCac1GZcFLNwi+Hqh+zbuBFoMhhm4gVJAwHEZRcVpeFaqk1O01ml7LGxf9C/waNEldx73GfdBPeZ6AQi6ZMV3fyzC0Vii4BGuWG8gYv2YD6FqoWAImLMYnl3TLMn0ap9p+hXTMfp8oWGLMKIlsZ7Wo+a1V5H9aN8d4PyyEynIExT+N4lxSTGmVH+0LDRzlyALGtbC7Uj5kmnG0KVch+L9P/gvOd1q+1/JPdpvtnTqOObJBNsk28ckeaZNDckw6hJNb8kCeyYtz5zw5r87bZ+uEU8+skx/lvH8ABm6p7g==</latexit>
A =
2
6
6
4
0110
1010
1101
0010
3
7
7
5
2 R
n⇥n
<latexit sha1_base64="IY45M3e7jKl2yOFMl66x3TQQ12Y=">AAADBHiclVLNTtwwEHbSH2hoy1Ju7cWwatXTKkFI9FKJqheOtGIBaR1WjjPZtXCcYE8qraI99NJX6YUDCHHlIXrr2+DsplILtCoj2fN5Zj7NjycplbQYhj89/8HDR48XFp8ES0+fPV/urLzYt0VlBPRFoQpzmHALSmroo0QFh6UBnicKDpLjj43/4AsYKwu9h5MS4pyPtMyk4OhMwxXv5Yf3lJ1UPKUBU5DhwOkERlLX3Bg+mdbCyTRga2wtbC76hjYq+guexzBGg7s992H8m/2LEf53joCBTtu23MPI0RhjJjXLOY6TpP48Pao1Q5mDpdpFDDvdsBfOhN4GUQu6pJXdYecHSwtR5aBRKG7tIApLjF1GlEKBG2JloeTimI9g4KDmLlNczz5xSl87S0qzwrijkc6svzNqnls7yRMX2dRrb/oa412+QYXZu7iWuqwQtJgnyipFsaDNRtBUGhCoJg5wYaSrlYoxN1yg25tmCNHNlm+D/Y1eFPaiT5vd7Y12HIvkFVknb0lEtsg22SG7pE+E99X77p155/43/9S/8C/nob7XclbJH+JfXQOl2NdA</latexit>
<latexit sha1_base64="IY45M3e7jKl2yOFMl66x3TQQ12Y=">AAADBHiclVLNTtwwEHbSH2hoy1Ju7cWwatXTKkFI9FKJqheOtGIBaR1WjjPZtXCcYE8qraI99NJX6YUDCHHlIXrr2+DsplILtCoj2fN5Zj7NjycplbQYhj89/8HDR48XFp8ES0+fPV/urLzYt0VlBPRFoQpzmHALSmroo0QFh6UBnicKDpLjj43/4AsYKwu9h5MS4pyPtMyk4OhMwxXv5Yf3lJ1UPKUBU5DhwOkERlLX3Bg+mdbCyTRga2wtbC76hjYq+guexzBGg7s992H8m/2LEf53joCBTtu23MPI0RhjJjXLOY6TpP48Pao1Q5mDpdpFDDvdsBfOhN4GUQu6pJXdYecHSwtR5aBRKG7tIApLjF1GlEKBG2JloeTimI9g4KDmLlNczz5xSl87S0qzwrijkc6svzNqnls7yRMX2dRrb/oa412+QYXZu7iWuqwQtJgnyipFsaDNRtBUGhCoJg5wYaSrlYoxN1yg25tmCNHNlm+D/Y1eFPaiT5vd7Y12HIvkFVknb0lEtsg22SG7pE+E99X77p155/43/9S/8C/nob7XclbJH+JfXQOl2NdA</latexit>
<latexit sha1_base64="IY45M3e7jKl2yOFMl66x3TQQ12Y=">AAADBHiclVLNTtwwEHbSH2hoy1Ju7cWwatXTKkFI9FKJqheOtGIBaR1WjjPZtXCcYE8qraI99NJX6YUDCHHlIXrr2+DsplILtCoj2fN5Zj7NjycplbQYhj89/8HDR48XFp8ES0+fPV/urLzYt0VlBPRFoQpzmHALSmroo0QFh6UBnicKDpLjj43/4AsYKwu9h5MS4pyPtMyk4OhMwxXv5Yf3lJ1UPKUBU5DhwOkERlLX3Bg+mdbCyTRga2wtbC76hjYq+guexzBGg7s992H8m/2LEf53joCBTtu23MPI0RhjJjXLOY6TpP48Pao1Q5mDpdpFDDvdsBfOhN4GUQu6pJXdYecHSwtR5aBRKG7tIApLjF1GlEKBG2JloeTimI9g4KDmLlNczz5xSl87S0qzwrijkc6svzNqnls7yRMX2dRrb/oa412+QYXZu7iWuqwQtJgnyipFsaDNRtBUGhCoJg5wYaSrlYoxN1yg25tmCNHNlm+D/Y1eFPaiT5vd7Y12HIvkFVknb0lEtsg22SG7pE+E99X77p155/43/9S/8C/nob7XclbJH+JfXQOl2NdA</latexit>
<latexit sha1_base64="IY45M3e7jKl2yOFMl66x3TQQ12Y=">AAADBHiclVLNTtwwEHbSH2hoy1Ju7cWwatXTKkFI9FKJqheOtGIBaR1WjjPZtXCcYE8qraI99NJX6YUDCHHlIXrr2+DsplILtCoj2fN5Zj7NjycplbQYhj89/8HDR48XFp8ES0+fPV/urLzYt0VlBPRFoQpzmHALSmroo0QFh6UBnicKDpLjj43/4AsYKwu9h5MS4pyPtMyk4OhMwxXv5Yf3lJ1UPKUBU5DhwOkERlLX3Bg+mdbCyTRga2wtbC76hjYq+guexzBGg7s992H8m/2LEf53joCBTtu23MPI0RhjJjXLOY6TpP48Pao1Q5mDpdpFDDvdsBfOhN4GUQu6pJXdYecHSwtR5aBRKG7tIApLjF1GlEKBG2JloeTimI9g4KDmLlNczz5xSl87S0qzwrijkc6svzNqnls7yRMX2dRrb/oa412+QYXZu7iWuqwQtJgnyipFsaDNRtBUGhCoJg5wYaSrlYoxN1yg25tmCNHNlm+D/Y1eFPaiT5vd7Y12HIvkFVknb0lEtsg22SG7pE+E99X77p155/43/9S/8C/nob7XclbJH+JfXQOl2NdA</latexit>