理解ARIMA时间序列预测模型

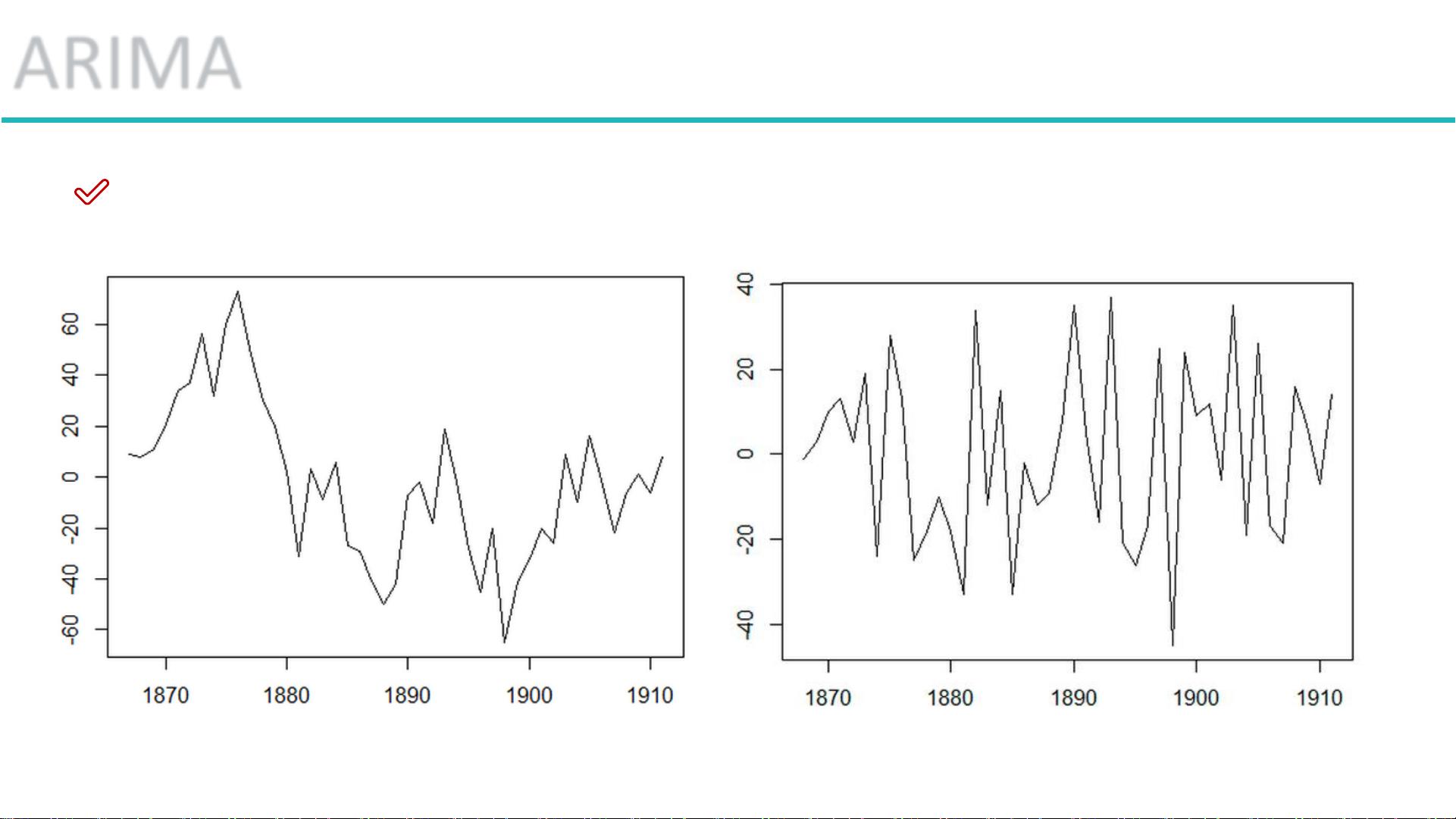
"ARIMA时间序列预测模型是经典的数据分析工具，主要用于处理具有趋势和季节性的序列。本文将深入探讨ARIMA模型的理论基础，包括平稳性、差分、自回归（AR）、移动平均（MA）和自回归移动平均（ARMA）模型，以及自相关函数（ACF）和偏自相关函数（PACF）的应用。" ARIMA模型是统计学和时间序列分析中的一个重要概念，全称是差分自回归移动平均模型，用于预测具有自相关性的时间序列数据。模型由三个参数组成：p代表自回归项的数量，d代表差分次数，q则表示移动平均项的数量。ARIMA模型的核心是将非平稳序列通过差分转换为平稳序列，然后用自回归和移动平均的方法来建模。 平稳性是ARIMA模型的基础，意味着序列的均值和方差保持恒定，且序列的统计特性不会随时间改变。为了实现这一目标，有时需要对原始数据进行差分处理，即计算时间序列在相邻时刻的差值，以消除趋势或季节性。一阶差分是最常见的，但可能需要多次差分以达到平稳。 自回归模型（AR）描述了当前值与过去值之间的关系，它假设当前的观测值可以由其历史值线性组合来预测。AR模型要求数据平稳，且自相关系数显著。自回归模型的阶数p决定了模型考虑的过去值的数量。 移动平均模型（MA）关注的是自回归模型中误差项的累加，它通过过去误差项的影响来预测当前值。移动平均模型有助于减少随机波动，并要求误差项具有一定的自相关性。 自回归移动平均模型（ARMA）是AR和MA的结合，能同时捕捉自回归和移动平均效应。ARMA(p,q)模型中，p是自回归项的个数，q是移动平均项的个数。 自相关函数（ACF）和偏自相关函数（PACF）是识别ARIMA模型阶数的重要工具。ACF衡量序列在不同滞后下的自相关程度，而PACF则揭示了序列中直接的因果关系，对于识别自回归模型的阶数p特别有用。当PACF在某点后快速衰减至零时，这通常指示了一个AR(p)模型的阶数。 在实际应用中，ARIMA模型广泛应用于经济、金融、气象、社会科学等领域的时间序列预测，例如股票价格预测、销售量预测等。Facebook的Prophet库也是基于类似的原理，但提供了更高级的接口和对季节性、趋势的处理能力。 ARIMA模型通过结合自回归、差分和移动平均方法，提供了一种强大而灵活的工具来分析和预测非平稳时间序列数据。理解这些基本概念是有效运用ARIMA模型的关键，而正确选择模型参数p、d、q则需要对数据的平稳性、自相关性和季节性有深刻理解。