使用离散状态转移算法解决旅行商问题的Python实现

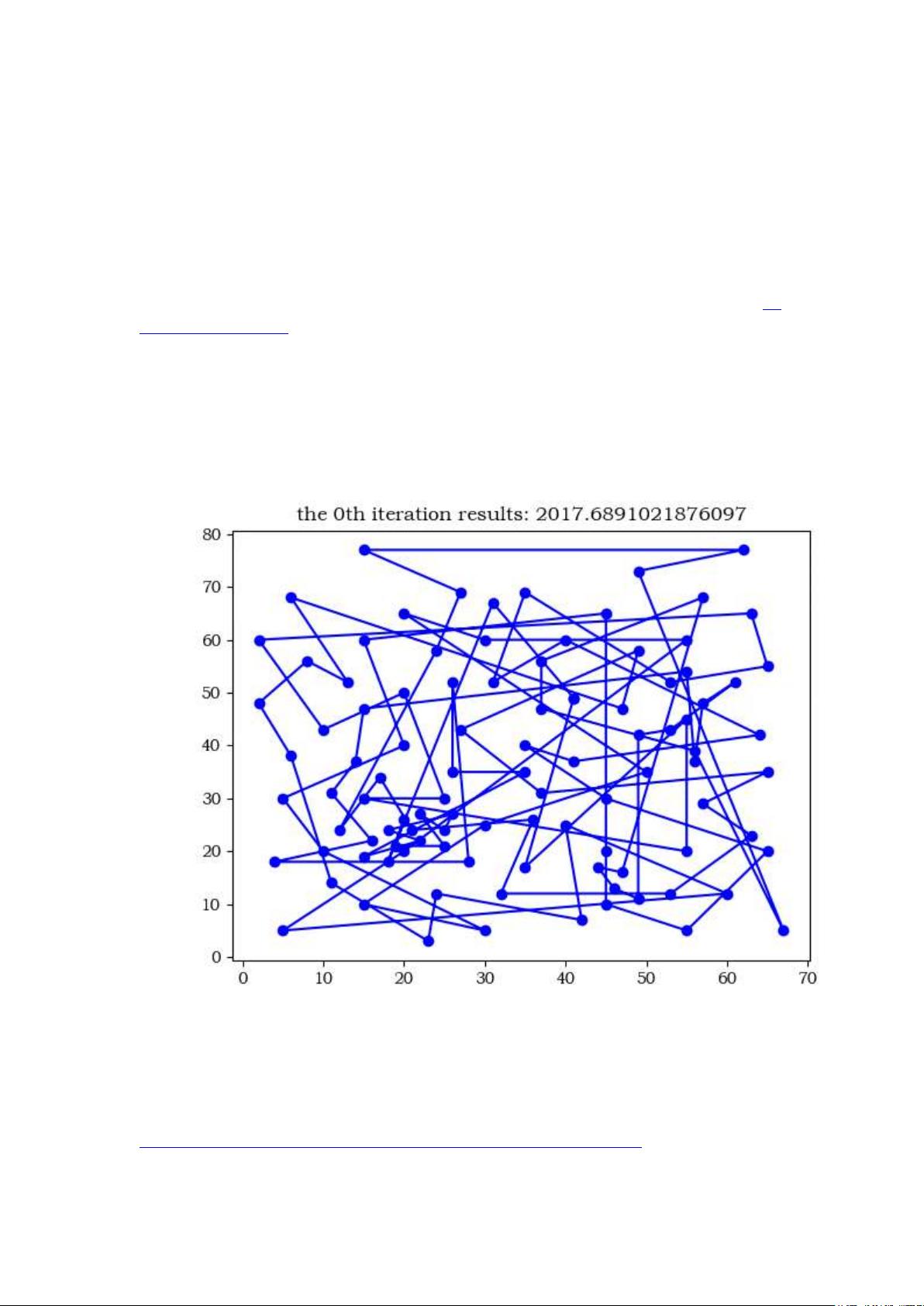
"离散状态转移算法(DSTA)是一种用于解决旅行商问题(TSP)的优化方法。旅行商问题是一个经典的组合优化问题，目标是找到访问所有城市一次并返回起点的最短路径，且每个城市只能访问一次。该问题被证明为NP-hard，意味着在多项式时间内找到最优解是困难的。 在给定的Python程序中，作者提供了一个DSTA的实现。程序主要包含两个关键部分：交换算子和对称算子，它们用于生成候选解来探索解决方案空间。 1. **初始化**: 在`DSTA`类的初始化函数中，`fun`参数代表计算距离的函数，`Best`表示当前最佳解，`SE`是搜索空间大小，`MaxIter`是最大迭代次数。这些参数定义了算法的基本配置。 2. **交换算子** (`op_swap`): 这个函数通过随机选择两个城市并交换它们的位置来生成新的候选解。这种方法增加了路径多样性，有助于跳出局部最优。随机生成的排列`R`用于确定要交换的城市`a`和`b`，然后将它们在路径中的位置互换。 3. **对称算子** (`op_symmetry`): 对称算子更复杂，它通过反转路径中的一段来生成新的解。选取两个城市`a`和`b`，如果`a`小于`b`，则反转`a`到`b`之间的城市顺序；否则，反转`b`到`a`的顺序。这种操作可以产生与原路径对称的新路径，增加解的空间多样性。 4. **GitHub链接**: 提供的GitHub链接指向了一个名为`DSTA_TSP_python_version`的项目，其中包含了`DSTA.py`文件，这是实现DSTA算法的Python脚本。用户可以通过下载该项目来查看完整代码并运行算法。 5. **文件结构**: `DSTA.py`文件是算法的核心，可能还包含了其他辅助函数和数据处理部分，用于读取城市距离矩阵，计算路径长度，更新最佳解等。 6. **算法流程**: 算法通常会进行多次迭代，每次迭代中使用交换算子和对称算子生成多个候选解，评估这些解的适应度（即路径长度），并根据设定的策略更新当前最佳解。这个过程会持续到达到最大迭代次数或满足其他停止条件。 通过这样的离散状态转移算法，虽然无法保证找到全局最优解，但可以在合理的时间内找到接近最优的解决方案，对于解决实际规模较小的旅行商问题具有一定的实用价值。