理解递归算法：从数据结构与实例解析

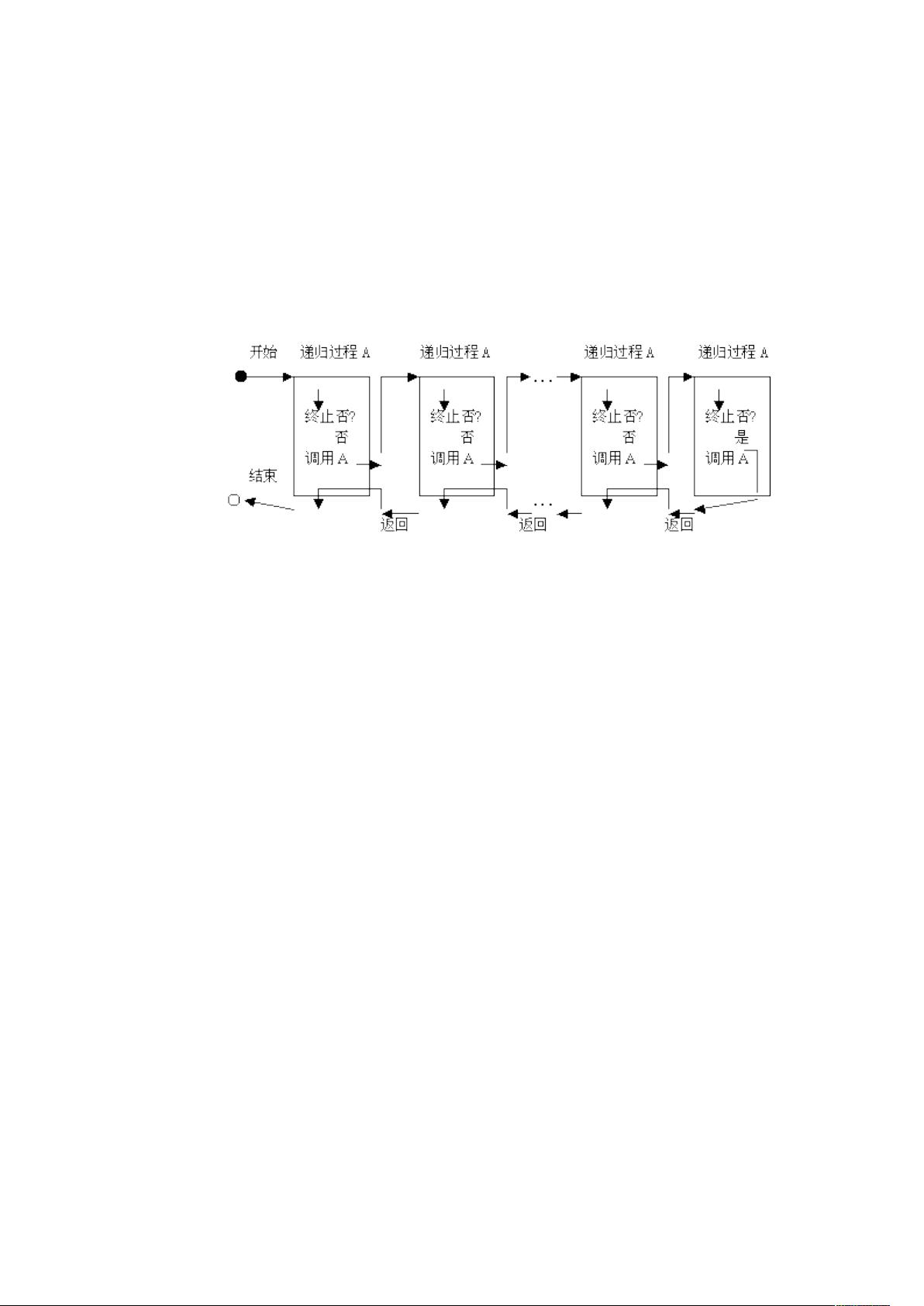
"趣谈数据结构（五）深入解析递归算法，适合信息学奥赛学习者及编程爱好者。” 在趣谈数据结构系列的第五部分，我们聚焦于递归算法这一重要概念。递归算法是程序设计中的核心技巧，尽管它可能是初学者难以掌握的。递归的基本原理在于一个函数或过程能通过调用自身来解决问题，形成一种自我嵌套的执行模式。这种模式在执行过程中，不断地深入并返回，直到满足某个终止条件，然后逐层返回，最终得出结果。 递归算法的执行流程如图1所示，形象地描绘了这个过程。每次递归调用都会将当前状态传递给下一次调用，直到遇到基本情况（通常是最简单的无法再分解的情况），然后逐级返回并处理结果，最终完成整个计算。 递归的优势在于它可以简化复杂的、有规律的问题解决过程。比如，我们可以用递归来计算阶乘。阶乘的定义是1到N的所有整数的乘积，可以用递归方式表示为N*(N-1)!。递归调用的过程是从N递减到1，每次调用都将N减1并乘以前面的阶乘结果。以下是一个用Pascal编写的递归阶乘计算示例： ```pascal program Ex11_10; var n: byte; t: extended; procedure find(n: byte); begin if n = 1 then t := 1 else begin find(n - 1); t := t * n; end; end; begin write('N='); readln(n); find(n); writeln('N!=', t:1:0); end. ``` 在这个例子中，`find`过程会根据输入的N进行递归调用，直到N等于1，然后逐层返回并累积乘积，得出N的阶乘。 另一个应用递归的例子是计算菲波纳契数列的第N项。菲波纳契数列的定义是：F(1)=1, F(2)=1, F(n)=F(n-1)+F(n-2) (n>=3)。递归实现如下： ```pascal function Fibonacci(n: integer): integer; begin if n <= 2 then Fibonacci := 1 else Fibonacci := Fibonacci(n - 1) + Fibonacci(n - 2); end; ``` 这里，`Fibonacci`函数根据给定的n值，如果n小于或等于2，则返回1，否则递归调用自身计算前两项之和。 然而，需要注意的是，虽然递归能够写出简洁的代码，但它的效率并不总是最高的。因为每次递归调用都会产生额外的系统开销，如栈空间的使用。对于大规模的数据或深度递归，可能会导致栈溢出等问题。因此，在实际编程中，有时会考虑使用循环或者其他非递归方法来优化性能。 递归算法在解决特定问题时展现出优雅的代码结构和强大的解决问题的能力。在信息学奥赛和编程竞赛中，掌握递归的使用是必不可少的技能，因为它可以帮助解决许多有规律的复杂问题，如树的遍历、动态规划等。然而，使用递归时也需要权衡其效率，适时选择更适合的算法策略。