频域图像增强技术及其应用

"图像处理 频域增强" 在图像处理领域，频域增强是一种重要的技术，它通过在图像的频率域内操作来改善图像的质量和视觉效果。本课件详细介绍了频域增强的原理和各种滤波器，适用于通信工程学院信息工程专业的学生学习。 频域增强的基本思想是直接在图像的傅立叶变换系数上进行操作，这些系数代表了图像的频率成分。二维离散傅立叶变换（DFT）是将图像从空域转换到频域的关键工具。对于一个大小为M×N的图像f(x, y)，其傅立叶变换F(u, v)可以通过以下公式计算： \[ F(u, v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j2\pi(\frac{ux}{M} + \frac{vy}{N})} \] 傅立叶逆变换则用于将频率域中的处理结果转换回空域图像： \[ f(x, y) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) e^{j2\pi(\frac{ux}{M} + \frac{vy}{N})} \] 在频域中，不同位置的频率分量对应图像的不同特性。频率为0的分量（即原点，u=v=0）表示图像的平均灰度。远离原点的低频部分与图像的缓慢变化区域相关，如背景和平滑区域。而高频部分则对应图像的快速变化特征，如边缘、细节和噪声。 频域增强就是通过修改傅立叶变换系数来实现的。常见的滤波器类型包括： 1. 陷波滤波器：这种滤波器设计用于消除特定频率范围内的成分，例如可以用来去除特定噪声频段。 2. 低通滤波器：保留低频成分，减弱或消除高频成分，常用于平滑图像，去除噪声，但可能导致细节丢失。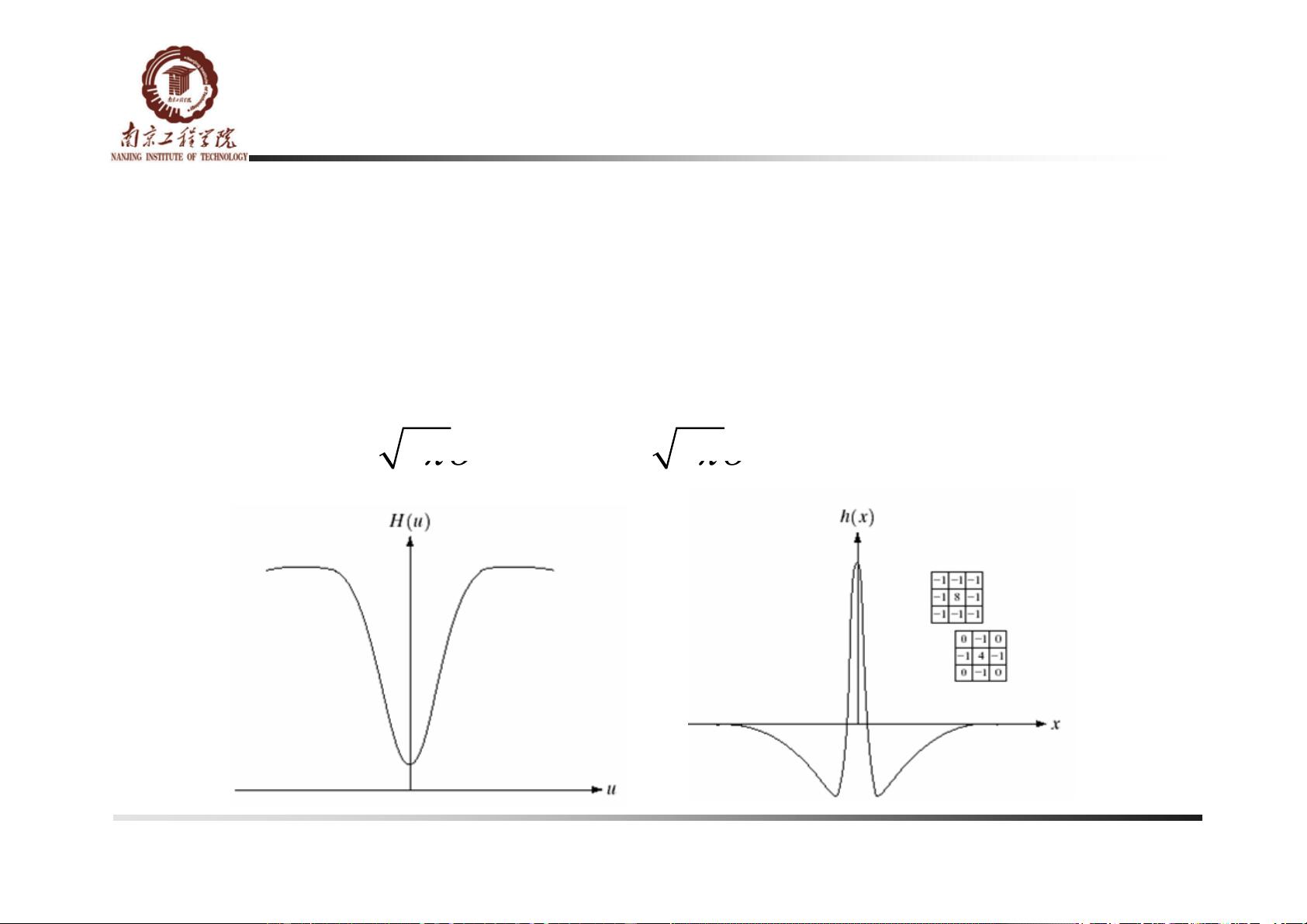 3. 高通滤波器：增强高频成分，使图像边缘更明显，常用于图像锐化，但过度使用可能导致噪声增强。 4. 同态滤波器：结合了低通和高通滤波，对图像的亮部和暗部应用不同的滤波策略，特别适用于处理反差低或光照不均的图像。 频域增强与空域滤波的关系可以理解为空域滤波是通过对图像进行卷积操作来实现的，这实质上是频域中滤波器与图像傅立叶变换的乘积，然后再进行逆傅立叶变换回到空域。 频域增强是图像处理中的核心概念，它利用傅立叶变换和各种滤波器来优化图像的视觉效果，适用于多种应用场景，如图像去噪、增强边缘、提高对比度等。理解和掌握这些原理对于进行复杂的图像处理任务至关重要。