统计分析指标与检验详解：从均值到F检验

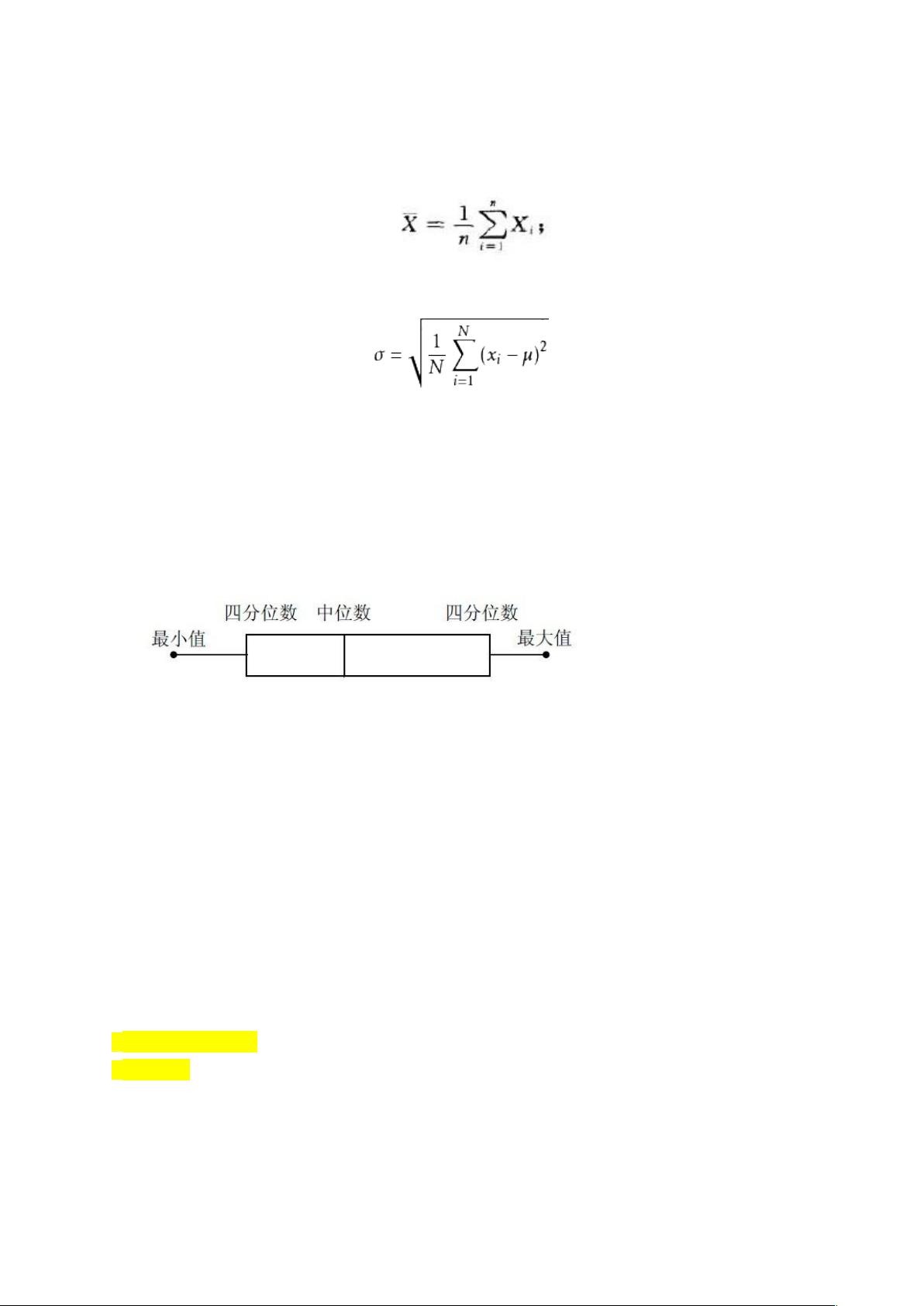
在IT领域，进行数据统计分析是至关重要的，它有助于我们理解并解释数据的性质和模式。本文将深入探讨常用的统计分析指标和检验方法，以支持决策制定和数据分析。 首先，**常用统计量**是评估数据集中趋势和离散程度的基础。**均值**（mean）代表数据集的中心位置，而**标准差**（Standard Deviation，SD）或**标准偏差**，反映了数据的分散程度。对于总体标准差，计算公式涉及除以n（STDEVP），而在样本中，通常除以(n-1)（STDEV），后者提供了无偏估计。**变异系数**（Coefficient of Variation, CV）则是标准差与均值的比例，用于衡量数据离散程度的相对大小，当CV大于15%时，可能表明数据分布异常。 箱线图（Box-plot）和图基5数（Turkey’s Five Number）通过最小值、第一四分位数Q1、中位数、第三四分位数Q3和最大值，以及四分位数间距IQR来可视化数据分布的离散情况。异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的数值，这些值在分析中可能需要剔除。 **异常值判断**不仅依赖于CV，还根据数据分布情况考虑，如正态分布下，超过均值2个或3个标准差被认为是异常。此外，**峰度**和**偏度**是对数据形状的描述，它们分别衡量数据分布的尖锐程度和对称性。 在统计检验方面，**Z检验**用于已知标准差时，验证一组数据的均值与特定值是否相符，分为双边和单边检验。**T检验**，特别是**Student's t-test**，适用于小样本或总体方差未知的情况，分为单样本、双边、单边和双样本（方差齐性检验），有时需先做方差分析（ANOVA）。 **F检验**，又称**方差齐性检验**，在比较两个或多个样本的均值时，检查各组方差是否一致。当方差不等时，可能需要进行**t'检验**或变量变换。 最后，**方差分析**（ANOVA）用于多组数据的比较，最常见的是**单因素方差分析**，考察单一因素对一个或多个响应变量的影响。 掌握这些统计分析指标和检验方法，可以帮助IT专业人士有效地处理和解释大量数据，确保结果的准确性和可靠性，从而在项目管理、数据挖掘和机器学习等领域做出明智的决策。