KMP算法深入解析：提升字符串匹配效率

"KMP字符串模式匹配是一种在主串中高效定位目标子串的算法，相较于简单的暴力匹配，其时间复杂度更低，为O(m+n)。KMP算法避免了不必要的回溯，通过预处理得到部分匹配表，使得在发生不匹配时可以直接跳过已匹配的部分，提高效率。" KMP算法，全称Knuth-Morris-Pratt算法，是由D.E.Knuth、V.R.Morris和J.H.Pratt三位学者于1970年提出的一种字符串匹配算法。该算法的主要目标是在一个大文本串（主串S）中查找一个较小的目标串（模式串T），并找到所有匹配的位置。 **一、简单匹配算法** 简单匹配算法是最直观的字符串匹配方法，也称为暴力匹配。其基本思路是：从主串S的任意位置开始，逐字符与模式串T进行比较。如果在某处比较不匹配，就将模式串移到主串的下一个位置，然后重新从头开始比较。这种方法的效率较低，因为每次失配都需要将模式串回溯到起始位置，时间复杂度为O(m*n)，其中m为模式串长度，n为主串长度。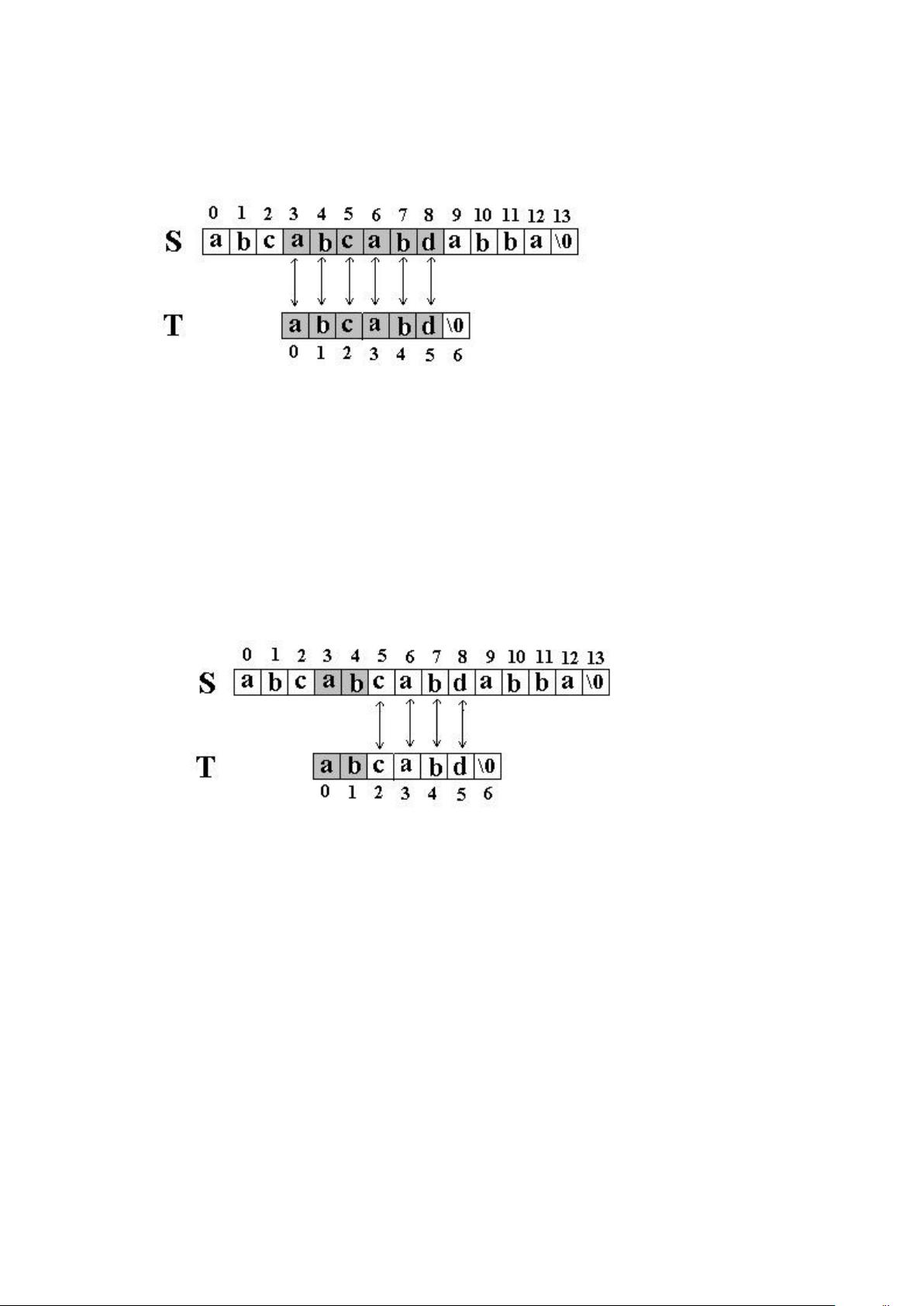 **二、KMP算法的核心思想** KMP算法的关键在于通过构造部分匹配表（也叫失配表）来优化匹配过程。部分匹配表记录了在模式串中遇到不匹配时，模式串已经匹配了多少字符，从而可以避免不必要的回溯。例如，如果在模式串T的第i个位置发生失配，根据部分匹配表，我们可以直接将模式串的指针移动到第part[i]个位置，而不是回到开头。 部分匹配表的构建基于模式串的前后缀关系。如果模式串的前缀和后缀有相同的情况，那么在发生失配时，我们可以利用这些相同的部分，不必完全回溯。 **三、KMP算法步骤** 1. 构建部分匹配表（Prefix Function）：对于模式串T，计算出每个位置i对应的最长前后缀相同长度值part[i]。例如，模式串"abca"的part数组为{0, 0, 1, 0}，表示在"abca"的末尾，"a"与前面的"aca"有相同的前缀，长度为1。 2. 初始化两个指针i和j，分别指向主串S和模式串T的起始位置。 3. 比较S[i]和T[j]，如果相等，i和j都加1；如果不等，根据part[j]的值，将模式串的指针j回溯到part[j]位置，主串的指针i保持不变。 4. 重复步骤3，直到模式串遍历完或者找到匹配的子串。 **四、KMP算法的优势** KMP算法避免了在简单匹配算法中频繁的回溯操作，提高了匹配效率。即使在最坏情况下，KMP算法的时间复杂度也能保证在O(m+n)，这是因为它能有效利用已知的匹配信息，减少了无效的比较次数。 总结，KMP字符串模式匹配算法是解决字符串匹配问题的一个高效解决方案，通过预处理得到的部分匹配表，实现了在主串中快速定位模式串的功能，显著提升了算法的效率。