使用并查集模拟渗透问题的蒙特卡洛实验

"实验一：渗透问题（Percolation）1" 在本次实验中，我们主要探讨了渗透问题，这是基于合并-查找（union-find）数据结构的一种应用，使用Java编程语言进行实现。实验的主要目标是通过蒙特卡洛模拟估计渗透阈值。实验环境为IntelliJ IDEA 2018.2.5 Ultimate Edition，在Windows 10操作系统上运行，使用JRE 1.8.0_152和OpenJDK 64-Bit Server VM。 实验的第一部分是构建`Percolation`类。在这个类中，我们定义了一个n*n的网格，其中每个点可以是Open（开放）或Closed（关闭）状态。当最底部的点与最顶端的点连通时，我们就认为这个网格系统是渗透的。并查集在这里起到了关键作用，因为它能够高效地判断不同点之间是否连通。在实现中，我们添加了两个虚拟节点，分别与顶部和底部节点连接，每次打开一个点，就会将其与相邻的开放点合并到同一集合。如果顶部和底部的虚拟节点位于同一集合，那么系统就被认为是渗透的。 `Percolation`类的具体实现包括以下方法： 1. `public Percolation(int n)`: 初始化一个n*n的网格，所有点默认都是Blocked（封闭）状态。 2. `public void open(int row, int col)`: 打开指定位置（row, col）的点，如果该点尚未打开。 实验的第二部分是利用蒙特卡洛模拟来估算渗透阈值。这个过程包括： 1. 创建一个全为Blocked的n*n网格系统。 2. 随机选择一个点并将其设为Open，然后不断重复此过程，直到整个系统变为渗透状态。 3. 重复上述过程T次，收集数据，计算平均值、标准差以及96%置信区间。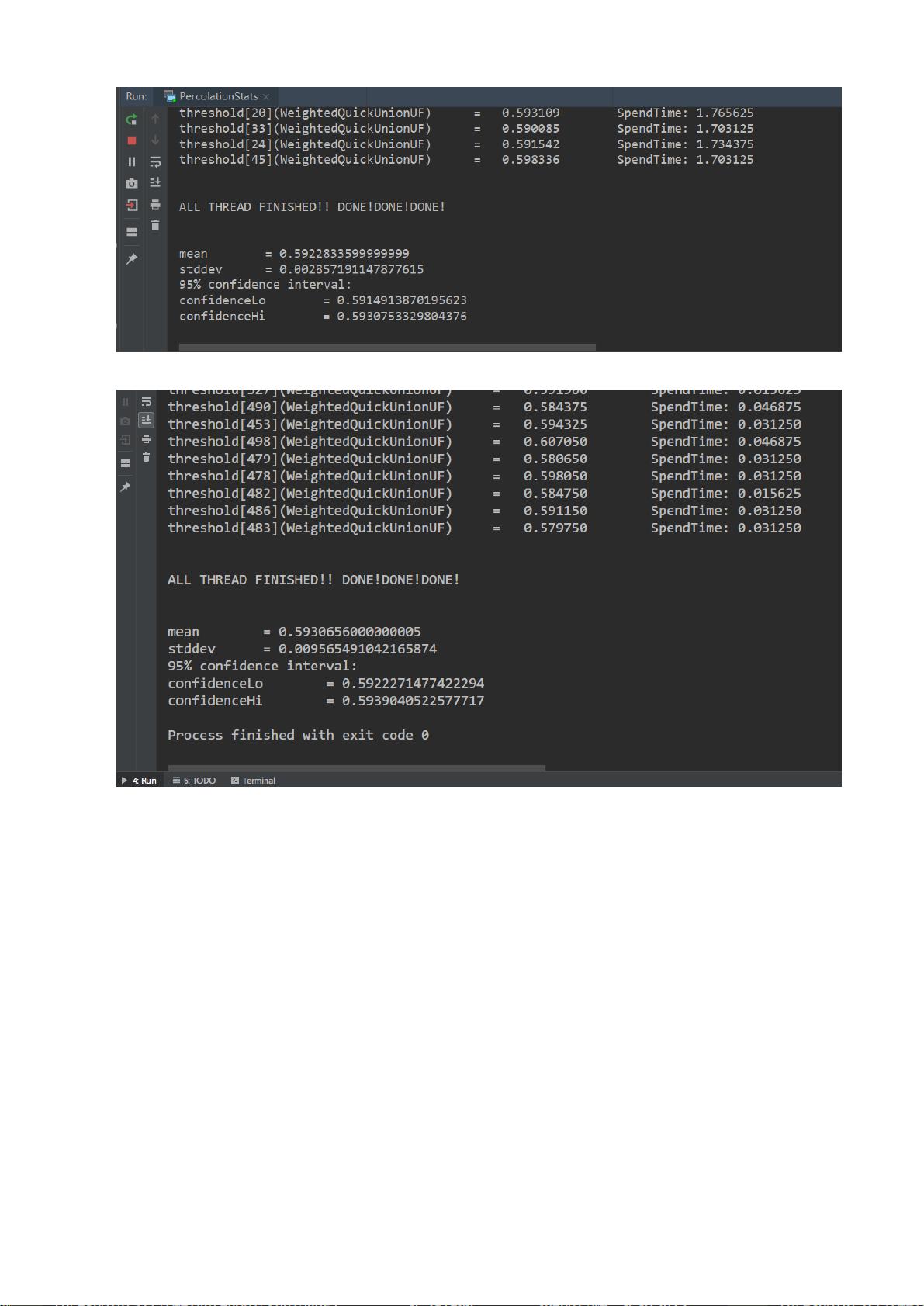 4. 使用WeightedQuickUnion并查集优化大规模网格的处理，并进行多次渗透测试，以找到95%置信区间的渗透阈值。 5. 分别对2000和1000大小的网格进行50次模拟，观察并记录结果。 实验中还引入了多线程技术，以提高计算效率，尤其是在处理大规模网格时。通过这种方式，我们可以更有效地进行大量渗透测试，从而得出更精确的渗透阈值估计。 本实验结合了数据结构（并查集）、随机算法（蒙特卡洛模拟）以及并行计算等概念，以解决实际问题——渗透问题。实验的结果有助于理解这些理论知识在实践中的应用，同时展示了如何通过编程技术来优化复杂问题的求解。