离散时间系统分析：线性时不变系统与差分方程

"该资源是《信号与系统》第四版的第8章，主题是离散时间系统的时域与变换域分析，主要内容包括离散时间系统的基本概念、差分方程的求解、线性时不变系统、数字滤波器的原理与结构、离散系统的频响特性、单位样值响应和系统函数的分析，以及如何运用MATLAB进行离散时间系统的分析。" 在离散时间系统的研究中，系统通常被描述为一个对输入信号进行转换的装置，输出信号由输入信号经过特定运算得到。离散时间系统的一个显著优点是其在计算机处理中的高精度、良好的可靠性、功能灵活性以及便于实现时分复用和保密通信。此外，由于集成电路技术的发展，离散时间系统易于实现大规模集成。 8.1章节介绍了离散时间系统与差分方程，其中线性时不变（LTI）系统是一个重要的概念。线性系统满足叠加性和均匀性，即输入信号的加权和通过系统后，输出也是这些加权和的对应输出。而时不变性意味着如果输入信号延迟，那么输出也将相应延迟，而不改变其形状。例如，例8.1-1通过对比不同情况下的输出，展示了非线性和非时不变性的例子。 8.1.1节进一步讨论了线性时不变离散时间系统，指出如果一个系统对于输入信号x[n]的响应为y[n]，那么对于输入信号x[n-m]，响应应该是y[n-m]，这就是时不变性的定义。在例8.1-2中，分析了滑动平均滤波器的线性特性和时不变性，显示了该系统符合线性但不具备严格的时不变性。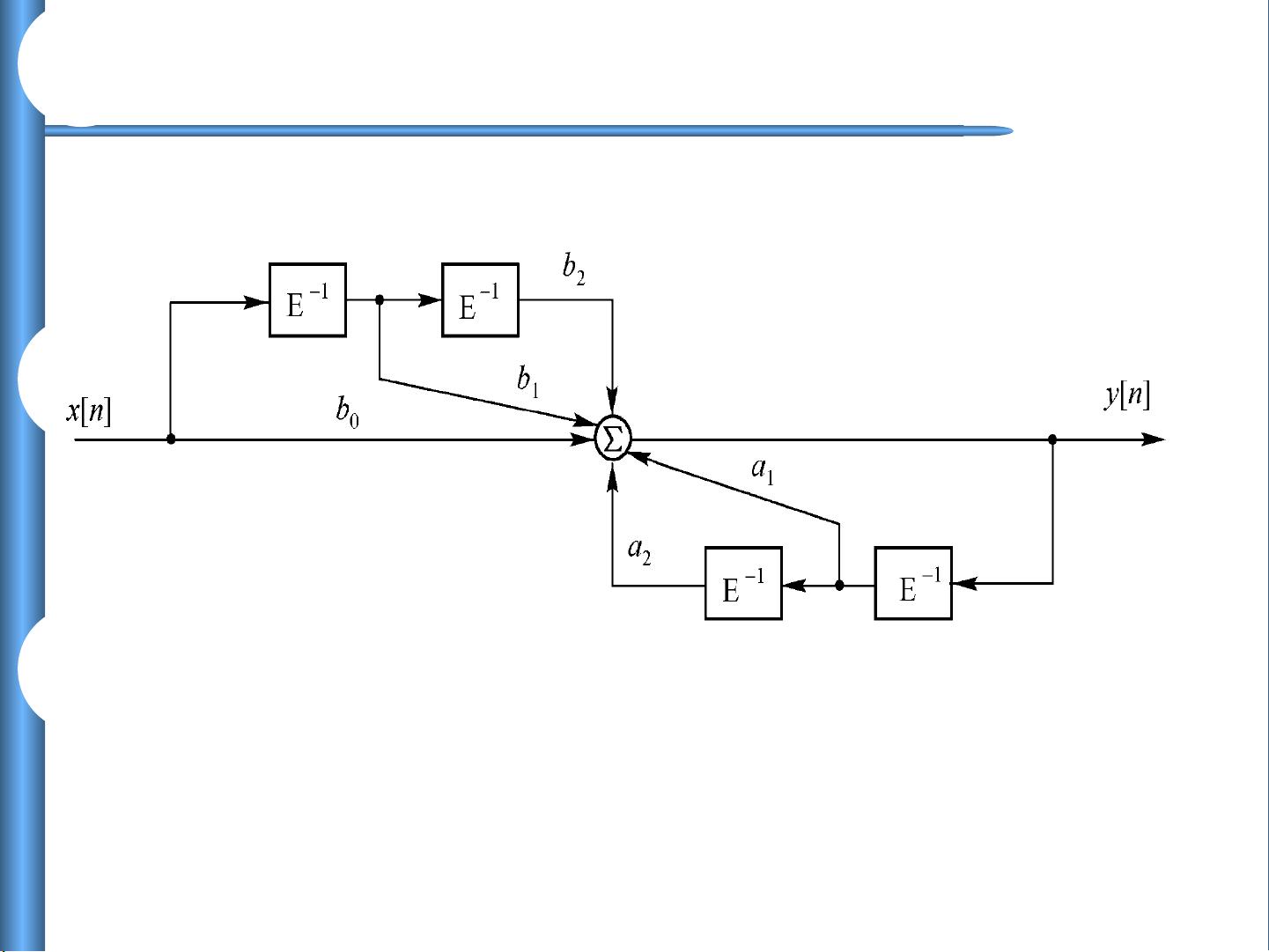 接下来的章节，8.2节涉及常系数线性差分方程的求解，这是描述离散时间系统行为的关键工具。8.3节讨论了离散系统的频响特性，这对于理解和设计数字滤波器至关重要。8.4节则深入到数字滤波器的原理和结构，这些滤波器在信号处理中有广泛应用，如噪声消除和信号整形。 8.5节介绍数字滤波器的设计，这部分通常涉及理论与实践结合，使用MATLAB等工具进行仿真和分析。最后，8.6节实际应用MATLAB来分析离散时间系统，这提供了直观的可视化和计算方法，有助于理解和验证理论分析。 这份资料涵盖了离散时间系统的基础理论和应用，对于学习信号处理、数字通信和相关领域的学生和工程师来说是非常宝贵的资源。