深入理解FFT：离散信号频谱分析与误差探讨

本文档主要介绍了如何利用快速傅里叶变换(FFT)对离散时间信号进行频谱分析。实验的主要目标包括深入理解离散傅立叶变换(DFT)的原理和FFT作为其快速算法的应用，以及掌握频谱分析过程中可能出现的误差及其原因。 实验的核心是理解FFT的工作原理，它将N个离散采样点通过计算转换为N个复数，每个复数对应一个特定频率的幅度和相位信息。在信号处理中，每个采样点n对应的频率范围是0到采样频率Fs，其中第一个点表示直流成分，最后一个点对应于Fs。FFT分析的频率分辨率由采样频率Fs和采样点数N决定，采样定理要求采样频率至少应是信号最高频率的两倍，以避免频率混叠。 实验内容包括对不同信号（如矩形序列x1(n), x2(n), x3(n)和余弦、正弦序列x4(n), x5(n)）进行频谱分析。对于信号x6(t)，提供了不同的采样频率fs和点数N，如16点、32点和64点，通过时域补零的FFT方法计算其频谱。分析过程中，会观察到随着点数增加，频谱分辨率提高，细节更加清晰，但同时可能会引入舍入误差，尤其是在较短的序列中。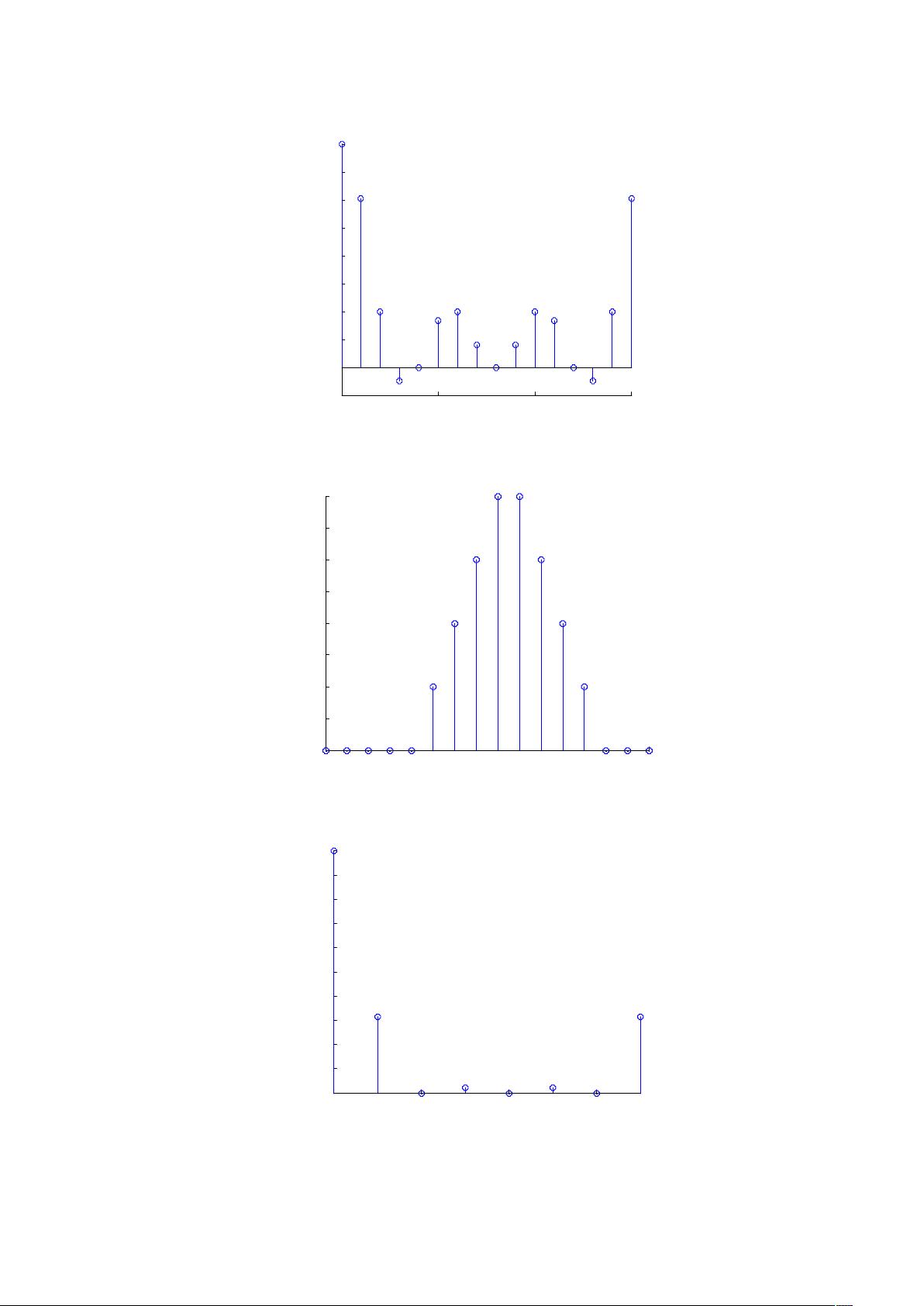 图1至图6展示了不同信号的频谱分布，如矩形序列在低频部分具有明显的峰值，而余弦和正弦序列则表现出典型的周期性特征。通过对这些图形的比较和分析，学生可以练习识别不同信号的特性，并理解如何根据实际需求选择合适的FFT点数来获取所需频率分辨率。 在实验结果与思考题部分，参与者需要理解和解释频谱图中的变化，例如频率响应的平坦度、峰-峰值和幅度衰减等。此外，还会涉及如何处理由于窗口函数或频谱泄漏带来的误差，以及如何通过优化采样率和FFT长度来减少误差。 总结来说，这个文档提供了一个实践性的学习平台，帮助读者掌握FFT在频谱分析中的应用，包括理解误差来源，选择合适的参数，以及如何正确解读和利用频谱信息。这对于IT专业人员在信号处理、通信系统设计或数据分析等领域都有着重要的实际价值。