WorldView-2多角度多时相遥感图像超分辨率重建操作方法

3星 · 超过75%的资源需积分: 50 158 浏览量更新于2024-07-28 收藏 9.79MB PDF 举报

本文主要探讨了多角度多时向遥感图像的超分辨率重建技术，针对WORLD-VIEW2卫星提出了一种创新的解决方案。研究者 Jianglin Ma、Jonathan Cheung-Wai Chan 和 Frank Canters在《IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing》上发表了这篇论文，旨在解决遥感图像中的高分辨率重建问题。首先，他们关注的是图像的精确配准（registration）阶段。为了处理局部几何变形和光谱差异带来的复杂性，作者提出了一个混合基于patch的注册方法。这种方法考虑到了诸如云层和云影等自然障碍物对图像匹配的影响，并在注册过程中对其进行有效的检测和处理，确保了后续处理的准确性。在图像重建（reconstruction）阶段，研究人员采用了L1范数数据拟合（L1 norm data fidelity）和Total Variation（TV）正则化相结合的模型。L1范数强调稀疏性，有助于去除噪声，而TV正则化则保持图像的边缘细节，使重构后的图像既保持高分辨率的特征，又保持整体的平滑性。他们通过最陡下降法（steepest descent method）有效地求解了这个重建目标函数，显示出该方法在处理大规模遥感数据上的高效性能。值得注意的是，该论文不仅提供了具体的技术细节，还展示了算法的实用性，因为它是设计为在实际操作环境中应用的，这意味着它能够处理实时或批量的多时相、多视角的WorldView-2遥感图像。这在遥感数据分析和地球观测领域具有重要意义，因为它能提升图像的解析能力，从而帮助科学家和决策者获取更精确的地理信息。总结来说，这篇文章贡献了一个完整的框架，包括图像配准的策略和超分辨率重建的优化模型，为提高多角度多时相遥感图像的质量提供了一种实用且高效的方法。这对于遥感图像处理领域的进一步发展和技术进步具有积极推动作用。

IEEE Proof

Web Version

6 IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING

where and are the -spatial, -spatial and

temporal derivative of

respectively. By substituting (11)

in (1 0) we get a quad ratic error function, which i s now linear

for its unknown

. Therefore, we obtain an analytic expression

for

(12)

where

and

.From(12)itseemsasifwe

can obtain the registration parameters

directly without itera-

tion. However, the estimator for

requires an estimator for ,

which also requires an estimator for

. Therefore, the expec-

tation-maximization ( EM) algorithm is used for s olvin g

,and

the whole algorithm procedure is deﬁned as follows:

1) Initialization: assign the ﬁxed constants

and , and pro-

vide initial estimate for

2) E-Step: compute

. This step also invo lves the pro cess of

classifying p ixels either into the

region or into the

region. Pixels belon gin g to have a close to zero weight.

3) M-Step: calculate

. This can be don e with the classical

differential method proposed in [7], which relies on a

Newton-Raphson style iterative scheme to approximate

the solution, and a Gaussian pyramid scheme to increase

the convergence speed.

4) The last two steps are repeated until the difference betw een

successive estimates of

falls below a small threshold

value.

3) Patch-Based Registration and Superresolution: In our ex -

periments the image patch size was set at 96

96 as a compro-

mise between accurate model adaptation and estimation. Once

image patches are accurately registered, it is important to elimi-

nate the blocking effect typical for patch-based approaches and

make sure that adjacent image patches match. There are two

ways to eliminate the blocking effect [23]: o ne is to apply an av-

eraging kernel with an appropriate size to smoo th the resulting

image, which will inevitably decrease the image qualit y; the

other is to div ide the image into overlapping blocks as show n

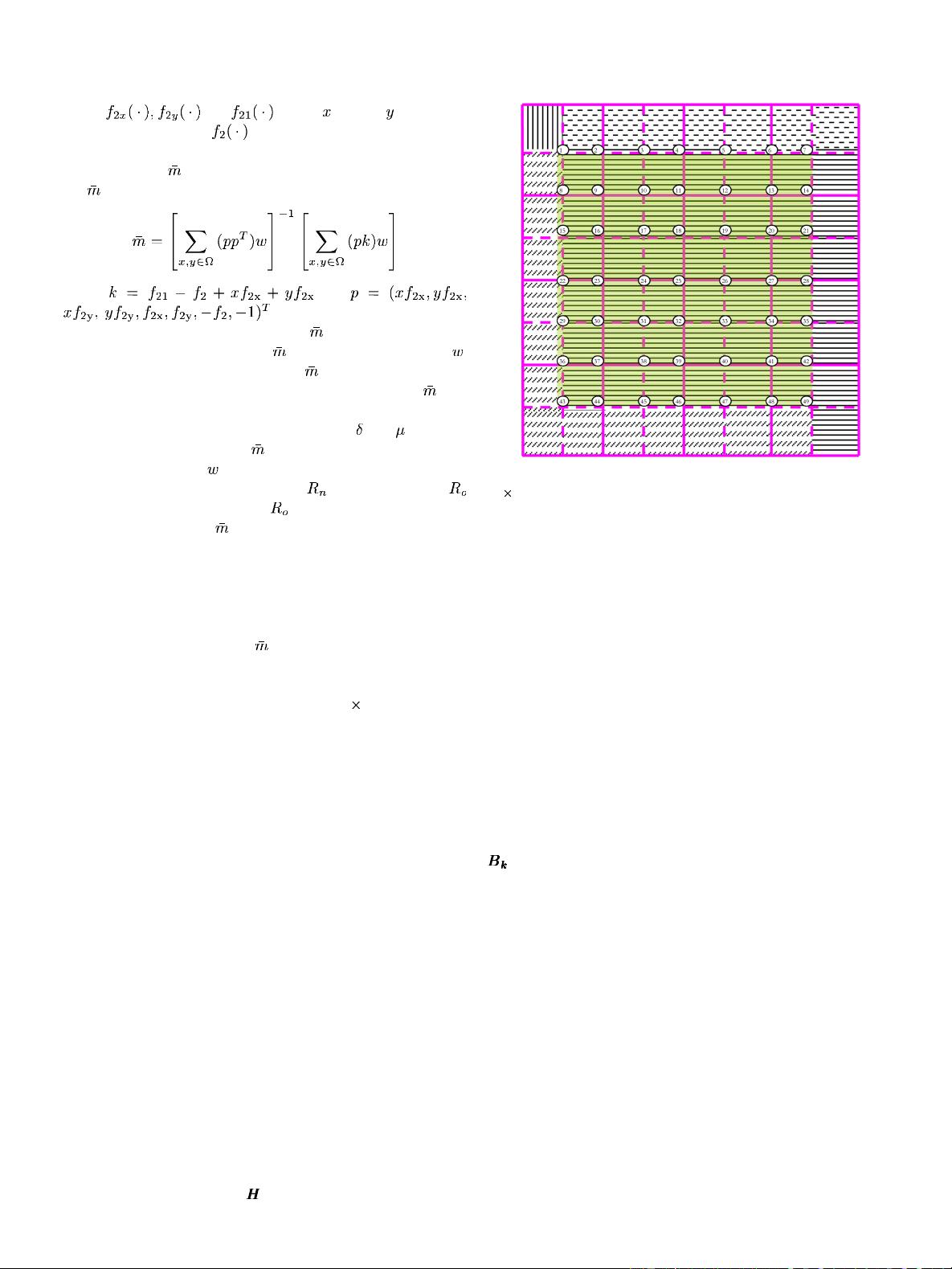
in Fig. 4, which is the method adopted in this pap er. In Fig. 4

the small tile is of size 48 by 48, and each image patch is com -

posed of four tiles. Using the moving window app ro ach, in t he

example there are 49 image patches all together instead of 16,

with the patch center indexed as i llustrated in Fig . 4. For any

image tile (except those near the edge) spatial consistency is

obtained by averaging the differences (geometric displacement,

photometric disparity and reconstructed discrepancy) for the

four ﬂoating patches the tile belongs to. By adopting this sliding

half-window m e th od, we can make sure that the transfo rmation

between images is locally afﬁne but globally smooth.

The patch-based scheme has the following m erits for SR:

1) Although the global transform is not invertible, for each

patch the transform is invertible, therefore state-of-the-art

SR algorithms can be implemented in this scheme.

2) Remote sensing images often have a large size; therefore

the construction of the

matrix in (2) may p ose compu-

tational problems. Constructing the matrix at patch level

Fig. 4. An illustration of overlappin g image patches. The small tile is of size

48, and the image patch is composed of 4 tiles. The solid line represents the

positions of non-overlappin g image patches while the dashed lines denote the

sliding positions. The centers of overlapping image patches are indexed from 1

and 49. Only the image tiles shown in green can be processed using the approach

proposed.

is efﬁcient and allows application of t he method on full-

size imagery. The patch-based scheme also enables par-

allel processing of SR.

3) Although patch-based image registration has been criti-

cized because image details may be overly smoothed, and a

polyafﬁne scheme has been proposed to solve this problem

[24], w e found that simple fusion of SR patches by aver-

aging d oes not deteriorate the SR result. In the spatially-

varying PSF image deconvoluti on literature, this simple fu-

sion method is comm on practice [20].

C. PSF E stimation and Construction of the H Matrix

From (2) we can see that the PSF that deﬁnes th e blur matrix

is applied on the und erlying HR image instead of on the LR

image. There are two ways to derive it, as follows:

1) One is referred to as the blind-SR metho d, which assu mes

that the HR image can be m odeled by means of an inho-

mogeneous image mod el such as the Potts-Markov model

[25]. However, the complexity of a remote sensing scene

often does not allow the use of this approach. Moreover,

the simultaneous estimation of t he PSF and the HR image

usually requires iteration and, therefore is computationally

heavy.

2) The other possibility is to ﬁrst estimate the PSF of the L R

image and th en linking it to the PSF of the underlying HR

image. Compared to estimating the PSF blindly, on-orbit

determination of the PSF of LR images, where the PSF

is calculated by w ay of speciﬁc objects in the observ ed

images, is more reliable. The local afﬁne assumption also

makes it easier to deﬁne the relationship b etween the PSF

of the LR i mage and that of the HR image. Therefore, in

this study this strategy is adopted .

剩余29页未读，继续阅读

ifeelfree

粉丝: 0
资源: 1

WorldView-2多角度多时相遥感图像超分辨率重建操作方法

炫酷CSS3 3D折叠二级下拉菜单代码

图片数据集

html实现模拟手机信号强度.zip

多角度遥感影像超分辨率重建：动态上采样滤波深度网络的应用

基于稀疏编码的图像超分辨率复原.pdf

高光谱图像超分辨率的可分离光谱卷积和起始网络

基于改进卷积神经网络的单幅图像超分辨率重建方法.pdf

基于深度学习的图像超分辨率重建技术的整理_版本二.pdf

基于深度学习的图像超分辨率重建技术的研究_思维导图.pdf

Rossi.zip_图像超分辨_超分辨_超分辨率_超分辨率 matlab_超分辨重建

最新资源