"控制系统数学模型详解：微分方程与传递函数"

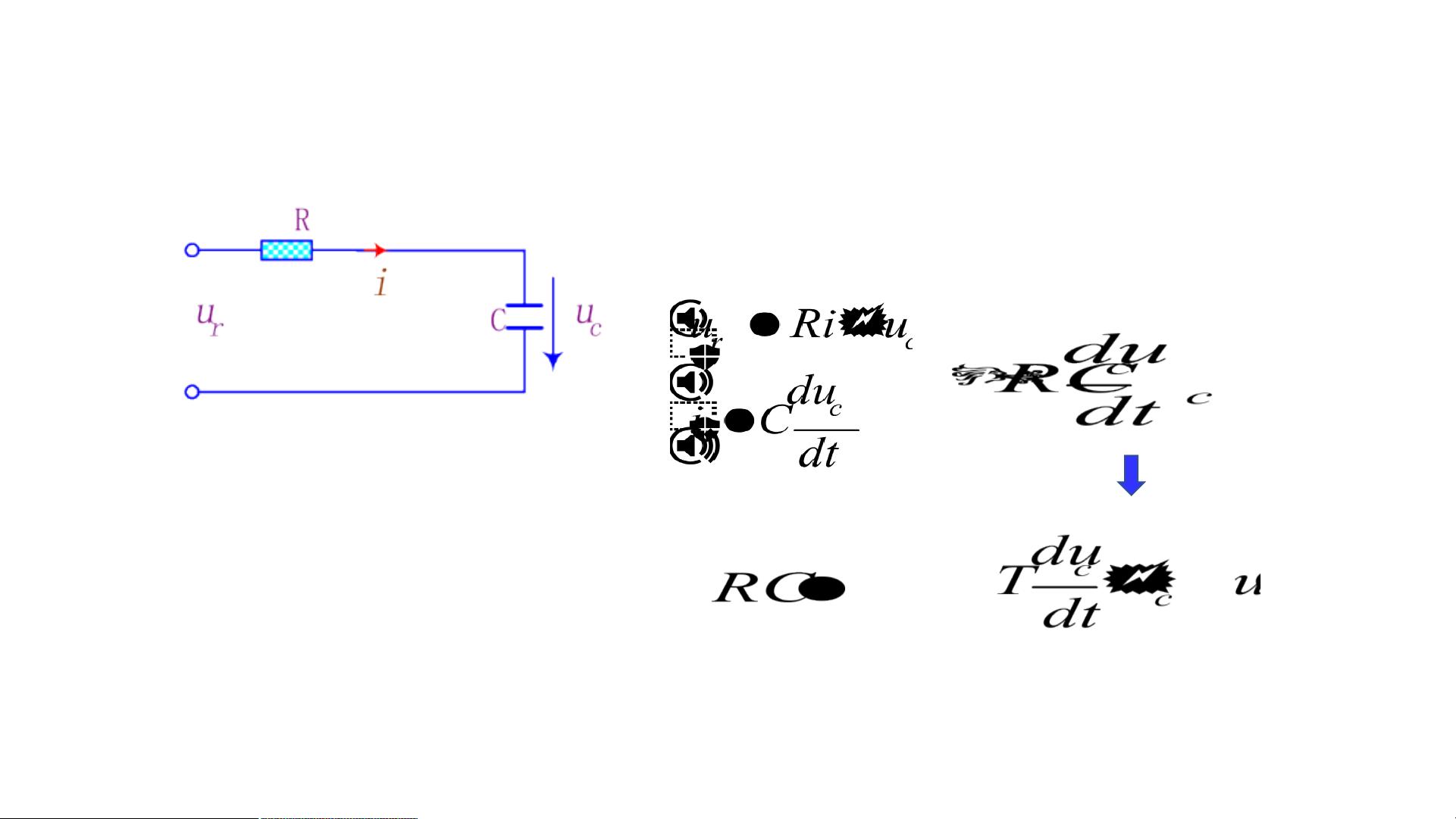
第二章是关于控制系统的数学模型的介绍。本章主要包含了几个小节，分别是控制系统的时域数学模型、复数域数学模型、动态结构图、传递函数数学模型等。其中，时域数学模型使用微分方程和差分方程来描述系统的动态行为，频率域数学模型使用传递函数来描述系统的频率特性，复数域数学模型则同时考虑了系统的时域和频域特性。 在控制系统中，我们通常需要建立数学模型来描述系统的行为。建模的方法主要有解析法和实验法。解析法是通过分析系统的物理或化学机理，列写相应的微分方程来建立数学模型。而实验法则是给系统施加某种测试信号，记录输出响应，并通过适当的数学模型来逼近系统的输入输出特性。 在建立微分方程的过程中，首先要确定系统的输入量和输出量，然后根据元部件所遵循的物理或化学定律，列写相应的微分方程。接着，我们可以消去中间变量，得到输入输出之间关系的微分方程。最后，我们可以对微分方程进行标准化处理，将与输出量相关的项写在微分方程的左端，与输入量相关的项写在右端，以便更好地进行分析和求解。 对于线性定常系统来说，微分方程的一般形式可以表示为du/dt + Au = Bu，其中u为输入量，y为输出量，A和B为常数矩阵。对于一阶线性定常连续系统来说，建立微分方程的步骤可以总结为确定输入量和输出量，根据物理或化学定律列写微分方程，消去中间变量，最后进行标准化。 在静态条件下，即变量各阶导数为零的情况下，我们可以使用静态数学模型来描述变量之间的关系，这通常是代数方程。而在动态条件下，即变量各阶导数不为零的情况下，我们需要使用动态数学模型来描述变量之间的关系，通常使用微分方程。 综上所述，控制系统的数学模型是描述系统输入量、输出量以及内部各物理量之间关系的数学表达式。常用的建模方法有解析法和实验法。微分方程是描述系统动态行为的一种数学表达方式，在线性定常系统中得到广泛应用。在建立微分方程时，确定输入量和输出量，根据系统的物理或化学定律列写微分方程，消去中间变量，进行标准化处理。通过建立数学模型，我们可以更好地理解和分析控制系统的行为。