LVPECL、LVDS、HSTL与CML间直流耦合接口详解

直流耦合
lvds
hstl
lvpecl
需积分: 46 16 下载量 91 浏览量 更新于2024-07-15 收藏 132KB PDF 举报
本篇报告深入探讨了在现代电子系统设计中，不同逻辑电平接口的关键技术——直流耦合(DC-Coupling)在四种常用差分信号标准之间的应用：LVPECL（低电压正发射极耦合逻辑）、LVDS（低电压差分信号）、HSTL（高速收发器逻辑）和CML（电流模式逻辑）。报告的焦点集中在这六种接口情况上，旨在解决这些逻辑电平在速度、电压范围以及噪声敏感性等方面的匹配问题。 首先，报告详细介绍了AC耦合作为基本隔离手段，但在高带宽系统中可能不适用，因为直流耦合提供了更好的信号完整性。针对每种信号标准，报告分别讨论： 1. **LVPECL** (LVPECL到LVPECL接口)：这部分重点阐述了如何确保低电压正偏置下的电荷泵或变压器等器件在两个LVPECL信号之间提供有效的直流耦合，以减少信号失真和噪声的影响。 2. **LVDS**：LVDS接口涉及两种情况，一是LVPECL与LVDS之间的转换，包括无芯片内终止和有终止的方案，目的是优化数据传输速率和信号质量。第二种情况是LVDS与其他逻辑电平之间的直接耦合，如LVDS到LVPECL，以兼容不同设备的驱动能力。 3. **CML**：CML逻辑以其低阻抗特性而闻名，报告会探讨LVPECL到CML的耦合策略，包括可能需要的转换电路，以适应CML的低电压工作模式。 4. **HSTL**：HSTL通常用于高速应用，报告分析了如何通过直流耦合有效地将LVPECL信号与HSTL信号同步，以实现高效的数据传输。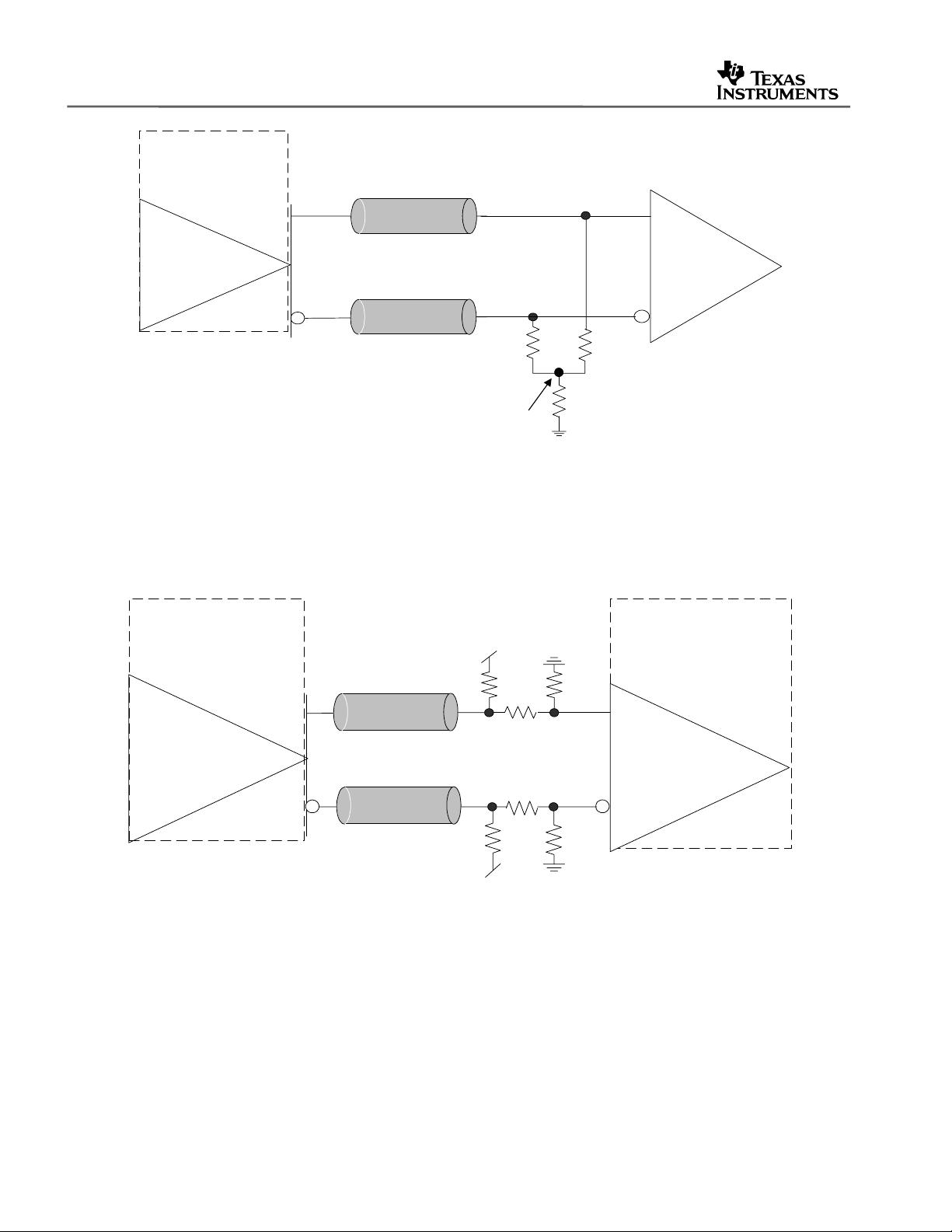 此外，报告还包含一系列图表，如输入输出参数、不同信号类型间的耦合电路示意图，帮助设计师理解每种接口的具体实现方法和注意事项。参考文献部分列出了相关的研究和标准，以便读者进一步深入学习和了解相关领域的最新进展。 这篇报告对于设计者来说是一份宝贵的资源，它提供了在实际应用中实现直流耦合，以确保不同逻辑电平之间的无缝通信和性能优化的关键技术和实践指南。

SiT9102 LVPECL / HCSL / LVDS / CML 差分高速时钟

2019-02-01 上传
于传统石英、SAW和泛音谐振技术的传统差分振荡器在稳定度和可靠度上先天不足，SiT9121系列差分振荡器采用SiTime模拟CMOS和全硅MEMS技术研发，是唯一完美结合了超高性能和可编程功能的产品，其频率稳定度达10PPM、相位抖动低于0.6ps（femtosecond），市面上目前仅SiTime实现了这两项的完美结合。 SiT9121支持1-220Mhz之间任意频率，可精确到小数点后六位，确保发挥系统的最高性能。SiT9121同时输出支持 LVDS/LVPECL，经过50000G抗冲击及70G抗振测试，MTBF（平均无故障时间）达10亿小时。SiT9121和SiT9122系 列差分振荡器定位于高性能电信、存储和网络应用，如核心和边缘路由器，SATA、SAS、光纤通道主机总线适配器，云存储、服务器、无线基站和10G 以太网**机等。此外，每款产品都支持业界标准管脚配置，不需修改设计 或布板方式即可替换现有石英差分振荡器。 SiT9121差分振荡器具备下述功能及优点： . 仅500飞秒RMS相位抖动（12kHZ至20MHz），满足SONET等应用的苛刻要求 . 总频率稳定度达±10、±25及±50PPM，系统正时余量(timing margin)更佳 . 频率范围极广：SiT9121频率范围1至220MHz，SiT9122频率范围220至650MHz . 可编程频率精度达小数点后六位，确保发挥系统最高性能 . LVPECL及LVDS信号电平可调 . 通过50000G抗冲击及70G抗振测试，MTBF（平均无故障时间）达10亿小时，高稳定度应用首选 . 工作电压2.5V、3.3V均可 . 支持工业（-40至+85°C）及长时间商业（-20至+70°C）工作温度范围 . 业界标准针脚规格3.2×2.5mm，5.0×3.2mm，7.0×5.0mm封装 . 样品24小时内发货，生产前置时间仅2至4周 . FPGA产品首选高性能差分时钟振荡器 . 兼容工业标准封装: 3.2×2.5, 5.0×3.2 and 7.0×5.0 mmxmm . 超强抗震动、抗冲击能力，优异的温漂性能 . 如需220MHz以上频点的高性能差分晶振，推荐选择SiT9122系列

使用 MATLAB 改变mimo无线通信设计

2018-05-11 上传
第 1 部分：技术与设计 简要了解 5G 物理层以及可用来优化频谱效率和数据传输速率的射频技术。 第 2 部分：新架构和算法 了解混合波束成形、线性化功率放大器、新无线波形、极化码和 LDPC 信道编码等技术。 第 3 部分：加速原型开发和现场试验 参见转换 MATLAB 参考算法以自动生成 HDL 代码的步骤。阅读有关华为和爱立信如何使用这些方法的案例研究。 第 4 部分：系统验证和测试 了解如何使用 MATLAB 借助软件无线电和 RF 仪器执行空中传输测试，对大量的测试数据进行后处理分析和可视化。

AC_Coupling_Between_Differential_LVPECL,_LVDS,_HSTL_and_CML(From_TI).pdf

2020-11-09 上传
This report provides a quick reference of ac-coupling techniques for interfacing between different logic levels. The four differential signaling levels found in this report are low-voltage positive-...

dc-coupling between differential lvpecl, lvds, hstl, and cml, texas instrume

2023-09-04 上传
在差分 LVPECL、LVDS、HSTL 和 CML 之间实现 DC 耦合可以提供更好的信号传输和接收性能。 差分 LVPECL（Low Voltage Positive Emitter Coupled Logic）是一种高速差分信号传输电标准，通常用于高速数据通信和时钟...

matlab2016代码-coupling_matrix_filter_synthesis:耦合矩阵法合成微波滤波器

2023-07-08 上传
### 回答1： 耦合矩阵法合成微波滤波器是一种利用耦合矩阵进行...MATLAB 2016的coupling_matrix_filter_synthesis代码提供了一个方便、快速和准确的工具，帮助工程师们设计和优化滤波器，提高滤波器的性能和可靠性。

class LinearMaskedCoupling(nn.Module): """ Coupling Layers """ def __init__(self, input_size, hidden_size, n_hidden, mask, cond_label_size=None): super().__init__() # stored in state_dict, but not trained & not returned by nn.parameters(); similar purpose as nn.Parameter objects # this is because tensors won't be saved in state_dict and won't be pushed to the device self.register_buffer('mask', mask) # 0,1,0,1 # scale function # for conditional version, just concat label as the input into the network (conditional way of SRMD) s_net = [nn.Linear(input_size + (cond_label_size if cond_label_size is not None else 0), hidden_size)] for _ in range(n_hidden): s_net += [nn.Tanh(), nn.Linear(hidden_size, hidden_size)] s_net += [nn.Tanh(), nn.Linear(hidden_size, input_size)] self.s_net = nn.Sequential(*s_net) # translation function, the same structure self.t_net = copy.deepcopy(self.s_net) # replace Tanh with ReLU's per MAF paper for i in range(len(self.t_net)): if not isinstance(self.t_net[i], nn.Linear): self.t_net[i] = nn.ReLU() def forward(self, x, y=None): # apply mask mx = x * self.mask # run through model log_s = self.s_net(mx if y is None else torch.cat([y, mx], dim=1)) t = self.t_net(mx if y is None else torch.cat([y, mx], dim=1)) u = mx + (1 - self.mask) * (x - t) * torch.exp( -log_s) # cf RealNVP eq 8 where u corresponds to x (here we're modeling u) log_abs_det_jacobian = (- (1 - self.mask) * log_s).sum( 1) # log det du/dx; cf RealNVP 8 and 6; note, sum over input_size done at model log_prob return u, log_abs_det_jacobian 帮我解析代码

2023-07-13 上传
在__init__方法中，首先调用父类nn.Module的构造函数super().__init__()。然后使用register_buffer方法注册了一个名为mask的缓冲区（buffer），用于存储掩码。这样做的目的是将mask保存在模型的state_dict中，但不...

\begin{array}{l}\dot{x}=\gamma\left(\mu-r^{2}\right)\left(x-\mu_{1}\right)-\omega\left(y-\mu_{2}\right)-a_{i j} x_{j} \\\dot{y}=\gamma\left(\mu-r^{2}\right)\left(y-\mu_{2}\right)+\omega\left(x-\mu_{1}\right)-a_{i j} y_{j} \\r=\sqrt{\left(x-\mu_{1}\right)^{2}+\left(y-\mu_{2}\right)^{2}}\end{array} Here, x and y are oscillator outputs and 𝛾 is the convergence rate. √𝜇 and 𝜔 indicate the amplitude and frequency, respectively. 𝜇1 and 𝜇2 are feedback parameters. 𝑎𝑖𝑗 is also represent the coupling weight between ith and jth oscillators. 用matlab的ode45求解上面的方程组

2023-07-22 上传
% coupling weight matrix initialConditions = [0.1; 0.2]; % initial values of x and y tspan = [0, 10]; % time span for integration [t, sol] = ode45(@(t, x) oscillatorODE(t, x, mu, gamma, omega, mu1,...

coupling_matrix_filter_synthesis-master

2023-11-08 上传
coupling_matrix_filter_synthesis-master是一个耦合矩阵滤波器综合的项目。耦合矩阵滤波器是一种用于信号处理的滤波器，它允许多个输入信号在不同的通道中通过各自的滤波器进行处理，并将它们的输出通过耦合矩阵...

RuntimeError: Could not export Python function call 'F'. Remove calls to Python functions before export. Did you forget to add @script or @script_method annotation? If this is a nn.ModuleList, add it to __constants__: E:\bolang\yolov7-coupling\utils\activations.py(65): forward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(860): _slow_forward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(887): _call_impl E:\bolang\yolov7-coupling\models\common.py(112): fuseforward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(860): _slow_forward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(887): _call_impl E:\bolang\yolov7-coupling\models\yolo.py(744): forward_once E:\bolang\yolov7-coupling\models\yolo.py(707): forward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(860): _slow_forward E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\nn\modules\module.py(887): _call_impl E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\jit\_trace.py(934): trace_module E:\anaconda\envs\pytorch-1.8.1\lib\site-packages\torch\jit\_trace.py(733): trace E:\bolang\yolov7-coupling\utils\torch_utils.py(363): __init__ E:\bolang\yolov7-coupling\detect.py(39): detect E:\bolang\yolov7-coupling\detect.py(196): <module>

2023-07-24 上传
这个错误是由于在导出模型时出现了问题。错误信息中提到了一个名为'F'的 Python 函数调用，但没有添加 `@script` 或 `@script_method` 注释。如果这是一个 `nn.ModuleList`，请将其添加到 `__constants__` 中。...

针对蛇形机器人，建立6个关节的结构。对蛇形机器人建立基于Hopf振荡器的模型，关节之间具有耦合性\begin{array}{l}{\left[\begin{array}{c}\dot{x}{i} \\dot{y}{i}\end{array}\right]=\left[\begin{array}{cc}\alpha\left(A_{i}^{2}-r_{i}^{2}\right) & -\omega_{i} \\omega_{i} & \alpha\left(A_{i}^{2}-r_{i}^{2}\right)\end{array}\right]\left[\begin{array}{l}x_{i} \y_{i}\end{array}\right]} \+\sum_{j=i \pm 1} h\left[\begin{array}{ll}\cos \left(\Delta \beta_{i j}\right) & -\sin \left(\Delta \beta_{i j}\right) \\sin \left(\Delta \beta_{i j}\right) & \cos \left(\Delta \beta_{i j}\right)\end{array}\right]\left[\begin{array}{l}x_{j} \y_{j}\end{array}\right] \{\left[\begin{array}{l}x_{i} \y_{i}\end{array}\right]=\left[\begin{array}{l}x_{i} \y_{i}\end{array}\right]+\left[\begin{array}{l}\dot{x}{i} \\dot{y}{i}\end{array}\right] \mathrm{d} t}\end{array}并给出耦合hopf的matlab完整代码

2023-07-22 上传
coupling_term = coupling_term + h * [cos(delta_beta), -sin(delta_beta); sin(delta_beta), cos(delta_beta)] * [x(j); y(j)]; end % 计算每个关节的加速度 acceleration = alpha * (A^2 - (x(i)^2 + y(i)^...
tianyi19901
  • 粉丝: 2
  • 资源: 7
上传资源 快速赚钱

最新资源