支持向量机(SVM)入门解析：三层理解境界

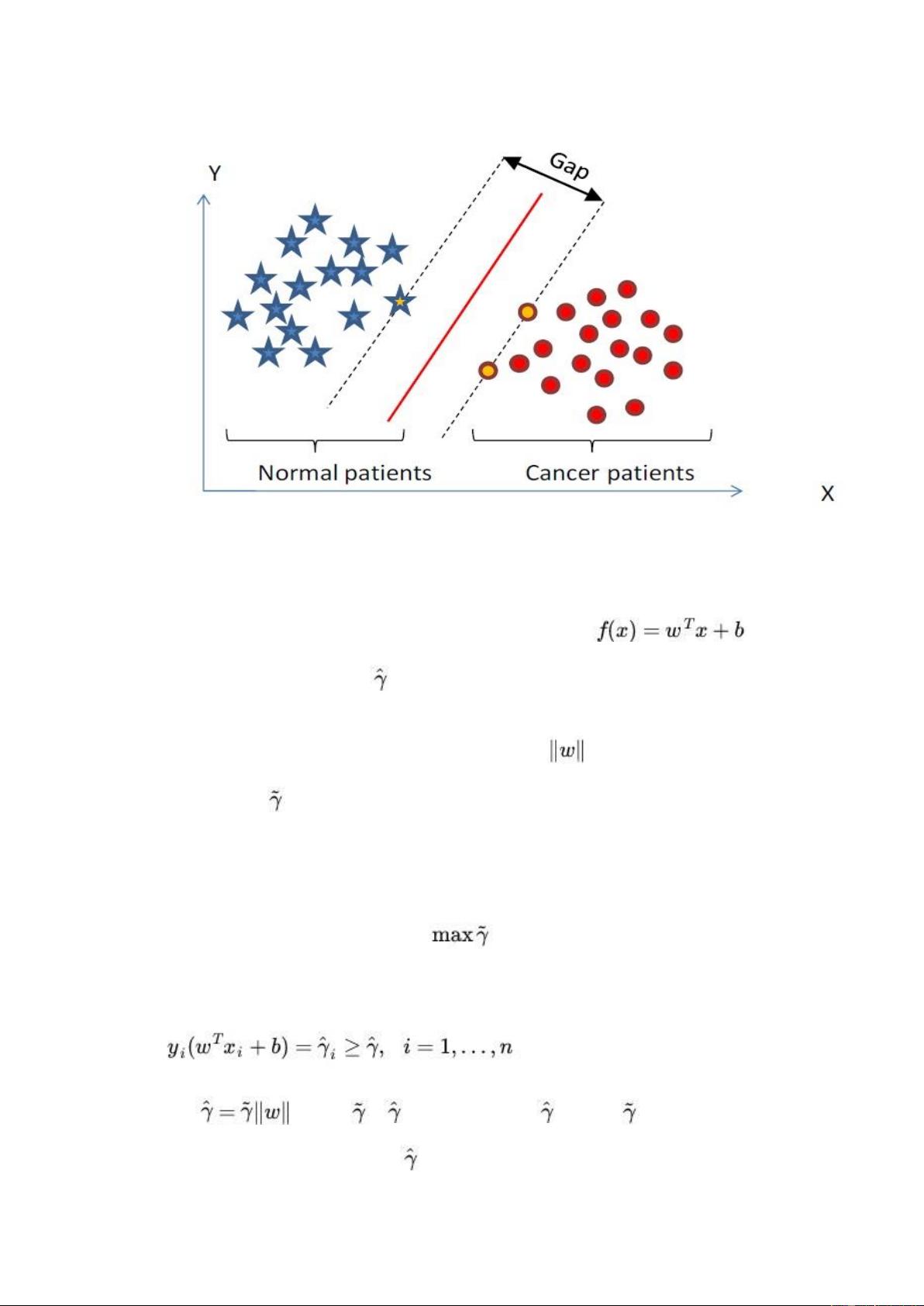
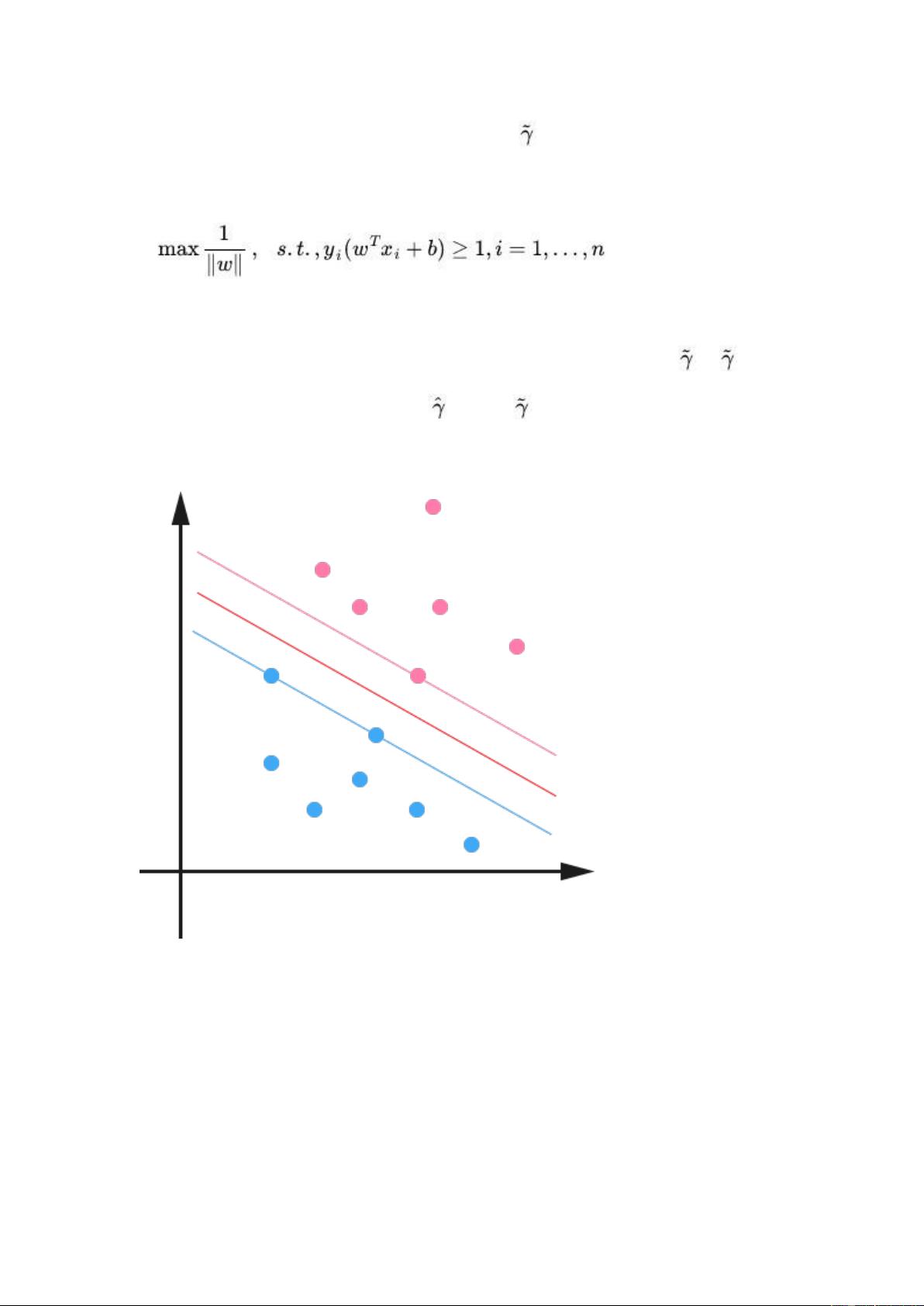
"支持向量机通俗导论，机器学习基础，深入浅出介绍SVM" 支持向量机（Support Vector Machine，SVM）是一种强大的监督学习算法，由Corinna Cortes和Vapnik在1995年提出，主要用于小样本、非线性和高维数据的分类与回归任务。SVM的核心思想是构建一个能够将不同类别数据最大程度分离的决策边界，这一边界被称为最大间隔超平面。 1.0 了解SVM SVM最初是为了解决分类问题，它学习一个分类函数或模型，该模型能够在新的未知数据上进行预测。它属于监督学习的一种，这意味着在训练过程中需要已知的输入-输出对（即训练样本）。SVM旨在找到一个能够最大化两类样本间间隔的分类器，这有助于提高模型的泛化能力，即使在数据量有限的情况下也能表现良好。 1.1 SVM的基本模型 SVM的基本模型是特征空间中的线性分类器，它的目标是找到一个超平面，使得各类别的样本点到这个超平面的距离最大。距离最大的定义是间隔（Margin），而支持向量是离超平面最近的那些样本点，它们决定了超平面的位置。 2.0 SVM的优化过程 SVM的优化问题通常转换为一个凸二次规划问题，这样可以确保找到全局最优解。通过拉格朗日乘子法，引入惩罚项来处理可能存在的误分类样本，这些样本称为支持向量。 3.0 非线性分类 对于非线性可分的数据，SVM使用核函数（如高斯核、多项式核等）进行映射，将原始数据转换到一个高维空间，在这个新空间中，原本难以划分的数据可能变得线性可分。核函数的选择对SVM的性能有很大影响。 4.0 SVM在回归任务中的应用 除了分类，SVM还可以用于回归分析，即预测连续变量。这时，SVM变体如ε-支持向量回归（ε-SVR）被使用，目标是最小化预测值与真实值之间的误差。 5.0 SVM的优势与局限 SVM的优势在于其对小样本和高维数据的良好处理能力，以及在处理非线性问题时的灵活性。然而，它可能在大数据集上计算效率较低，且选择合适的核函数和参数调整也是一个挑战。 6.0 学习与实践 理解SVM涉及数学概念，如凸优化、几何间隔和核函数等。深入学习SVM需要掌握这些基础知识，并通过实际操作和练习来加深理解。推荐使用Chrome等支持LaTeX的浏览器阅读相关文档，以便更好地理解公式和推导过程。 支持向量机是一种强大且灵活的机器学习工具，尤其适用于分类和回归任务。通过最大化间隔和利用核函数，SVM能在多种复杂情况下实现高效准确的预测。对于想要掌握SVM的人来说，理论结合实践是关键，不断探索和实验将帮助你更深入地理解这一算法。