二阶系统时域分析：性能指标与瞬态响应

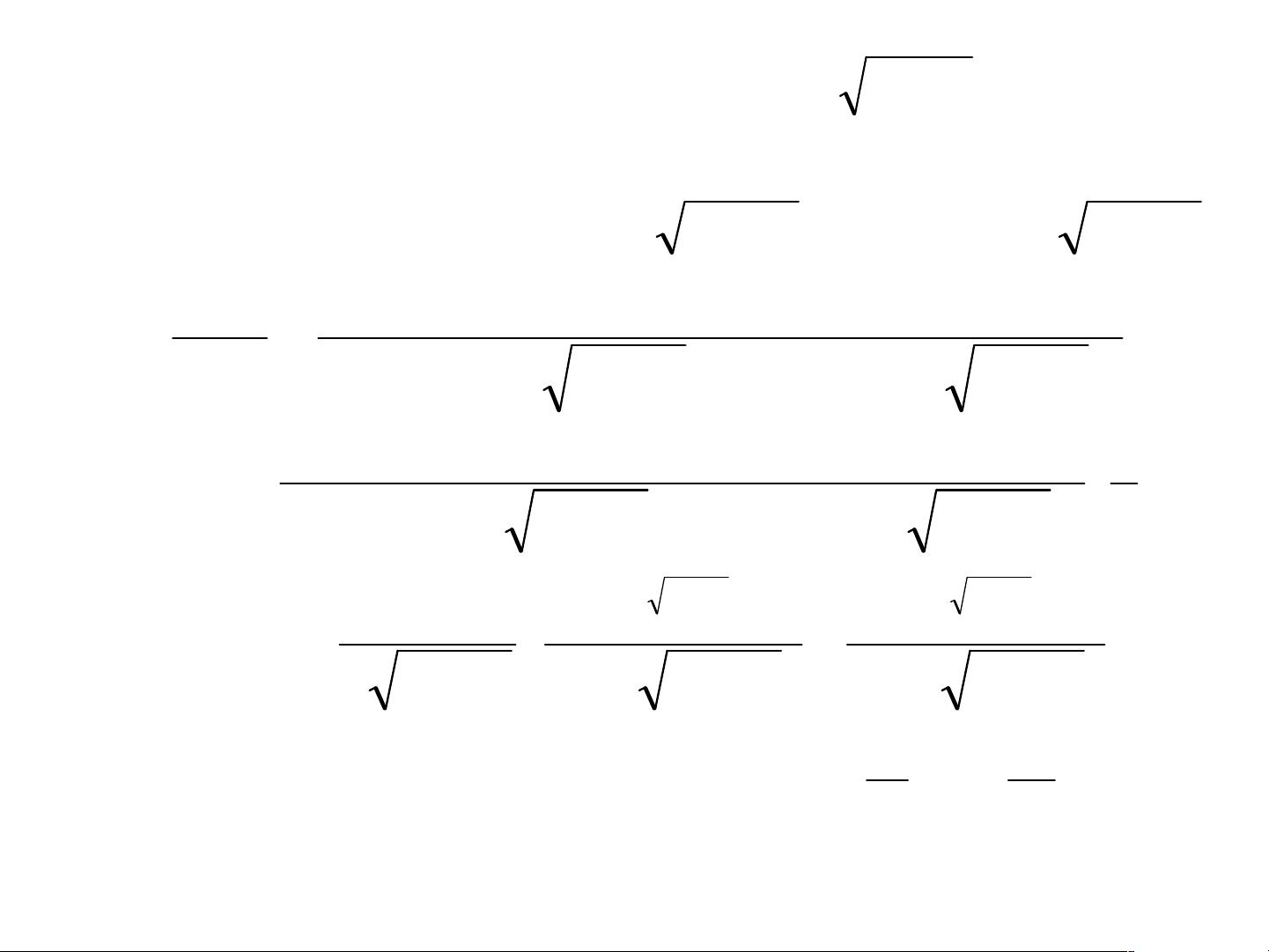
“自动控制原理：第3章 第3讲 二阶系统的时域分析.ppt” 本文主要讨论了自动控制原理中的一个重要主题——二阶系统的时域分析。二阶系统在许多工程应用中非常常见，因为许多高阶系统可以通过简化模型转化为二阶系统。时域分析是评估系统性能的重要手段，尤其是对于瞬态响应和稳定性。 一、二阶系统的数学模型与性能指标 二阶系统的典型结构通常包括一个二阶微分方程，其开环传递函数表示为： \[ G(s) = \frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2} \] 其中，\( \omega_n \) 是无阻尼振荡频率，\( \zeta \) 是阻尼系数。闭环传递函数可以通过开环传递函数和反馈信号计算得到。二阶系统的特征根（闭环极点）是决定系统动态行为的关键，由特征方程： \[ s^2 + 2\zeta\omega_n s + \omega_n^2 = 0 \] 确定。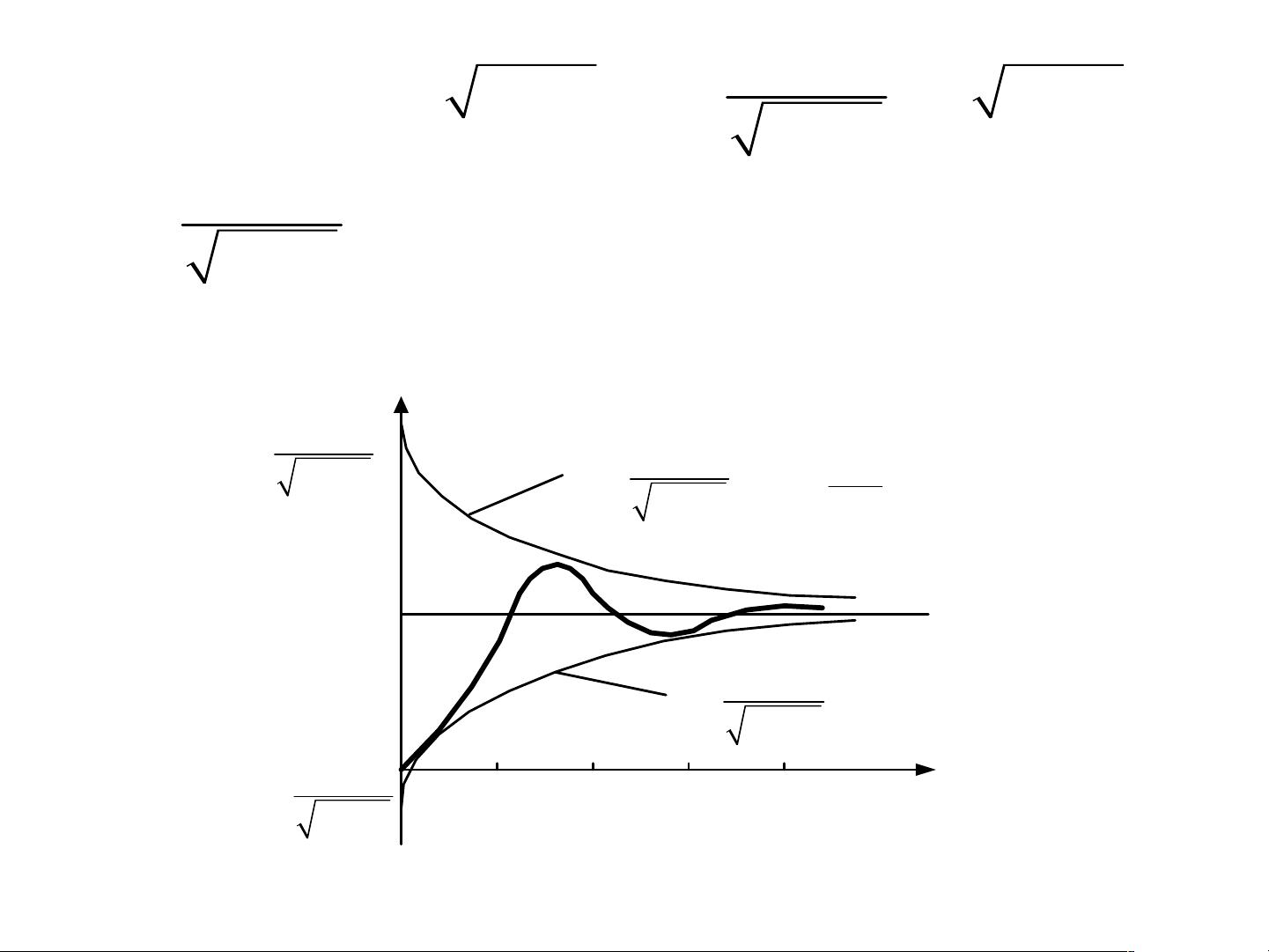 二、二阶系统的瞬态响应与性能指标 1. 零阻尼系统（\( \zeta = 0 \)）：特征根为一对共轭虚根，系统表现为等幅振荡。 2. 欠阻尼系统（\( 0 < \zeta < 1 \)）：特征根为一对负实部的共轭复根，系统呈现衰减的振荡。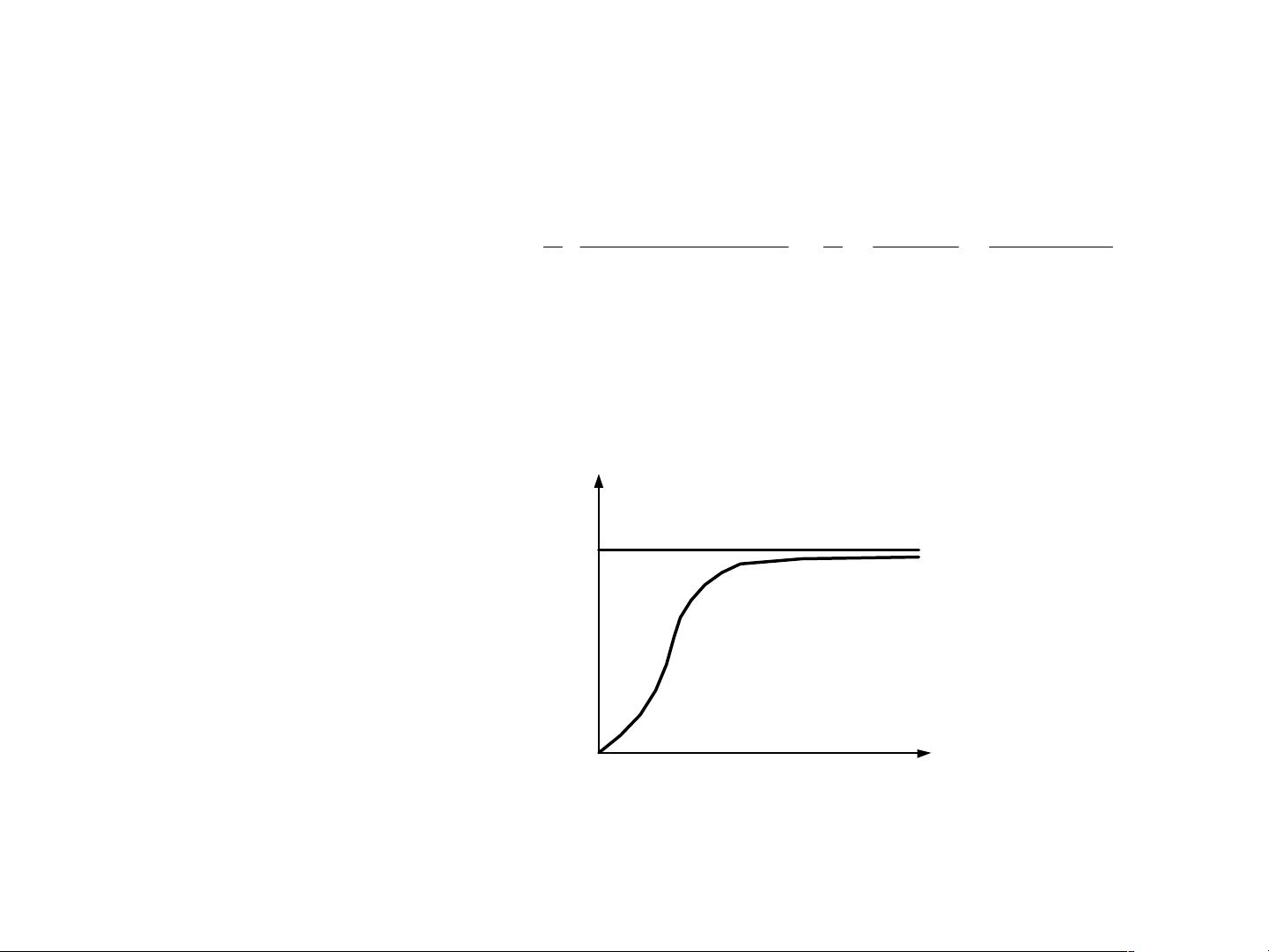 3. 临界阻尼系统（\( \zeta = 1 \)）：特征根为一对相等的实根，系统无振荡，阶跃响应线性上升至稳态值。 4. 过阻尼系统（\( \zeta > 1 \)）：特征根为一对不等的负实根，系统无振荡，阶跃响应以非振荡方式达到稳态值。 5. 不稳定系统（\( \zeta \) 或 \( \omega_n \) 的特定组合导致极点位于右半平面）：特征根可能为正实部或共轭复根，系统表现为发散的振荡或非振荡过程。 二阶系统的性能指标通常包括上升时间、超调量、调整时间、峰值时间等，这些指标用于评估系统的快速性、稳定性和精度。 三、单位阶跃响应 当输入为单位阶跃函数时，系统的输出可以通过闭环传递函数计算。在不同的阻尼条件下，二阶系统的阶跃响应有着显著的差异，从无振荡的线性上升到衰减或发散的振荡模式。 总结来说，二阶系统的时域分析是理解和设计自动控制系统的基础，通过调整阻尼系数和无阻尼振荡频率，可以优化系统的动态性能以满足具体应用的需求。理解这些基本概念对于控制系统的设计和分析至关重要。