MATLAB计算方法实例：二分法与牛顿迭代法

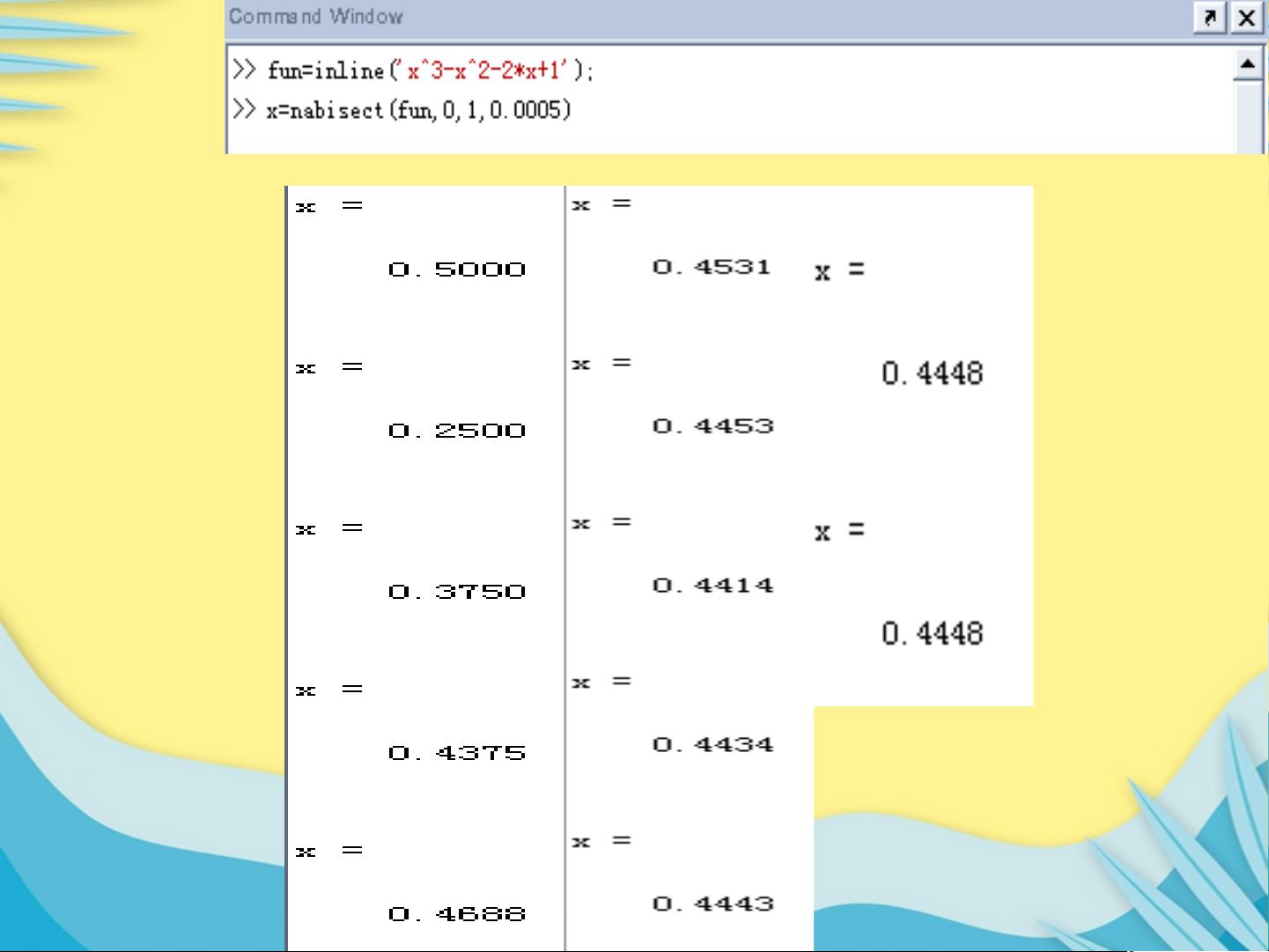
"该资源为MATLAB实例讲解的PPT文档，主要涵盖了计算方法中的关键算法实现，包括二分法、牛顿迭代法以及LU分解。文档提供了详细的MATLAB代码示例，帮助学习者理解并应用这些算法。" 在计算方法的学习中，MATLAB是一种常用的工具，它能够方便地实现各种数值计算算法。以下是对PPT文档中提到的几个关键知识点的详细解释： 1. **二分法（Bisection Method）**： 二分法是一种寻找函数零点的迭代算法。在给定一个连续函数`fname`和包含零点的初始区间 `[a, b]`，如果`fa*fb < 0`（即函数在区间的两个端点取相反符号），那么零点一定位于这个区间内。二分法不断将区间对半分，直到区间长度小于给定的精度`e`。在MATLAB中，这一过程通过循环实现，每次迭代都将当前区间的中点`x=(a+b)/2`作为新的区间边界。 2. **牛顿迭代法（Newton's Method）**： 牛顿迭代法用于求解方程`f(x) = 0`。它基于牛顿-拉弗森公式 `x_new = x_old - f(x_old) / f'(x_old)`，其中`f'(x)`是`f(x)`的导数。在MATLAB程序中，设定迭代次数`N`和精度`e`，当迭代次数达到上限或误差小于给定精度时停止迭代。每个迭代步骤都会更新变量`x0`，直至找到满足条件的解。 3. **回代（Backward Substitution）**： 回代是解决线性方程组`Ax=b`的一个步骤，特别是在已知矩阵`A`为下三角矩阵时。从最后一个方程开始，依次求解每个未知数`x(n)`，然后向前递推至第一个未知数。MATLAB代码展示了如何进行回代计算，通过一个`for`循环逐行解决方程。 4. **LU分解（LU Factorization）**： LU分解是将一个方阵`A`分解为一个下三角矩阵`L`和一个上三角矩阵`U`的乘积，即`A = LU`。在MATLAB中，`nalu`函数接收一个可逆方阵`a`，并返回`L`和`U`。通过初始化`L`为单位矩阵，逐步将`a`的每一行转换为下三角和上三角形式。 这些MATLAB实例旨在帮助学生理解并实际操作计算方法中的基本算法，从而提高他们解决问题的能力。通过阅读和运行这些代码，学习者可以更好地掌握二分法、牛顿迭代法和LU分解的原理，并能够应用到实际的数值计算问题中。