GPU加速的DPSO-RE算法：考虑VSI非线性的表面PMSM参数识别

11 浏览量更新于2024-08-26 收藏 1.77MB PDF 举报

"这篇论文探讨了考虑电压源逆变器（VSI）非线性因素的表面永磁同步电机（SPMSM）参数识别问题。文章提出了一种结合动态粒子群优化（DPSO）与接收编辑（RE）策略的算法，即G-DPSO-RE，用于寻找参数估计的最优解。此算法在图形处理单元（GPU）上实现了加速，以提高参数估计的效率。在G-DPSO-RE中，动态劳动分工策略被引入到群体进化过程中，并依据进化因子调整。同时，文章对运动方程进行了创新性修改，以更新粒子速度。此外，还发展了一种基于混沌逻辑的免疫RE操作符，以助于全局最佳个体（gBest粒子）寻找更优区域。该方法利用GPU的并行计算能力加速参数估计，实现在VSI非线性影响下的SPMSM参数和干扰电压（Vdead）的同时估计。实验数据表明，该方法对于考虑VSI非线性影响的参数估计是有效的，并分析了VSI非线性对参数估计精度的影响。" 本文的研究重点在于解决SPMSM参数识别中的非线性问题，特别是VSI非线性对电机性能的影响。VSI非线性可能导致电机参数估计的不准确，从而影响电机的控制性能和效率。作者首先建立了考虑VSI非线性的SPMSM精确参数估计模型，这是理解和改善电机性能的基础。接下来，他们提出了G-DPSO-RE算法，这是一种优化工具，结合了DPSO和RE策略的优势。DPSO是一种全局优化算法，能有效地搜索多维空间的最优解。通过与RE策略的融合，G-DPSO-RE能够更有效地探索参数空间，寻找最优参数估计。同时，动态劳动分工策略增强了算法的探索能力，适应性地调整粒子的搜索行为。而基于混沌逻辑的免疫RE操作符进一步促进了全局最优解的发现，提高了算法的全局寻优能力。为了提高计算效率，G-DPSO-RE算法在GPU上实现了并行化。GPU并行计算技术能够显著加速参数估计过程，使得在处理大量数据时，算法的执行时间大大缩短。这在实时或大规模的参数估计任务中尤为重要。实验部分，作者使用实际电流和转子速度数据验证了该方法的有效性，尤其是在处理由VSI非线性导致的干扰电压Vdead的估计。通过分析，他们展示了VSI非线性如何影响参数估计的精度，并讨论了如何通过改进的算法来减轻这种影响。该研究通过提出G-DPSO-RE算法，为考虑VSI非线性的SPMSM参数识别提供了一个高效且准确的解决方案。这种方法不仅提升了参数估计的精度，还通过GPU并行计算技术实现了计算效率的提升，为未来类似的电机控制和参数识别问题提供了有益的参考。

1336 IEEE JOURNAL OF EMERGING AND SELECTED TOPICS IN POWER ELECTRONICS, VOL. 5, NO. 3, SEPTEMBER 2017

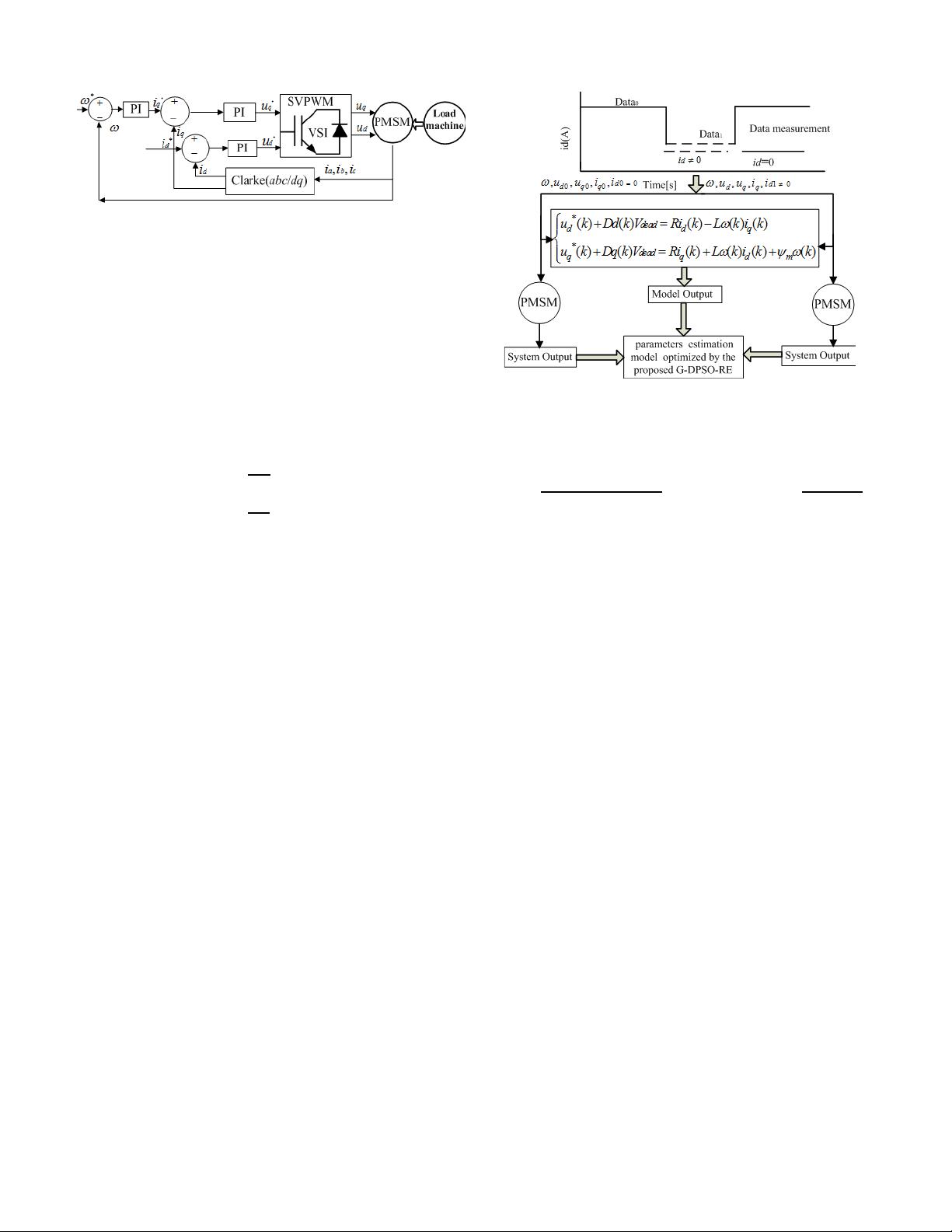
Fig. 1. Schematic of vector controlled PMSM drive system.

analysis are given in Section IV. Finally, conclusions are

summarized in Section V.

II. PMSM M

ODEL AND DESIGN OF PARAMETER

ESTIMATION MODEL

A. PMSM Model

The mathematical model of the PMSM in dq-axis voltage

equation is given as

⎧

⎪

⎨

⎪

⎩

= Ri

+ L

− L

ωi

= Ri

+ L

ωi

+ ψ

(1)

where ω is the electrical angular velocity, u

, u

, i

,andi

are dq-axis stator voltage and current. The elements of the

parameter set{R, L

, L

, ψ

} are the motor winding resis-

tance, magnet ﬂux, d-axis and q-axis inductances, respectively,

which are usually unknown to the users. Note that the esti-

mated resistance R, as a lumped circuit resistance, includes

two parts, namely, the

ON-state slope resistances of the active

switch and freewheeling diode in inverter and terminal wire

resistance. At steady state the (1) can be discretized as follows:



(k) = Ri

(k) − L

ω(k)i

(k)

(k) = Ri

(k) + L

ω(k)i

(k) + ψω(k).

(2)

In a PMSM vector control system, the voltages used for the

PMSM parameter estimation are usually measured from the

output voltage of the current controllers, and the terminal

voltages of PMSM are PWM pulses from VSI which are dif-

ﬁcult to measure directly [22]–[24]. The two output voltages,

denoted by u

∗

and u

∗

,areshowninFig.1.Notethatthere

exists an error between the reference voltage of the controller

and the actual output voltage of the VSI due to the nonlinearity

of VSI, so it is essential to estimate VSI nonlinearity.

Taking into account the inﬂuence of VSI nonlinearity,

the model of PMSM and VSI as a whole, for surface-mounted

PMSM, d-axis inductance is regarded as equal to q-axis

inductance, that is L

= L

= L, (2) can be rewritten as

∗

(k) + D

(k)V

dead

= Ri

(k) − Lω(k)i

(k) (3a)

∗

(k) + D

(k)V

dead

= Ri

(k) + Lω(k)i

(k) + ψ

ω(k)

(3b)

where D

and D

are the function of rotor position [13],

in (3) L, R, ψ

and V

dead

are the parameters to be estimated.

The variable V

dead

is the distorted voltage due to VSI

Fig. 2. Schematic of estimation and mathematical model.

nonlinearity, and can be represented as

dead

+ T

− T

OFF

· (V

−V

sat

+ V

) +

sat

+ V

(4)

where T

dead

is the dead-time period of the switching device,

and T

OFF

are turn-ON and turn-OFF times of the switching

device, V

is measured real-time dc bus voltages, V

sat

and V

are the saturation voltage drop of the active switch and the

forward voltage drop of the freewheeling diode, T

is the

switching period. It can be seen that if variable V

dead

ignored, the estimation results may also be inﬂuenced by the

nonzero VSI nonlinearity terms (D

· V

dead

and D

· V

dead

and this may introduce an error into the estimation of the

PMSM parameters.

B. Design of Estimation Model Based

on Parameter Optimization

Apparently, the rank of (3) <3, while the number of

unknown parameters is four, thus the (3) is rank deﬁcient,

the four parameters in (3) are not be identiﬁable and an

estimate to converge to suboptimal. To solve this problem,

a full rank reference model should be constructed if all these

parameters need to be estimated simultaneously at steady state.

Generally, d-axis current injection method is employed to

obtain more state equations due to the variation of d-axis

current. The parameters of machine can be assumed to be

constant as the duration of injected pulse current is very short

due to mechanical inertia and fast response of current loop PI

controller. In this case, the inﬂuence of injecting a short pulse

of i

on output torque and speed can be negligible. Thus,

the two sets of steady state data (Data0 and Data1) can be

used together for the estimation machine parameters and VSI

nonlinearity simultaneously modeling. An illustration is given

in Fig. 2, where i

= 0 (A) during normal operation for the

decoupling the ﬂux and torque control of SPMSM, and a very

short time of i

= 0 (A) is injected to obtain another dq-axis

voltage equation model. Two groups of equations at i

= i

剩余11页未读，继续阅读

weixin_38701952

粉丝: 5
资源: 977

GPU加速的DPSO-RE算法：考虑VSI非线性的表面PMSM参数识别

基于带有学习策略的动态PSO的VSI馈送PMSM的参数估计

基于python的垃圾分类系统资料齐全+详细文档.zip

基于java的网上书城系统设计与实现.docx

基于Go语言Gin框架的订单管理系统，正在建设中，本身为简单Demo，有助于掌握Go语言语法以及Gin开发框架简单使用，喜欢就点个Star吧！.zip

mumu多开器软件电脑

河南某211研究生期末算法设计分析期末复习

基于Python3的Scrapy网页爬虫框架详细文档+资料齐全.zip

Android -「安卓端」 广告配音工具用于语音合成助手/自媒体配音/广告配音/文本朗读

MyBatis-Flex 一个优雅的 MyBatis 增强框架

基于Python医疗机构药品及耗材信息管理系统带vue前后端分离毕业源码案例设计资料齐全+详细文档.zip

最新资源

Android -「安卓端」广告配音工具用于语音合成助手/自媒体配音/广告配音/文本朗读