重要性采样在图形学与深度学习中的应用

需积分: 9 64 浏览量更新于2024-07-15 收藏 643KB PDF 举报

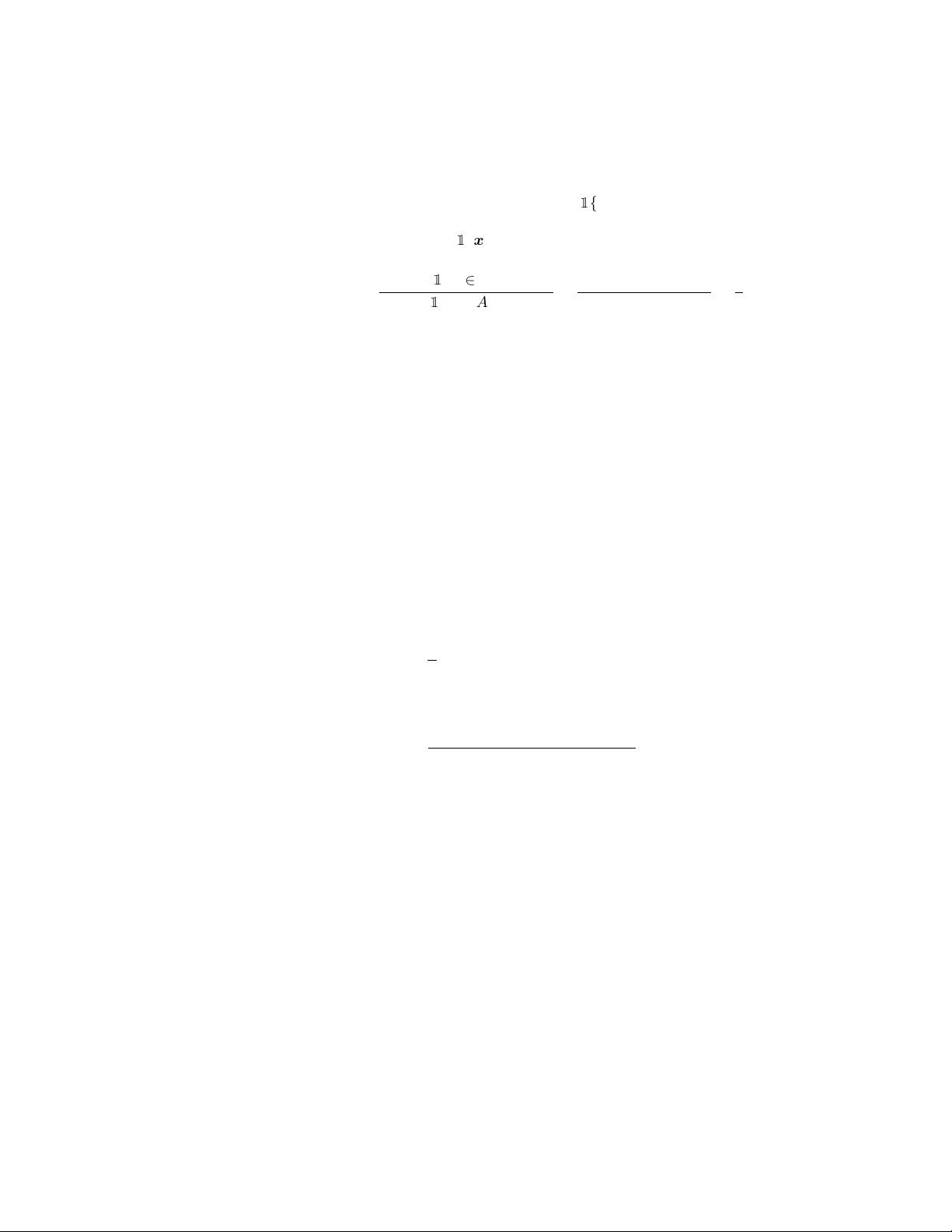
"importance sampling.pdf - 一种关键的采样技术，适用于图形学和深度学习领域" 在计算科学和统计模拟中，重要性采样（Importance Sampling）是一种非常关键的技术，尤其对于处理那些目标函数在特定区域值极小但概率分布较低的问题时尤为有效。这种技术广泛应用于高能物理、贝叶斯推断以及稀有事件模拟等多个领域。在图形学中，它可以帮助提高光线追踪等复杂场景的渲染效率；在深度学习中，它能优化采样效率，加速训练过程。 9.1 基本的重要性采样基本的重要性采样方法涉及到重新定义样本的生成过程，通过选择一个辅助分布，使得辅助分布下的目标函数更集中，从而减少无效样本的生成。这个辅助分布通常是目标分布的变形，目的是让更多的采样落在我们感兴趣的区域A内。 9.2 自归一化的重要性采样自归一化的重要性采样（Self-normalized Importance Sampling）是一种特殊的形式，它不需要知道原分布的总体概率，而是通过对同一辅助分布下采样的样本进行归一化来估计期望值。 9.3 重要性采样诊断为了确保采样效率和准确性，我们需要对重要性采样进行诊断，包括检查样本的多样性、有效样本数量以及分布的匹配程度等。 9.4 PERT（Program Evaluation and Review Technique）例子 PERT是一个项目管理工具，通过重要性采样可以对项目的不确定性进行建模和分析，例如估算任务完成时间的分布。 9.5 重要性采样与接受-拒绝法接受-拒绝法是另一种常用的模拟方法，但在处理稀有事件或低概率区域时可能效率低下。重要性采样提供了一种更有效的方法，因为它可以直接在感兴趣的区域内采样。 9.6 指数倾斜指数倾斜是改变分布形状的技术，用于更好地匹配目标函数的特性，从而改进采样效率。 9.7 模式和海森矩阵在寻找分布的局部最优或高概率区域时，模式和海森矩阵可以帮助我们理解和调整辅助分布，使其更适应目标函数的特性。 9.8 一般变量和随机过程重要性采样不仅可以应用于静态变量，还可以扩展到随机过程，如布朗运动或其他复杂的动态系统。 9.9 退出概率示例在模拟系统退出条件或罕见事件时，重要性采样能有效地估计这些概率，即使在系统具有复杂行为的情况下。 9.10 控制变量在重要性采样中的应用控制变量是一种策略，通过引入额外的变量来减少估计误差，它增强了重要性采样在处理多维问题时的能力。 9.11 混合重要性采样混合重要性采样结合多个辅助分布，通过优化不同分布的权重，可以进一步提升估计的精度和稳定性。 9.12 多重重要性采样多重重要性采样（Multiple Importance Sampling）允许同时使用多个采样策略，结合它们的贡献来估计期望，减少了偏差并提高了效率。 9.13 正向化正向化技术用于确保估计的无偏性，即使在某些辅助分布下采样失败时也能得到有效的估计。 9.14 “如果”模拟 "如果"模拟利用重要性采样来探索假设情景的影响，如政策变化或市场波动，以便进行预测和决策。总结来说，重要性采样是一种强大的工具，能够有效地处理复杂和稀有的概率事件，它在图形学和深度学习中的应用展现了其在计算效率和准确度方面的优势。通过理解并熟练运用这些方法，研究者和工程师可以更好地解决实际问题，提高模型性能。

8 9. Importance sampling

Example 9.3 shows that making any small change of variance will bring an

extreme likelihood ratio in d dimensions when d is large. The allowable change

to σ

decreases with d. If we take σ

= 1 + A/d

1/2

for A > −1/2 then a Taylor

series expansion of log(E

(w(X))) shows that (σ

√

2σ

− 1)

remains bounded

as d grows.

Although we can get a lot of insight from the likelihood ratio w(x) the

eﬃciency of importance sampling compared to alternatives still depends on f .

We will see another example of that phenomenon in §9.3 where we discuss some

measures of eﬀective sample size for importance sampling.

9.2 Self-normalized importance sampling

Sometimes we can only compute an unnormalized version of p, p

(x) = cp(x)

where c > 0 is unknown. The same may be true of q. Suppose that we can com-

pute q

(x) = bq(x) where b > 0 might be unknown. If we are fortunate or clever

enough to have b = c, then p(x)/q(x) = p

(x)/q

(x) and we can still use (9.3).

Otherwise we may compute the ratio w

(x) = p

(x)/q

(x) = (c/b)p(x)/q(x)

and consider the self-normalized importance sampling estimate

eµ

i=1

f(X

)

i=1

)

(9.6)

where X

∼ q are independent. The factor c/b cancels from numerator and

denominator in (9.6), leading to the same estimate as if we had used the desired

ratio w(x) = p(x)/q(x) instead of the computable alternative w

(x). As a

result we can write

eµ

i=1

f(X

)w(X

)

i=1

w(X

)

. (9.7)

Theorem 9.2. Let p be a probability density function on R

and let f(x)

be a function such that µ =

f(x)p(x) dx exists. Suppose that q(x) is a

probability density function on R

with q(x) > 0 whenever p(x) > 0. Let

, . . . , X

∼ q be independent and let eµ

be the self-normalized importance

sampling estimate (9.6). Then



lim

n→∞

eµ

= µ



= 1.

Proof. We may use expression (9.7) for eµ

. The numerator in (9.7) is the average

ˆµ

of f(X

)p(X

)/q(X

) under sampling from q. These are IID with mean µ

by (9.2). The strong law of large numbers gives P



lim

n→∞

ˆµ

= µ



= 1. The

denominator of (9.7) converges to 1, using the argument for the numerator on

the function f with f (x) ≡ 1.

The self-normalized importance sampler eµ

requires a stronger condition

on q than the unbiased importance sampler ˆµ

does. We now need q(x) > 0

whenever p(x) > 0 even if f(x) is zero with high probability.

author’s permission

9.2. Self-normalized importance sampling 9

To place a conﬁdence interval around eµ

we use the delta method and equa-

tion (2.30) from §2.7 for the variance of a ratio of means. Applying that formula

to (9.7) yields an approximate variance for eµ

Var(eµ

) =



(f(X )w(X) −µw(X))



(w(X))

q,sn

, where

q,sn

= E



w(X)

(f(X ) −µ)



(9.8)

For a computable variance estimate, we employ w

instead of w, getting

Var(eµ

) =

i=1

)

(f(x

) − eµ

)



i=1

)



i=1

(f(x

) − eµ

)

(9.9)

where w

= w

j=1

) is the i’th normalized weight. The delta

method 99% conﬁdence interval for self-normalized importance sampling is

eµ

± 2.58

Var(eµ

When the weight function w(x) is computable, then we can choose to use

either the unbiased estimate (9.3) or the ratio estimate (9.6). They each have

their strengths. Their variance formulas are:

nVar(ˆµ

) =

(f(x)p(x) − µq(x))

q(x)

dx, and

Var(eµ

) =

p(x)

(f(x) − µ)

q(x)

dx.

An argument for eµ

is that it is exact when f(x) = C is constant, while ˆµ

is not. We are not usually focused on estimating the mean of a constant, but

if we don’t get that right, then our estimates of P(X ∈ B) and P(X 6∈ B) for a

set B, won’t sum to one, and

E(f(X ) + C) won’t equal

E(f(X )) + C, both of

which could lead to strange results.

The arguments in favor of ˆµ

are that it is unbiased, has a simple variance

estimate, and the variance can be made arbitrarily close to 0 by making ever

better choices of q.

It is not possible for the self-normalized estimate eµ

to approach 0 variance

with ever better choices of q. The optimal density for self-normalized importance

sampling has the form q(x) ∝ |f (x) − µ|p(x) (Hesterberg, 1988, Chapter 2).

Using this formula we ﬁnd (Exercise 9.15) that

q,sn

> E

(|f(X ) −µ|)

. (9.10)

It is zero only for constant f(x). Self-normalized importance sampling cannot

reduce the variance by more than E

((f(X ) −µ)

)/E

(|f(X ) −µ|)

author’s permission

10 9. Importance sampling

Example 9.4 (Event probability). Let f(x) =

{x ∈ A}, so µ = E(f (X )) is

the probability of event A. The optimal distribution for self-normalized impor-

tance sampling is q(x) ∝ p(x)|

{x ∈ A} −µ|. Under this distribution

q(x) dx =

p(x)|

{x ∈ A} −µ|dx

p(x)|

{x ∈ A} −µ|dx

µ(1 −µ)

µ(1 −µ) + (1 −µ)µ

Whether A is rare or not, the asymptotically optimal density for self-normalized

importance sampling puts half of its probability inside A. By contrast, in ordi-

nary importance sampling, the optimal distribution places all of its probability

inside A.

When w(x) is computable, then a reasonable answer to the question of

whether to use ˆµ

or eµ

is ‘neither’. In this case we can use the regression

estimator of §8.9 with the control variate w(X). This variate has known

mean, E

(w(X)) = 1. The regression estimator has a bias but it cannot in-

crease the asymptotic variance compared to ˆµ

. The regression estimator has

approximate variance (1 − ρ

)σ

/n compared to σ

/n for ˆµ

of (9.3), where

ρ = Corr

(f(X )w(X), w(X)). The regression estimator is also at least as eﬃ-

cient as the ratio estimator which in this case is eµ

. The regression estimator

is exact if either q(x) ∝ f(x)p(x) (for nonnegative f ) or f is constant.

The regression estimator here takes the form

ˆµ

q,reg

i=1

f(X

)w(X

) −

β(w(X

) −1), (9.11)

where

β =

i=1

(w(X

) − ¯w)f(X

)w(X

)

i=1

(w(X

) − ¯w)

for ¯w = (1/n)

i=1

w(X

). To get both ˆµ

q,reg

and its standard error, we can

use least squares regression as in Algorithm 8.3. We regress f (X

)w(X

) on the

centered variable w(X

) − 1 and retain the estimated intercept term as ˆµ

q,reg

Most regression software will also compute a standard error se(ˆµ

q,reg

) for the

intercept. Our 99% conﬁdence interval is ˆµ

q,reg

± 2.58 se(ˆµ

q,reg

The regression estimator version of importance sampling is a very good

choice when we are able to compute w(x). It has one small drawback rela-

tive to ˆµ

. In extreme cases we could get ˆµ

q,reg

< 0 even though f(x) > 0

always holds. In such cases it may be preferable to use a reweighting ap-

proach as in §8.10. That will give ˆµ

q,reg

> 0 when min

16i6n

f(x

) > 0 and

min

16i6n

p(x

)/q(x

) < 1 < max

p(x

)/q(x

). On the other hand, getting

ˆµ

q,reg

< 0 when P(f(X ) > 0) = 1 suggests that the sampling method has not

worked well and perhaps we should increase n or look for a better q instead of

trying to make better use of the given sample values.

author’s permission

剩余45页未读，继续阅读

不负初心

粉丝: 47
资源: 17

重要性采样在图形学与深度学习中的应用

论文研究-Bayesian Maximum A Posterior DOA Estimator Based on Importance Sampling.pdf

MC Practice.zip sratchapixel

PG.pdf

randomForest.pdf

polikar2012.pdf

培训资料 SPC资料.pdf

蒙特卡洛模型方法 (2).pdf

CMU高级机器学习马尔可夫链.pdf

粒子滤波算法综述_胡士强.pdf

Sample Efficient Actor-Critic with Experience Replay.pdf

最新资源