二叉树与6-3树的存储结构及转换详解

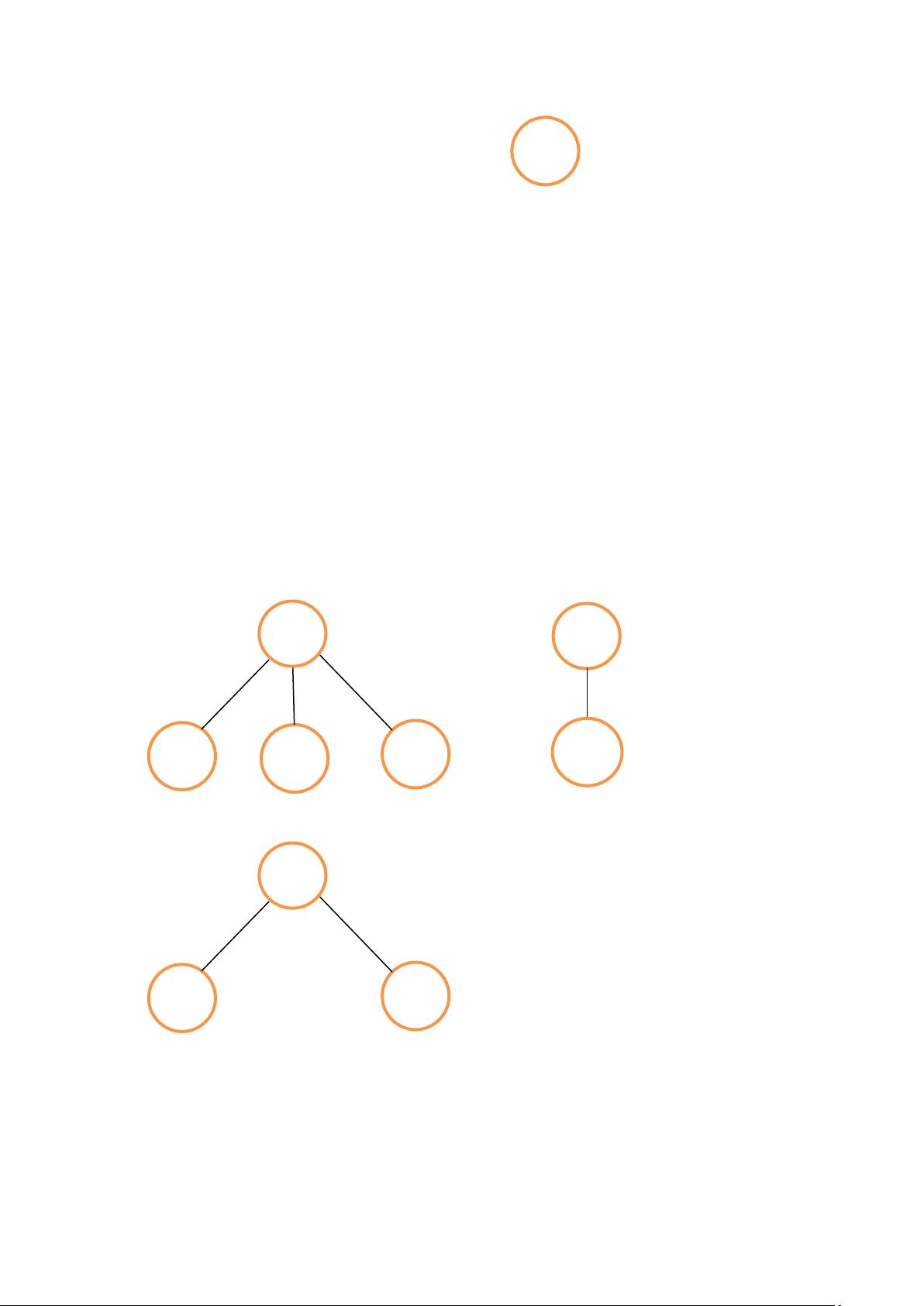
在IT领域，"6-3树和二叉树1"的主题主要讨论了树和二叉树的基本概念以及它们之间的区别，以及树的几种常见存储结构。首先，树和二叉树的区分在于二叉树对左右子树有明确的规定，而多叉树只要求区分出子树，但不一定限制为两个。二叉树是多叉树的一种特殊情况。 存储结构方面，主要有三种方法： 1. 双亲表示法：每个节点包含数据域和一个指针域，用于存储父节点的序号。这种表示法通过`PTreeNode`结构体实现，如`{DataType data; int parent;}`。`PTree`则是一个数组，用来存储所有节点及其数量。 2. 孩子链表法：每个节点只存储自身编号和指向下一个孩子的指针。通过`ChNode`结构体定义，如`{int no; ChNode* next;}`，然后用`ChTreeNode`来整合数据和孩子节点链表，以及`PTree`来管理这些节点。 3. 孩子兄弟链表法：此方法中，每个节点的左指针指向最左边的孩子，而孩子节点的右指针则指向右侧的兄弟。这样形成了一种有序的子树链接结构。 对于树和森林的转换，重点在于将非二叉树结构转换为二叉树以便于处理。树转换为二叉树的过程涉及连线（连接相邻的兄弟节点）、抹线（删除多余链接）和旋转（调整结构以符合二叉树规则）。例如，给定一个树，首先要连接相邻兄弟，然后删除其他链接，并通过旋转操作确保每个节点都有明确的左或右子树。 森林转换为二叉树则是对每个独立的树进行上述过程，然后再依次合并，形成一个具有层次关系的二叉树。例如，一个包含多棵树的森林，每棵树会先转换为二叉树，然后按照层级顺序连接起来。 6-3树和二叉树1的内容涵盖了树的基本概念、存储结构实现，以及如何通过特定的算法将非二叉树结构转换为更易于处理的二叉树形式。这对于理解和设计基于树的数据结构和算法非常重要，特别是在计算机科学中，树和森林是数据结构库中的基础元素。