理解与实现：BP神经网络的训练算法

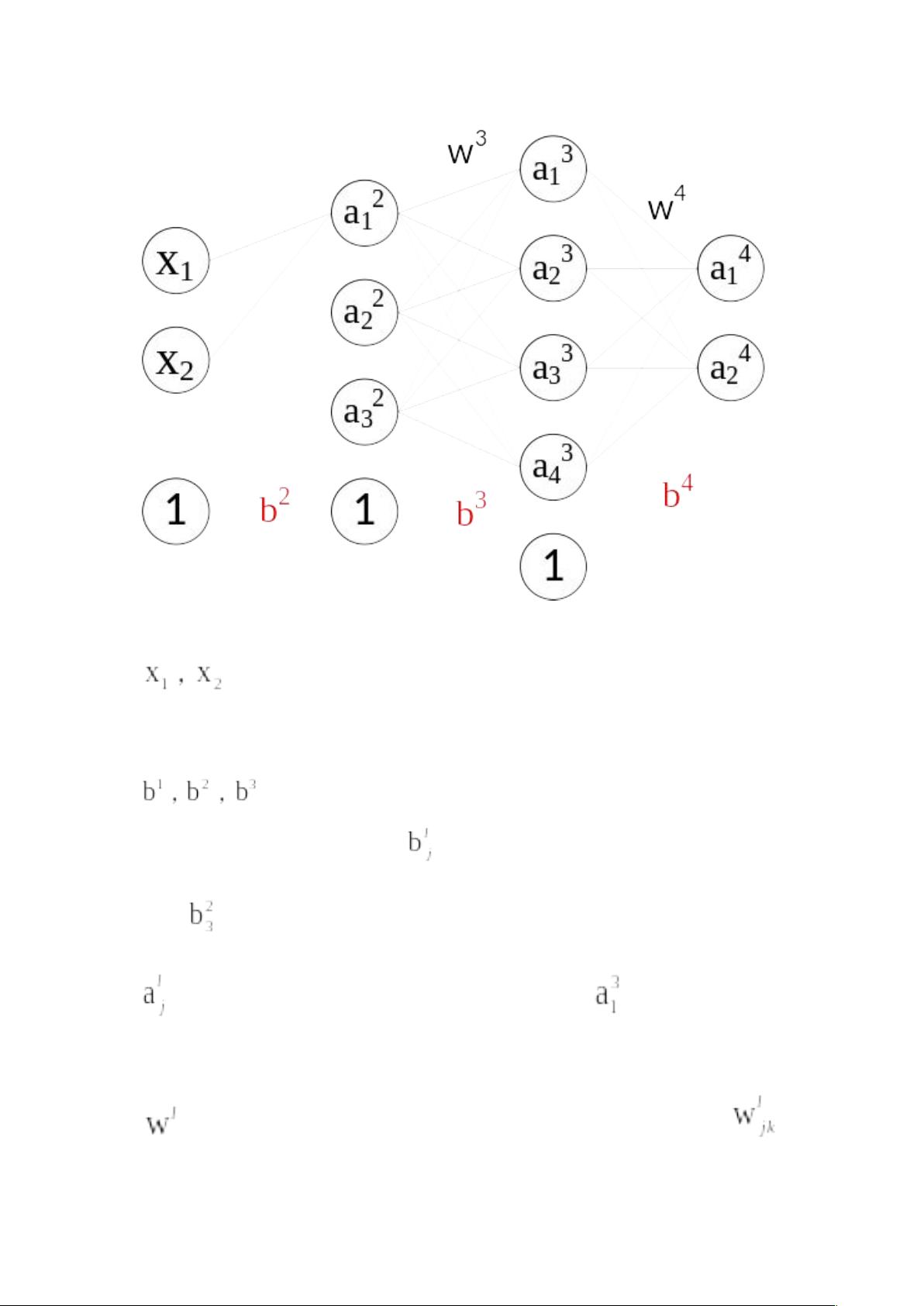
本文档详细介绍了BP神经网络的工作原理，包括网络结构、变量解释、代价函数的构建以及权值调整的最速下降法。通过理解这些概念，读者能够掌握BP神经网络的基本运作机制。 BP神经网络，全称为反向传播（Backpropagation）神经网络，是一种基于梯度下降优化算法的多层前馈神经网络。它主要用于非线性数据的分类和回归任务。在BP神经网络中，信息从输入层通过隐藏层向输出层单向传递，而错误信息则沿相反方向反向传播，从而调整网络的权重和偏置，实现网络的训练。 变量解释如下： 1. 输入向量 : 代表输入到神经网络的样本特征，本例中假设每个样本有两个特征。 2. 偏置 : 每个神经元都有自己的偏置，用 表示，例如 是第二层第三个神经元的偏置。 3. 权值 : 描述了神经元之间的连接强度， 是第l-1层第k个神经元到第l层第j个神经元的权值。 训练过程涉及的主要步骤： 1. 训练数据和验证集：网络训练需要一组已知输入和理想输出的训练样本。 2. 代价函数：定义为所有样本的均方误差，表示为 ，其中 是实际输出， 是期望输出， 是样本数量。 3. 权值更新：利用最速下降法（负梯度下降法），目标是降低代价函数。权值调整量由代价函数关于权值的偏导数决定。 4. 反传误差 : 是传播回前一层的误差，它简化了权值更新的计算，具有链式规则的性质，使得误差从输出层向输入层逐层反向传播。 公式推导： - 输出层的权值和偏置调整公式首先被计算，然后逐步向前层传播。 - 反传误差 : 定义为当前层神经元输出与期望输出之差乘以前一层的反传误差和权值。 - 权值更新公式 : 采用梯度下降法，更新权重为原权重加上学习率乘以偏导数（负梯度），其中 是学习率， 是当前样本的权值调整， 是所有样本的平均权值调整。 在实际应用中，由于计算量大，通常不是对所有样本都进行更新，而是采用部分样本（mini-batch）进行更新，这被称为小批量梯度下降。学习率 是一个超参数，控制权重更新的速度。当网络训练过程中误差下降缓慢，可能需要减小学习率以获得更好的收敛性能。 总结，BP神经网络通过反向传播误差来调整权重和偏置，以最小化网络输出与期望输出的差距。理解和掌握这些核心概念是构建和优化BP神经网络的基础。