随机信号处理：功率谱估计与MSE-SNR关系可视化及维纳滤波验证

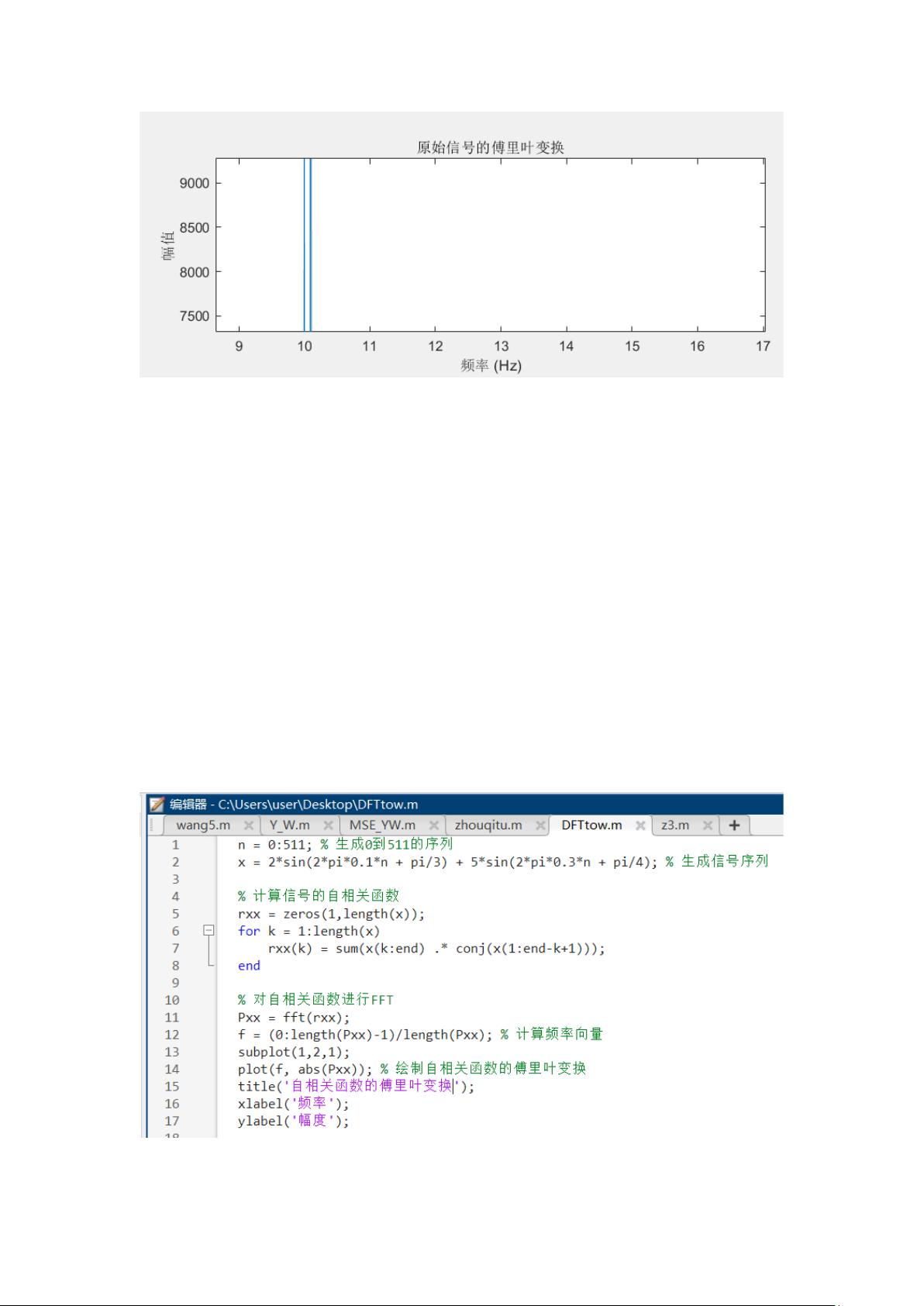
本实验报告主要探讨的是随机信号处理中的关键概念，包括功率谱估计和信号均方误差（MSE）与信噪比（SNR）的关系。实验的核心内容围绕着经典的信号处理方法，如经典傅立叶变换（Discrete Fourier Transform, DFT）、Yule-Walker方法、Laplace-Domain递推以及Burg算法在信号分析中的应用。 首先，实验目的是利用DFT来实现信号的频域分析，通过给定的信号（包含两个正弦波分量，其频率和幅值可调整），计算信号的离散傅里叶变换（DFT）。具体步骤包括： 1. **信号构建**：通过定义参数如采样点数N、采样时间序列n、采样频率fs等，创建包含两个正弦波的信号x，其中f1 = 0.1 Hz 和 f2 = 0.3 Hz。 2. **DFT与噪声处理**：使用MATLAB的fft函数计算信号的DFT，随后向信号中添加高斯白噪声，设定信噪比为10 dB。接着，应用低通滤波器以去除高频噪声，截止频率设为40 Hz，阶数为8。 3. **功率谱估计**：对滤波后的信号进行傅里叶变换，寻找滤波后信号的峰值，通常通过findpeaks函数获取。由于实际信号可能包含两个显著频率成分，实验着重于找到前两个最高峰值对应的频率值。 4. **MSE与SNR关系**：在噪声处理过程中，实验者会观察信号的均方误差（MSE）如何随着信噪比（SNR）的变化而变化，这有助于理解噪声对信号质量的影响。 5. **维纳欣钦定理验证**：实验还涉及到维纳-辛钦定理的应用，该理论在随机信号处理中十分重要，它描述了噪声对信号估计误差的期望行为。 报告中还提供了实际代码片段，展示了如何操作MATLAB实现这些步骤，并给出了估计的频率值，如f1估计值为0.101 Hz 和 f2估计值为0.301 Hz。此外，报告可能还包含不同信噪比条件下MSE变化的图形展示，以直观地呈现信号质量与SNR的关系。 本实验深入探究了随机信号处理技术在实际信号分析中的应用，涵盖了从信号建模、噪声处理到频谱估计及性能评估的关键环节，对于理解和掌握信号处理理论及实践具有重要价值。