动态规划解多段图最短路径：经典算法详解与C++实现

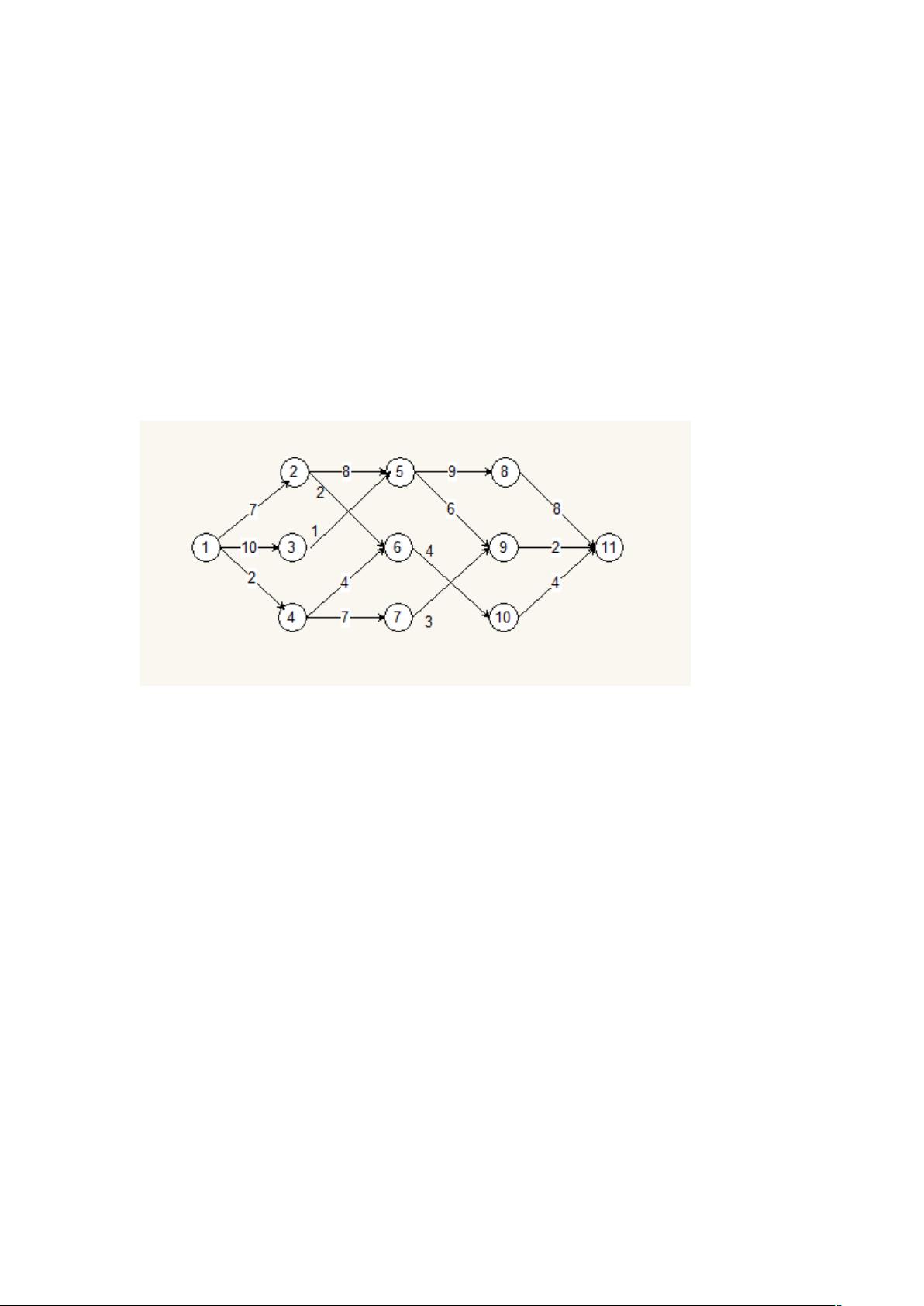
经典算法之多段图算法是一种用于解决图论问题的有效方法，特别适用于寻找多个源点到多个目标点之间的最短路径。在给定的问题中，我们关注的是计算节点1到节点11之间的最短路径，其中边的权重由箭头上的数字表示，代表从一个节点到另一个节点的距离。 算法的核心思想是利用动态规划来递归地更新每个节点到源点的最短距离。首先，算法从起点开始，逐步扩展至整个图。在每一层中，会遍历所有可能的前驱节点，检查是否有更短的路径。如果有，就更新当前节点的最短距离，并记录下到达这个最短路径的前驱节点。这样做的目的是为了构建一个从源点到各节点的最短路径树。 在代码实现上，采用二维数组`mix[i][j]`来表示从节点i到节点j的路径是否存在及其距离，如果不存在则表示为0。`out()`函数是一个关键部分，它负责计算每个节点到源点的最短距离。函数通过循环遍历所有节点，不断寻找更短路径，直至所有节点的距离都被更新。最后，`main()`函数初始化了边的权重矩阵，并调用`out()`函数输出结果。 整个算法流程包括以下几个步骤： 1. 初始化：定义一个二维数组表示图的结构，设置一个长度为节点数量的数组`len`来存储每个节点到源点的最短距离。 2. 动态规划：从源节点开始，依次更新其他节点的最短路径。对于每个节点，找出所有前驱节点中可以到达的最短路径，并更新其距离。 3. 重复计算：对图中所有节点进行同样的处理，直到所有节点的距离都被计算出来。 4. 逆向查找：在计算完成后，通过记录的前驱节点，回溯找到从源点到各个目标点的最短路径。 总结来说，经典算法之多段图算法利用动态规划的思想，结合具体的图结构和权重信息，有效地求解了多源点到多目标点的最短路径问题。这个算法在实际应用中，如网络路由、物流优化等领域都有广泛的应用。理解并掌握这个算法，对于深入理解图论和优化算法具有重要意义。