定点运算深入解析：补码加减法与运算器设计

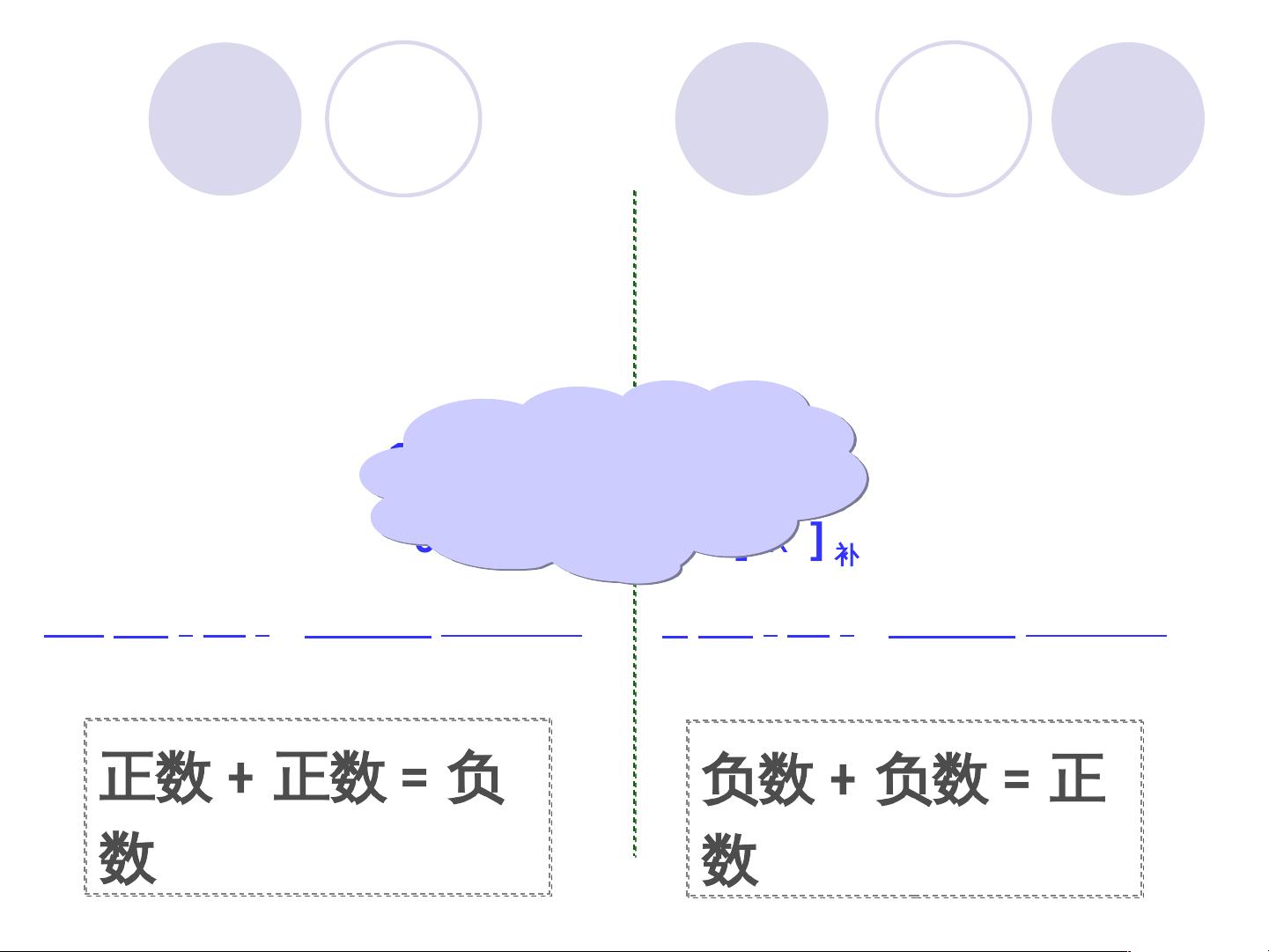
"组成原理课件，包括定点加减法、乘除法运算，以及运算器的组成等内容，旨在帮助学习者掌握计算机组成原理的基础知识。" 计算机组成原理是计算机科学与技术领域的重要基础课程，主要研究计算机硬件系统各组成部分的工作原理、设计方法以及它们之间的相互关系。本课件详细讲解了定点数的运算方法，这对于理解和设计计算机的运算器至关重要。 首先，课件介绍了定点加法和减法运算。在补码表示法中，定点数的加法和减法可以通过简单的位操作来实现。补码加法的基本公式是[x+y]补=[x]补+[y]补（对于模2^n+1的整数）或[x+y]补=[x]补+[y]补（对于模2的小数）。例如，正数相加时，两个数的补码直接相加；正数和负数相加时，需要将负数转换为其补码形式再进行加法运算。减法则可以看作是加法的特殊形式，即[x-y]补=[x]补+[-y]补，其中[-y]补是[y]补的反码加1。 课件还涵盖了定点乘法和除法运算的理解，虽然没有详细展开，但通常涉及移位和加法（乘法）或减法（除法）的组合。理解这些运算对于理解计算机中的算术逻辑单元（ALU）设计非常关键。 定点运算器的组成部分包括加法器、减法器、乘法器等，它们共同实现了各种算术和逻辑运算。学习者需要理解每个组件的功能以及如何通过这些组件设计出完整的运算器。 此外，课件强调了溢出判断方法，溢出发生在运算结果超出数据类型能表示的范围时。对于定点数，可以通过检查运算结果的符号位是否与预期相符来检测溢出。例如，在两个正数相加后得到负数，或者两个负数相加后得到正数，就可能存在溢出。 最后，浮点数的加减运算虽然未在此处详细阐述，但通常涉及到阶码的对齐和尾数的运算，这需要更高级的处理，比如对阶、规格化和舍入策略。 通过学习这个课件，学生不仅能掌握定点运算的细节，还能深入理解运算器设计的基本原理，为进一步学习计算机系统架构和高级硬件设计奠定坚实基础。