线性时不变系统的时间域分析与微分方程

"该资源是关于信号与系统的教学课件，主要探讨了连续系统的时域分析，特别是针对弱电领域的理论。内容涵盖了连续系统微分方程的特点、系统响应的分解形式、阶跃响应与冲激响应以及卷积的应用。通过实例分析了线性时不变（LTI）系统的微分方程，讲解了如何基于基尔霍夫电流定律（KCL）、基尔霍夫电压定律（KVL）和欧姆定律建立电学系统的微分方程，并涉及了二阶系统的表达式。" 在信号与系统的学习中，连续系统的时域分析是至关重要的一个部分。这一领域主要关注如何通过常系数线性微分方程来描述线性时不变系统的输入-输出特性。时域分析是一种研究输入信号经过系统处理后响应变化规律的方法，对于理解和设计电子系统具有基础性的作用。 首先，连续系统微分方程的特点在于它们是常系数线性微分方程。这些方程能够准确地表示系统动态行为，比如电容和电感元件组成的电路系统。例如，对于RC电路，根据基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL），可以得出微分方程，从而得到电流和电压之间的关系。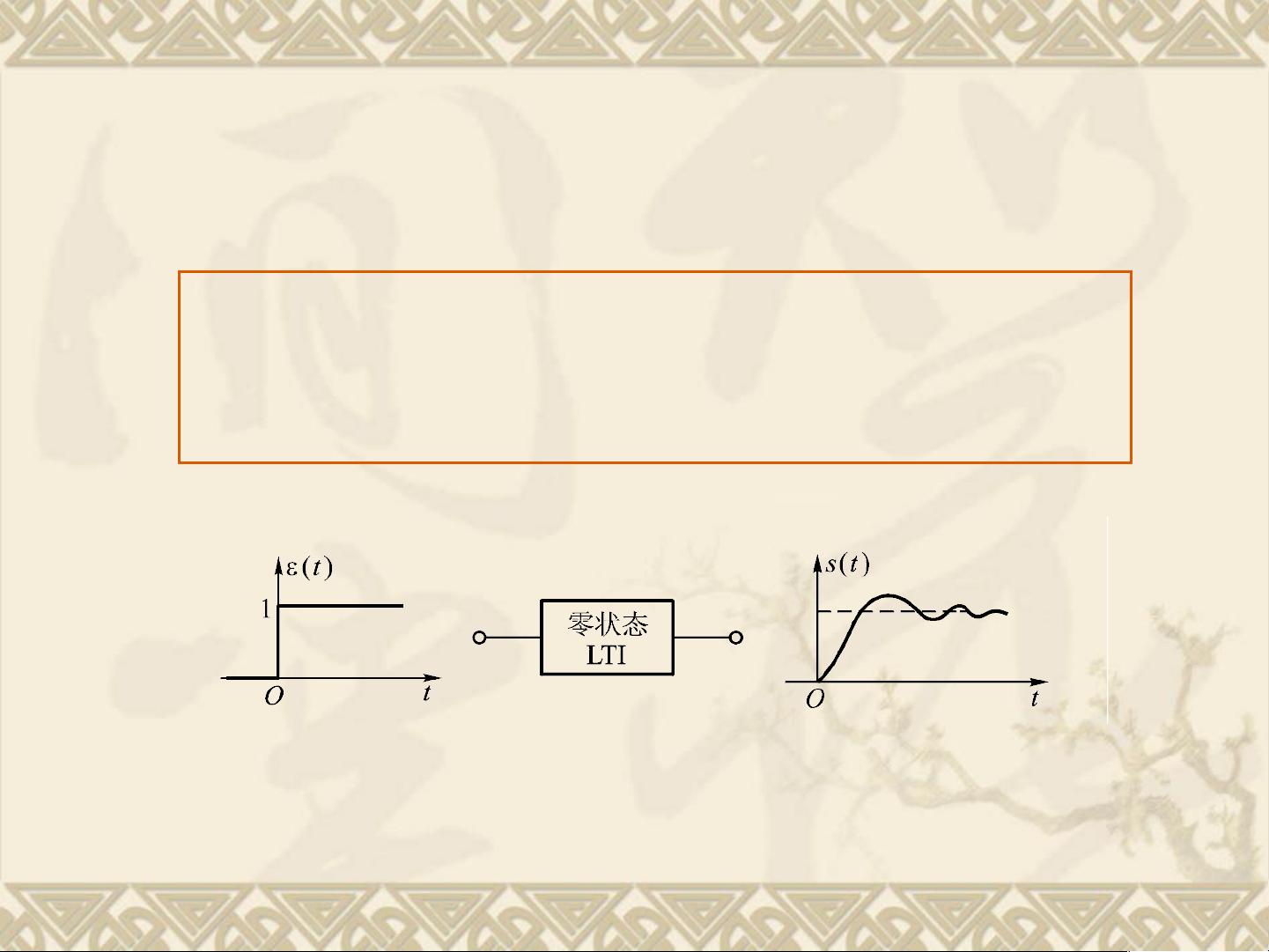 在分析系统响应时，通常会分解为阶跃响应和冲激响应两部分。阶跃响应是指当系统受到单位阶跃输入信号时，系统输出随着时间的变化情况；而冲激响应则是系统对单位冲激函数输入的响应，它是系统特性的基本描述，可以反映系统对任意输入信号的响应。冲激响应和阶跃响应可以通过卷积运算得到其他形式的输入信号对应的系统响应。 卷积是连续系统时域分析中的核心工具，它在求解系统输出时起到关键作用。卷积运算可以将系统的冲激响应与输入信号相乘积分，得到系统的实际输出。这对于计算复杂输入信号下系统的响应非常有用，广泛应用于滤波器设计、信号处理等多个领域。 对于二阶系统，其微分方程通常包含两个二阶导数项，如LC串联或并联电路。这种类型的系统表现出更复杂的动态特性，包括过阻尼、欠阻尼和临界阻尼等不同响应类型，这在控制系统设计和稳定性分析中具有重要意义。 该资源深入浅出地介绍了连续系统的时域分析，通过具体的电路例子展示了如何建立微分方程，以及如何利用这些方程来分析系统响应。这对于理解和应用弱电领域的信号处理理论至关重要。