最小二乘算法分析与特点总结

该文档详细分析了多种最小二乘算法，包括RLS遗忘因子法、RFF遗忘因子递推算法、RFM限定记忆法、RCLS偏差补偿最小二乘法、增广最小二乘法、RGLS广义最小二乘法、RIV辅助变量法、Cor-ls相关最小二乘法（二步法）、MLS多级最小二乘法以及yule_walker辨识算法，并提供了每种算法的仿真思路、辨识结果及其特点。同时，文档还包含了这些算法的MATLAB程序实现。 一、RLS遗忘因子法 RLS（Recursive Least Squares）遗忘因子法是一种在线参数估计方法，通过遗忘因子β控制旧数据的影响。在仿真中，输入信号采用M序列，辨识模型为线性系统，加权阵Λ取为衰减因子β=0.98，数据长度为402。辨识结果与理论值相符，表明该方法能够有效地处理动态变化的数据。 二、RFF遗忘因子递推算法 RFF（Recursive Forgetting Factor）算法在RLS基础上进行了优化，适用于快速变化的环境。其特点在于更灵活地调整遗忘因子以适应系统的实时变化。 三、RFM限定记忆法 RFM（Restricted Memory）算法限制了存储的历史数据量，以平衡计算复杂性和精度。通过控制记忆大小，可以在有限的计算资源下获得良好的估计性能。 四、RCLS偏差补偿最小二乘法 RCLS（Recursive Compensated Least Squares）考虑了系统偏差，通过偏差补偿来提高估计的准确性。在辨识过程中，它能有效地减少由于系统非线性或模型误差导致的偏差。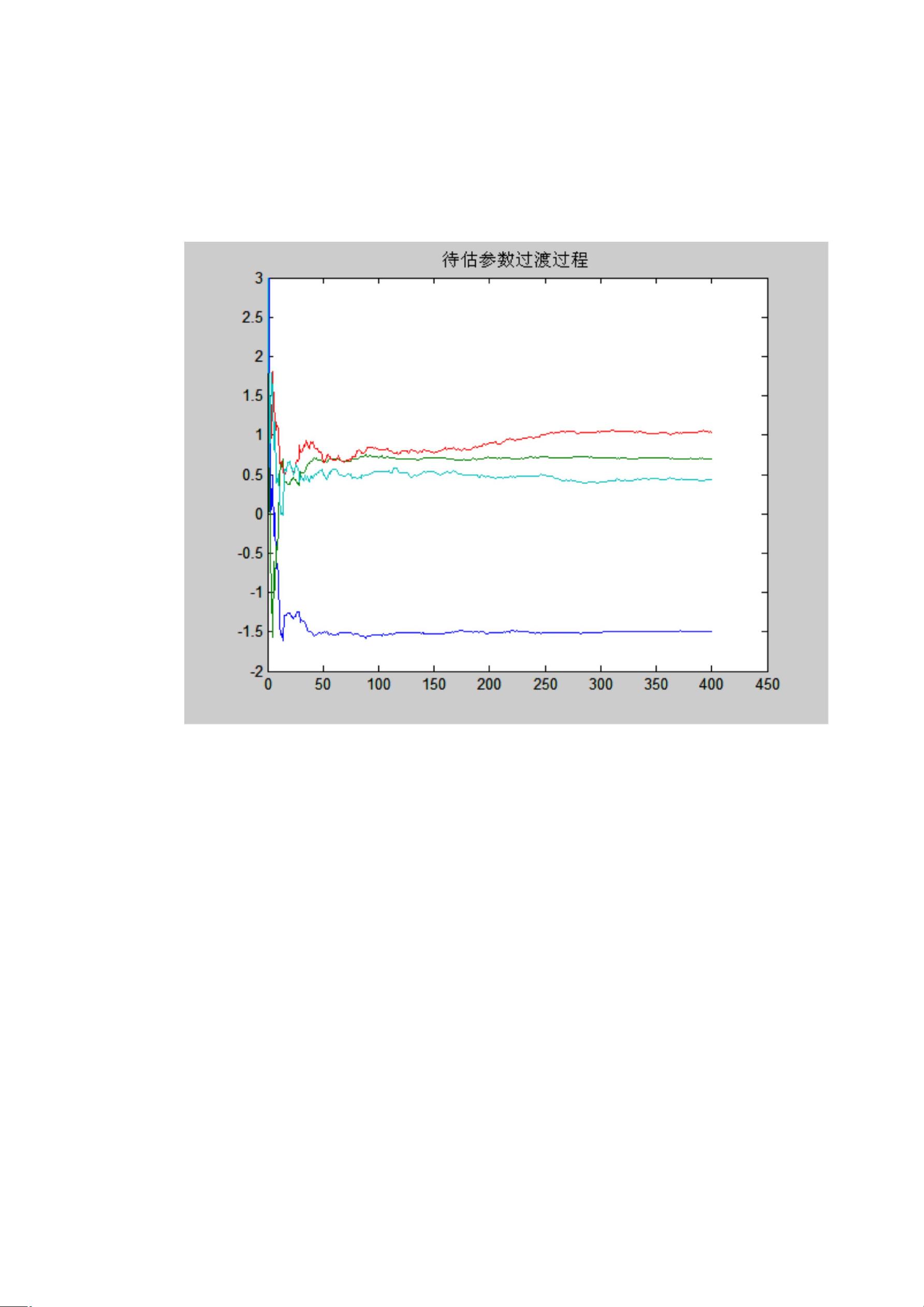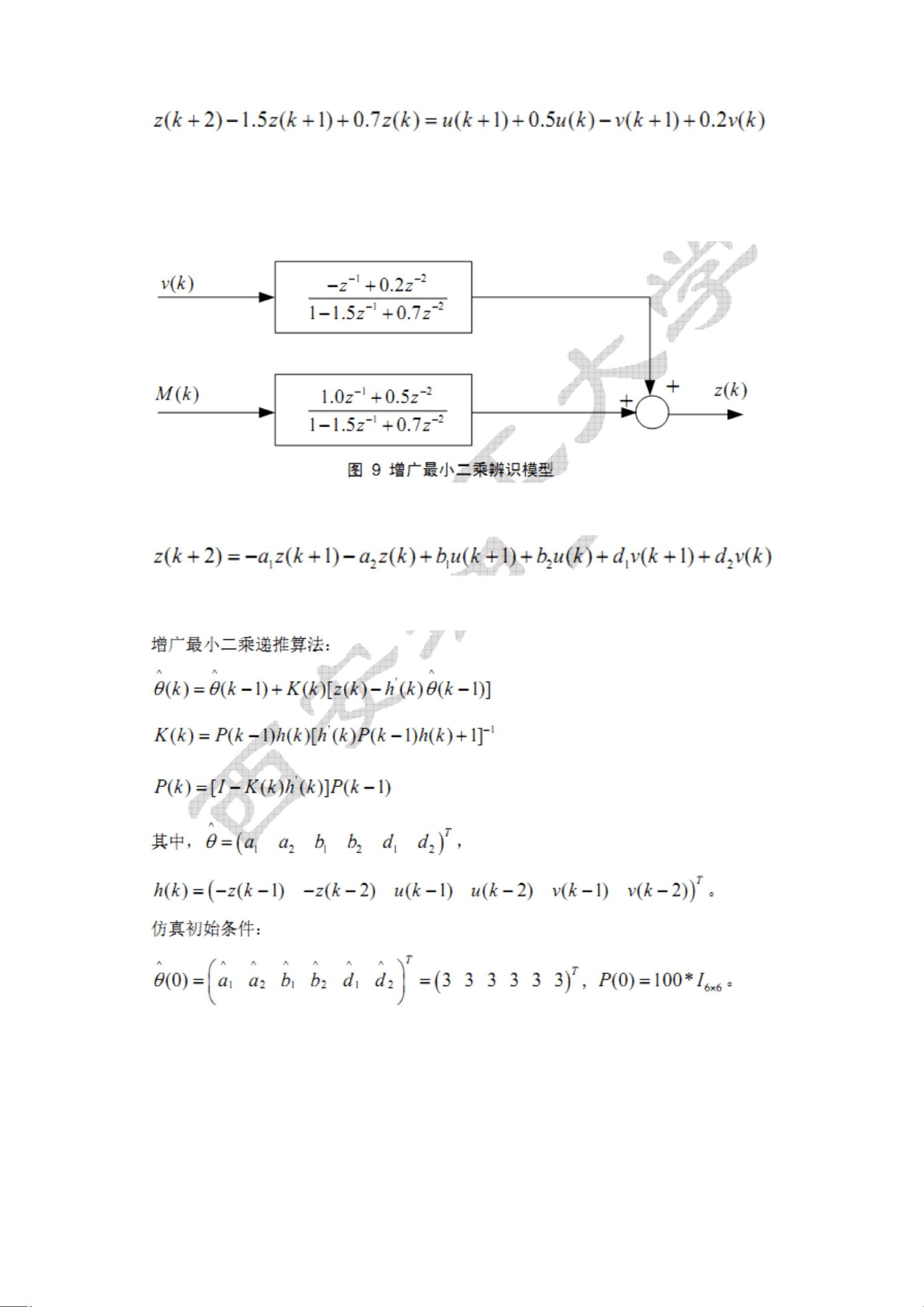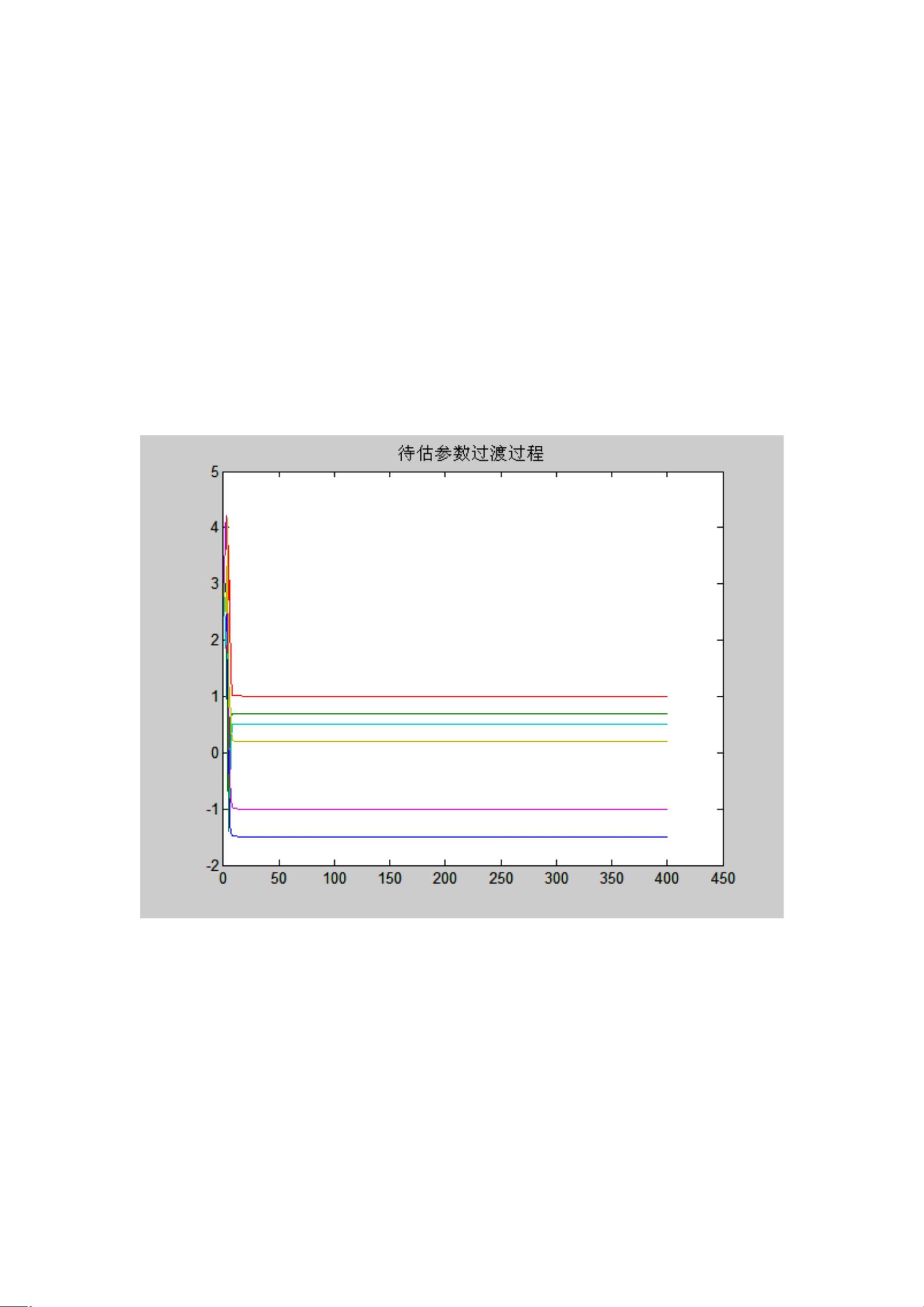 五、增广最小二乘法 RELS（Recursive Augmented Least Squares）算法扩展了系统模型，将模型误差纳入考虑，提高了辨识的鲁棒性。在仿真中，它能够处理包含不确定性和噪声的数据。 六、RGLS广义最小二乘法 RGLS（Recursive Generalized Least Squares）适用于带有协方差矩阵的观测数据，通过对观测数据进行加权处理，提高了对噪声的抑制能力。 七、RIV辅助变量法 RIV（Regression with Interpolating Variables）利用辅助变量来改善模型的拟合度，特别适用于非线性系统的辨识。 八、Cor-ls相关最小二乘法（二步法） Cor-ls（Correlated Least Squares）算法分为两步进行，首先估计协方差，然后进行最小二乘解算，适用于处理相关观测数据的情况。 九、MLS多级最小二乘法 MLS（Multi-Level Least Squares）通过分层次的辨识策略，逐步细化模型，适合处理多层次的复杂系统。 十、yule_walker辨识算法 Yule-Walker算法是AR（Auto-Regressive）模型辨识的经典方法，通过自回归系数估计模型参数，适用于时间序列分析。 这些算法在MATLAB中的实现为实际应用提供了参考，可以根据不同的系统特性和需求选择合适的最小二乘算法。通过理解和掌握这些算法，可以有效地进行系统辨识和参数估计。