概率统计公式精要:从基础到正态分布
需积分: 50 159 浏览量
更新于2024-08-01
1
收藏 506KB DOC 举报
"这篇资料汇总了日常常用的概率公式,涵盖了概率、方差、协方差、标准差、期望以及正态分布等核心概念,适用于数据分析、统计学学习和相关IT应用。"
在概率论和统计学中,这些基本概念扮演着至关重要的角色。让我们逐一深入探讨:
1. **概率**:概率是描述一个事件发生的可能性,范围在0到1之间,1表示必然发生,0表示不可能发生。等可能性事件的概率通常基于事件的数量和总可能事件的数量。
2. **互斥事件**:互斥事件是指不能同时发生的事件,如抛一枚硬币,正面朝上和反面朝上是互斥的。两个互斥事件A和B的发生概率是它们各自概率的和。
3. **独立事件**:独立事件是指一个事件的发生不会影响另一个事件发生的概率。两个独立事件A和B同时发生的概率是它们各自概率的乘积。
4. **n次独立重复试验**:伯努利试验中,某事件恰好发生k次的概率由二项式分布给出,公式为C(n, k) * p^k * (1-p)^(n-k),其中p是单次试验中事件发生的概率。
5. **离散型随机变量的分布列**:离散型随机变量的每一个可能值及其对应的概率构成分布列,其概率和为1,期望值等于每个值乘以其对应概率的和。
6. **数学期望**(均值):期望是随机变量的平均值,反映了随机变量取值的集中趋势。对于离散型随机变量X,其期望E(X) = Σ[xi * P(xi)]。
7. **方差**:方差衡量随机变量或一组数据的离散程度,定义为各个值与期望的差的平方的期望值,记作Var(X)。方差越大,数据的波动性越大。
8. **标准差**:标准差是方差的算术平方根,标准差σ提供了关于数据分布的直观感觉,它同样反映了数据的分散程度。
9. **正态分布**:正态分布是一种连续型概率分布,具有钟形曲线,其中μ是平均值,σ是标准差。正态分布广泛应用于自然科学和社会科学领域,例如人口身高分布。
10. **协方差**:协方差用于度量两个随机变量之间的线性相关性,正值表示正相关,负值表示负相关,0表示独立。
11. **相关系数**:相关系数r是协方差和两个变量标准差的商,范围在-1到1之间,|r|越接近1表示相关性越强,接近0表示相关性弱。
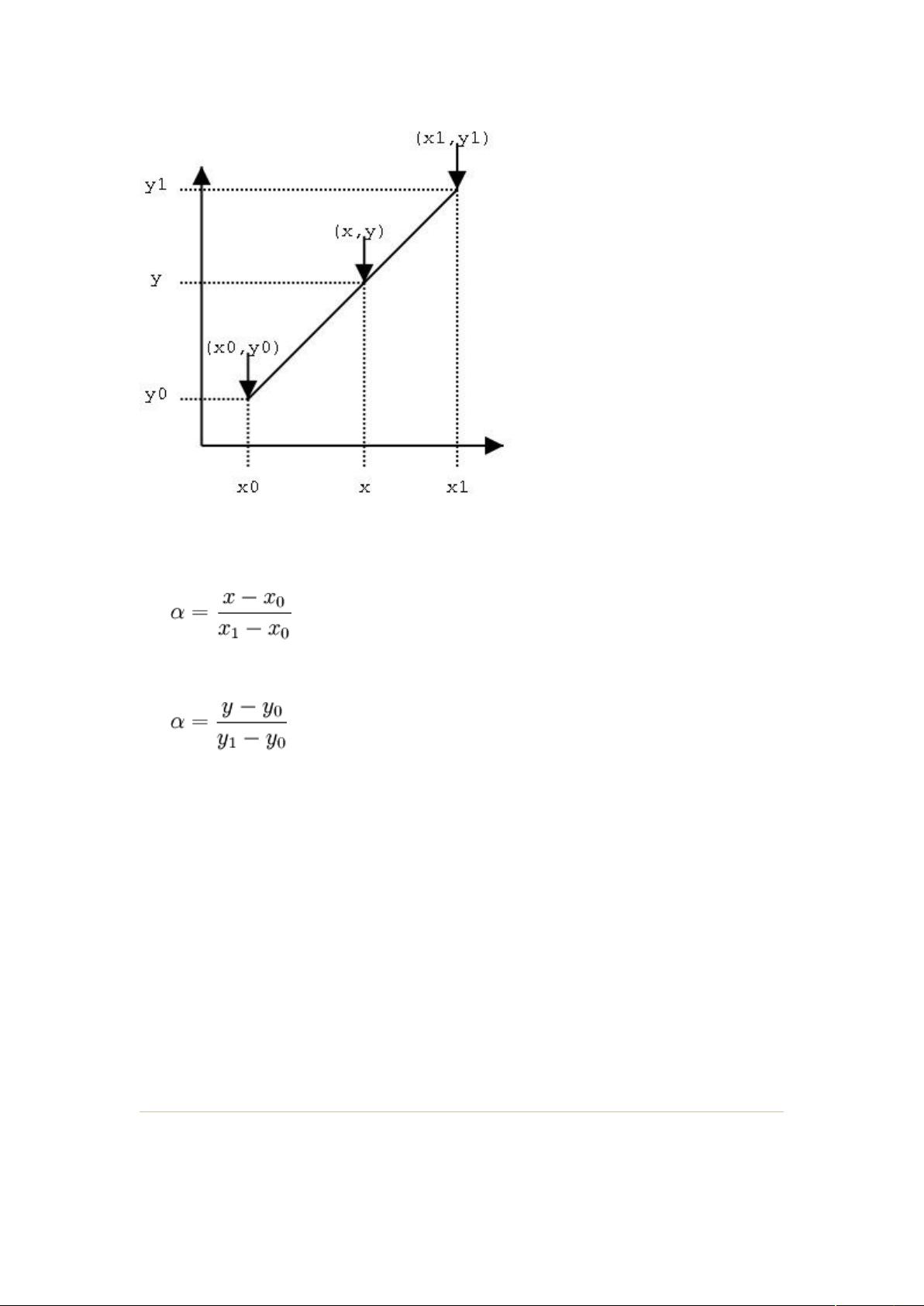
12. **回归直线方程**:在统计学中,回归分析用来预测一个变量如何依赖于另一个变量,其方程形式为y = ax + b,其中a是斜率,b是截距,表示当x=0时y的值。
13. **相关系数的性质**:相关系数的绝对值大小表示了两个变量的相关程度,而符号决定了这种相关是正向还是负向。
这些公式在数据分析、机器学习、风险评估以及预测模型构建等多个IT领域都有广泛应用。理解并熟练运用这些基础概率公式,有助于解决实际问题,提升分析和决策能力。
118 浏览量
点击了解资源详情
654 浏览量
2022-07-12 上传
119 浏览量
129 浏览量
303 浏览量
2024-11-25 上传
503 浏览量
lanxiao9812
- 粉丝: 1
最新资源
- C语言实现LED灯控制的源码教程及使用说明
- zxingdemo实现高效条形码扫描技术解析
- Android项目实践:RecyclerView与Grid View的高效布局
- .NET分层架构的优势与实战应用
- Unity中实现百度人脸识别登录教程
- 解决ListView和ViewPager及TabHost的触摸冲突
- 轻松实现ASP购物车功能的源码及数据库下载
- 电脑刷新慢的快速解决方法
- Condor Framework: 构建高性能Node.js GRPC服务的Alpha框架
- 社交媒体图像中的抗议与暴力检测模型实现
- Android Support Library v4 安装与配置教程
- Android中文API合集——中文翻译组出品
- 暗组计算机远程管理软件V1.0 - 远程控制与管理工具
- NVIDIA GPU深度学习环境搭建全攻略
- 丰富的人物行走动画素材库
- 高效汉字拼音转换工具TinyPinYin_v2.0.3发布