"基于分数阶微积分的Buck电路建模与PID控制研究"
版权申诉
65 浏览量
更新于2024-02-20
1
收藏 2.23MB DOCX 举报
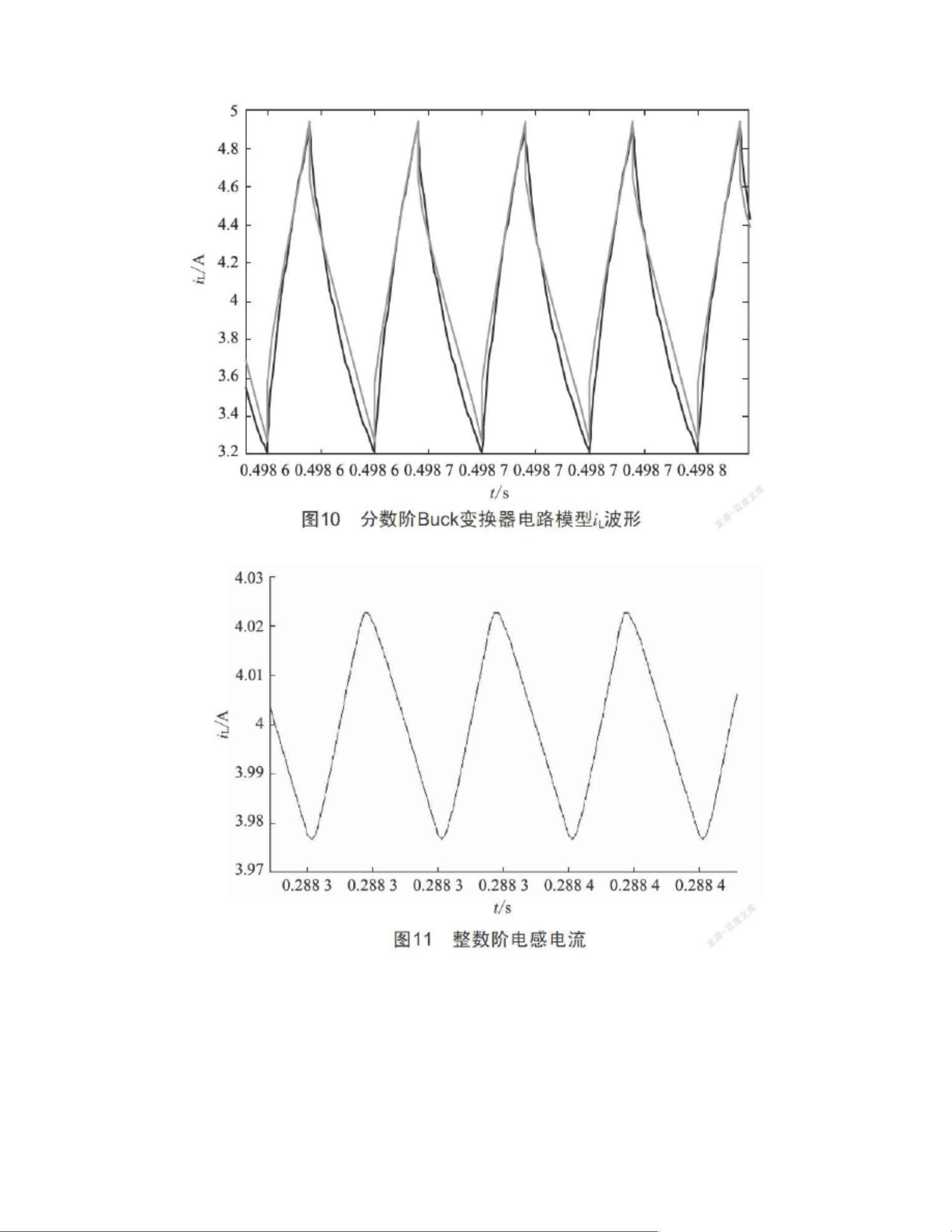
本文基于分数阶微积分理论和实际电路中电感与电容呈现分数阶特性的事实,研究了分数阶Buck电路的建模和控制方法。首先运用状态空间平均法建立了在电感电流连续情况下的分数阶Buck电路的数学模型和电路模型,提出了分数阶Buck电路纹波分析与连续条件,并推导出了占空比至输出电压和输入电压至输出电压的传递函数。研究结果表明,该模型相对于整数阶模型更能精确反映实际电路工作状态。接下来,基于Matlab/Simulink软件对模型进行了仿真验证,验证了该模型的正确性。随后,基于ITAE最优控制方法设计了分数阶PID控制器对该模型进行控制,并对补偿后的传递函数进行了仿真,验证了该控制器的有效性。本研究的关键词包括分数阶微积分、Buck变换器、建模和分数阶PID控制。
自Leibniz在1695年首次提出关于将微分阶次推广到非整数阶的问题以来,分数阶微积分学说经过300多年的发展,在1960年开始逐步推广到科学与工程领域。意大利学者Caputo与Mainardi教授为基于分数阶导数建立的耗散波动方程提出了重要的理论基础,为分数阶微积分的应用奠定了基础。本文针对分数阶微积分理论在电路中的应用进行了深入研究,通过建立分数阶Buck电路的数学模型和电路模型,验证了分数阶模型能更准确地反映实际工作状态。通过仿真验证和分数阶PID控制器的设计,验证了该控制器对电路的有效控制,为分数阶微积分在电路领域的应用提供了重要的理论和技术支持。
在研究中发现,分数阶微积分在电路建模和控制中具有很大的潜力和优势,能够更准确地描述电路的非线性特性和动态特性。分数阶Buck电路的建模和控制研究为分数阶微积分的应用提供了一个具体的场景,并为分数阶微积分在电路领域的进一步应用奠定了基础。随着电路技术的不断发展和电子设备的不断升级,分数阶微积分的应用将会越来越广泛,为电路领域的研究和发展带来新的机遇和挑战。
总的来说,本文通过对分数阶Buck电路的建模和控制研究,验证了分数阶微积分在电路领域的应用潜力,为分数阶微积分在工程技术领域的应用提供了重要的理论和技术支持。未来的研究方向可以继续深入探讨分数阶微积分在更多电路场景中的应用,为工程技术领域的发展做出更多的贡献。
点击了解资源详情
2022-11-19 上传
2022-11-18 上传
2022-11-24 上传
2022-11-18 上传
2022-11-13 上传
春哥111
- 粉丝: 1w+
最新资源
- Delphi纯源码QR二维码生成器支持中英文
- 罗克韦尔CENTERLINE 2500智能马达控制中心的特性与功能
- ARIMA模型预测股票价格准确性分析与未来工作展望
- ECharts图表应用与区间查询功能展示
- Java+EE技术面试题解析与源码工具应用
- 探索SVG在WebGIS开发中的应用与源码解析
- JAVA常用算法项目:LeetCode分类刷题指南
- Desech Studio中Angular插件的使用与测试教程
- 51单片机走马灯效果的Proteus仿真教程
- JavaScript塔围攻1第32章核心解析
- 罗克韦尔可视化解决方案选型指南全面解析
- LeetCode刷题指南:按语言分类的编程题库
- Kali Linux环境下WiFi攻击与防护技术分析
- pickadate.js-gh-pages压缩包使用教程
- MV C++ 14.0新版本特性及功能介绍
- Bootstrap网页自定义选项查询字符串插件介绍