JavaScript图像处理：仿射变换详解

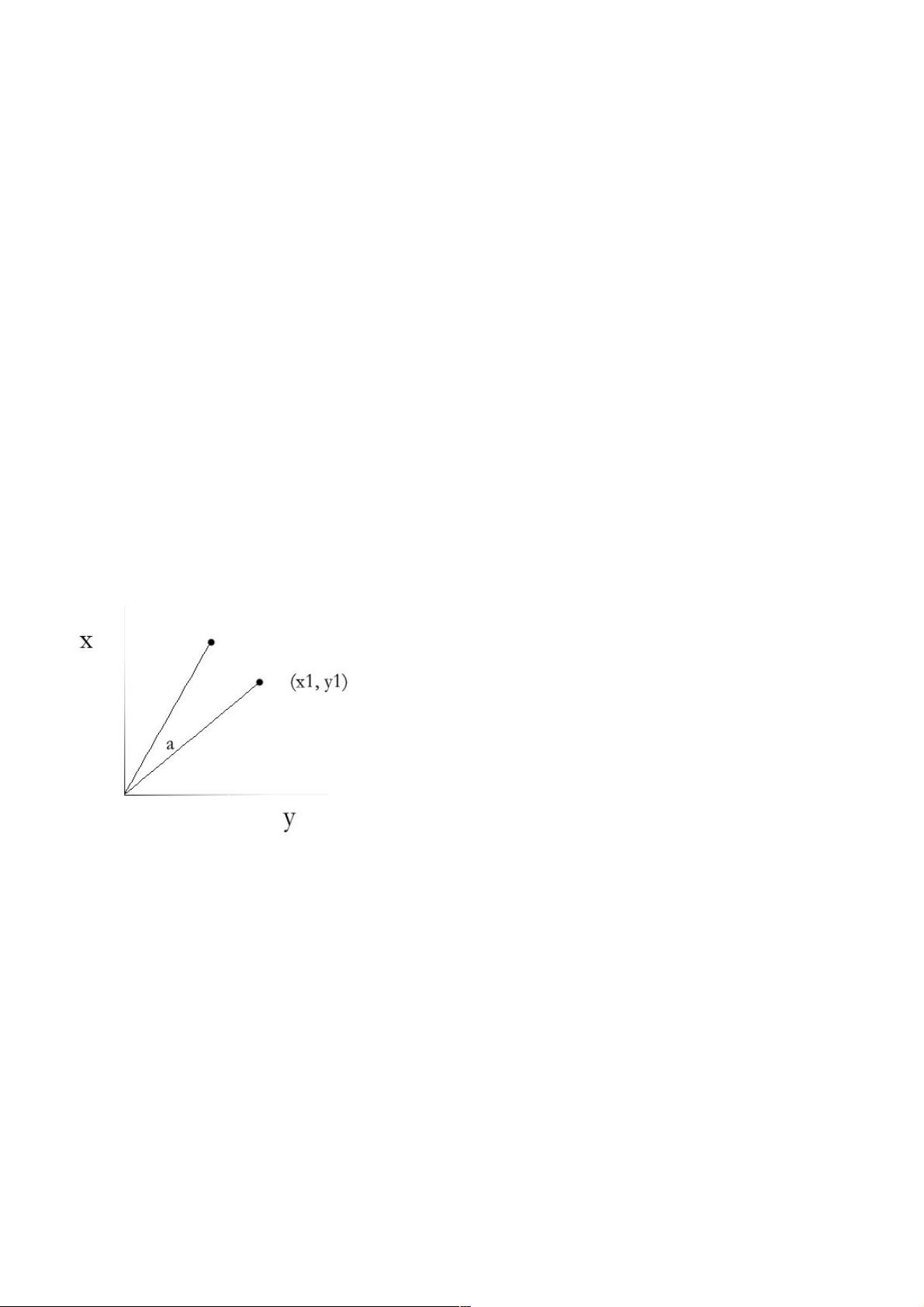
"本文深入探讨了JavaScript中的图像处理技术，特别是仿射变换的深度理解。通过数学解析，解释了如何进行图像的旋转和平移，并提供了获取旋转矩阵的函数实现及仿射变换的代码示例。" 仿射变换是图像处理中的重要概念，它涉及到图像的几何变形，包括缩放、旋转和平移等操作。在JavaScript中，可以利用矩阵运算来实现这些变换。任何仿射变换可以表示为一个线性变换（矩阵乘法）与一个平移变换（向量加法）的组合。线性变换通常用于处理图像的比例和旋转，而平移变换则负责移动图像的位置。 首先，我们来看一个简单的数学问题：如何将一个点(x1, y1)绕原点旋转a角度。在极坐标系统中，点(x1, y1)可表示为(r, β)，旋转后变为(r, α + β)。再转换回直角坐标，我们得到旋转后的点坐标为(cos(α + β) * r, sin(α + β) * r)。利用三角恒等式cos(α + β) = cosαcosβ - sinαsinβ和sin(α + β) = sinαcosβ + cosαsinβ，我们可以推导出点(x1, y1)旋转a角度后的坐标为(x1 * cosα - y1 * sinα, x1 * sinα + y1 * cosα)。 对于平移变换，只需将点的坐标加上一个平移向量(c, d)即可。在矩阵表示中，平移变换可以用一个2x3的矩阵B来描述，其中B的最后两列就是平移向量。 为了实际应用这些变换，我们需要创建一个表示旋转的矩阵。以下是一个JavaScript函数，用于根据给定的角度、x和y坐标生成2D旋转矩阵： ```javascript var getRotationArray2D = function(__angle, __x, __y) { var sin = Math.sin(__angle) || 0, cos = Math.cos(__angle) || 1, x = __x || 0, y = __y || 0; return [cos, -sin, -x, sin, cos, -y ]; }; ``` 该函数返回一个旋转矩阵，但请注意，这里的原点默认位于图像的左上角，这可能不适用于所有情况。 仿射变换的完整实现通常涉及一个更复杂的函数，如`warpAffine`，它接收源图像、旋转矩阵和目标图像作为参数。这个函数会实际执行仿射变换，将源图像变形为目标图像。这里省略了`warpAffine`函数的完整代码，但通常它会遍历源图像的每个像素，应用旋转矩阵，并将结果写入目标图像。 在JavaScript图像处理中，可以使用诸如HTML5 Canvas API或专门的图像处理库（如OpenCV.js）来执行这些仿射变换。这些工具提供了一种在Web环境中进行图像处理的强大方式，包括但不限于仿射变换。 总结来说，仿射变换是图像处理的关键技术，通过矩阵运算能够实现图像的旋转、缩放和平移。在JavaScript中，可以编写函数来生成旋转矩阵并应用仿射变换，从而在网页上实现动态的图像变形效果。理解这些概念和实现方法对于进行复杂的交互式图形设计和分析是非常重要的。