数字图像处理课件：傅立叶变换及频域图像增强

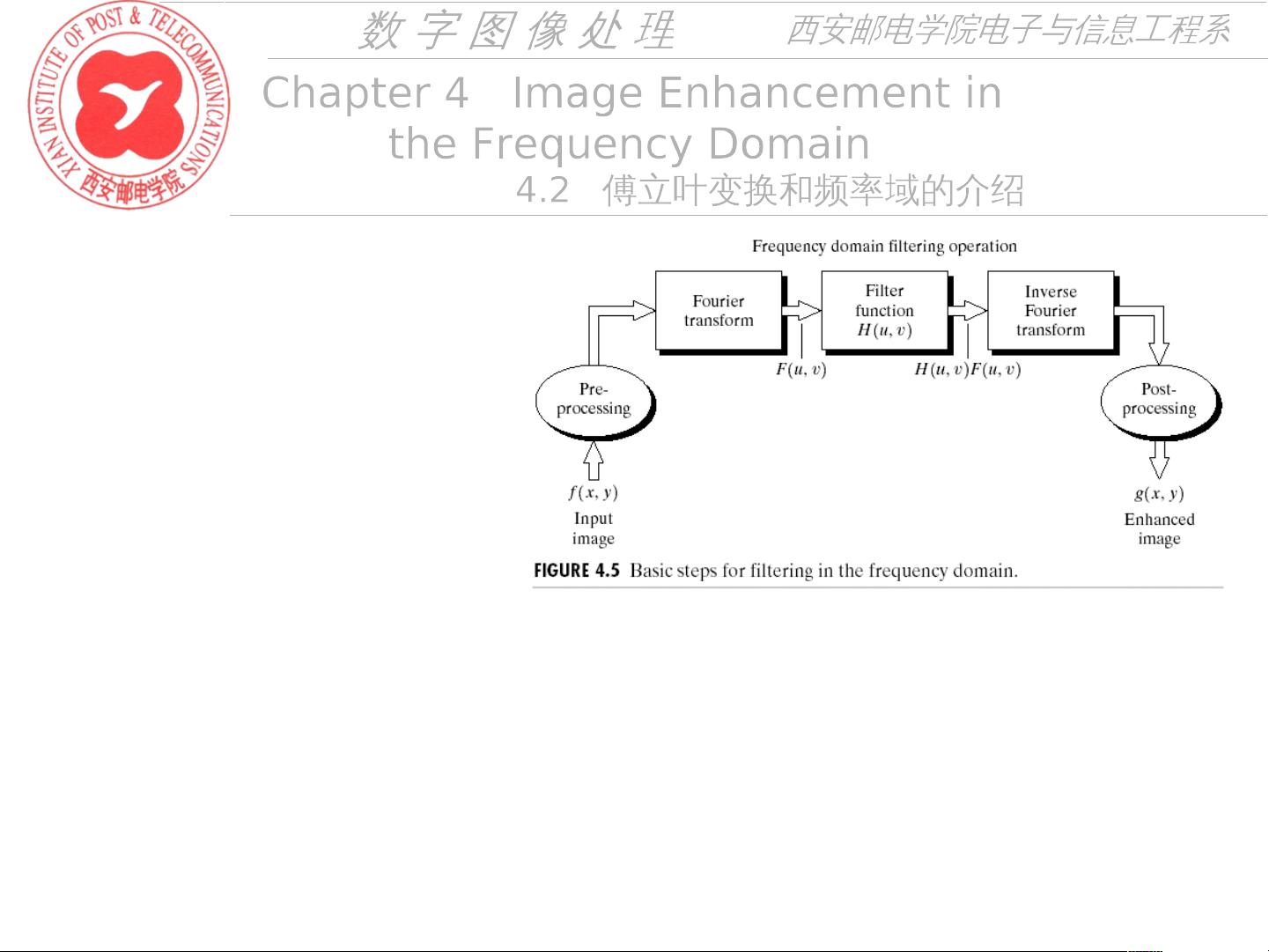
数字图像处理是对数字图像进行操作和改进的一门学科。本课件的第3、4、5章分别介绍了数字图像处理中的傅立叶变换以及其在图像增强中的应用。 傅立叶变换是由法国数学家傅立叶提出的一种数学方法，用于将一个函数表示为不同频率的正弦或余弦函数的和的形式。对于周期函数，傅立叶变换可以表示为傅立叶级数，而对于非周期函数，则可以用傅立叶变换表示为加权正弦和余弦函数的积分形式。 傅立叶变换在信号处理领域有着广泛的应用，特别是在数字计算和快速算法的发明中起到了重要作用。通过傅立叶变换，可以将信号从时域转换到频域，从而更加直观地观察信号的频率成分及其强弱。 在数字图像处理中，傅立叶变换同样起到了至关重要的作用。通过对图像进行傅立叶变换，我们可以将图像从空域转换到频域，从而实现图像增强的目的。在频域中，我们可以通过调整不同频率成分的幅度和相位来改善图像的质量。 在本章节中，我们首先介绍了一维傅立叶变换及其反变换的数学表达式，以及它们在频域中的几何表示。一维傅立叶变换可以将一个一维信号转换为频域中不同频率成分的复数表示。反变换则可以将频域表示的信号重新转换回空域表示。 接下来，我们介绍了二维傅立叶变换及其反变换的推导过程。二维傅立叶变换可以将一个二维图像转换为频域中不同频率成分的复数表示。通过调整不同频率成分的幅度和相位，我们可以对图像进行各种增强操作，如增加对比度、增强边缘等。 除了傅立叶变换的数学表达式和推导过程，本章节还介绍了傅立叶变换在图像增强中的具体应用。通过对频域图像进行滤波操作，我们可以实现图像的均衡化、锐化、平滑等增强效果。特别是在去除图像中的噪声时，频域滤波技术有着较好的效果。 本章还介绍了频域图像增强中的一些常见问题和挑战，如频域滤波器的设计、频域滤波引起的图像振铃效应等。通过了解这些问题，我们可以更好地理解频域图像增强的原理和方法，从而更好地应用于实际图像处理中。 总之，本章通过介绍傅立叶变换及其在频域图像增强中的应用，帮助我们更好地理解数字图像处理的基本原理和方法。通过掌握傅立叶变换的数学表达式和频域图像增强的相关技术，我们可以对数字图像进行更加灵活和精确的处理，提高图像的质量和清晰度。