非线性非平稳时间序列分析：Hilbert-Huang变换详解

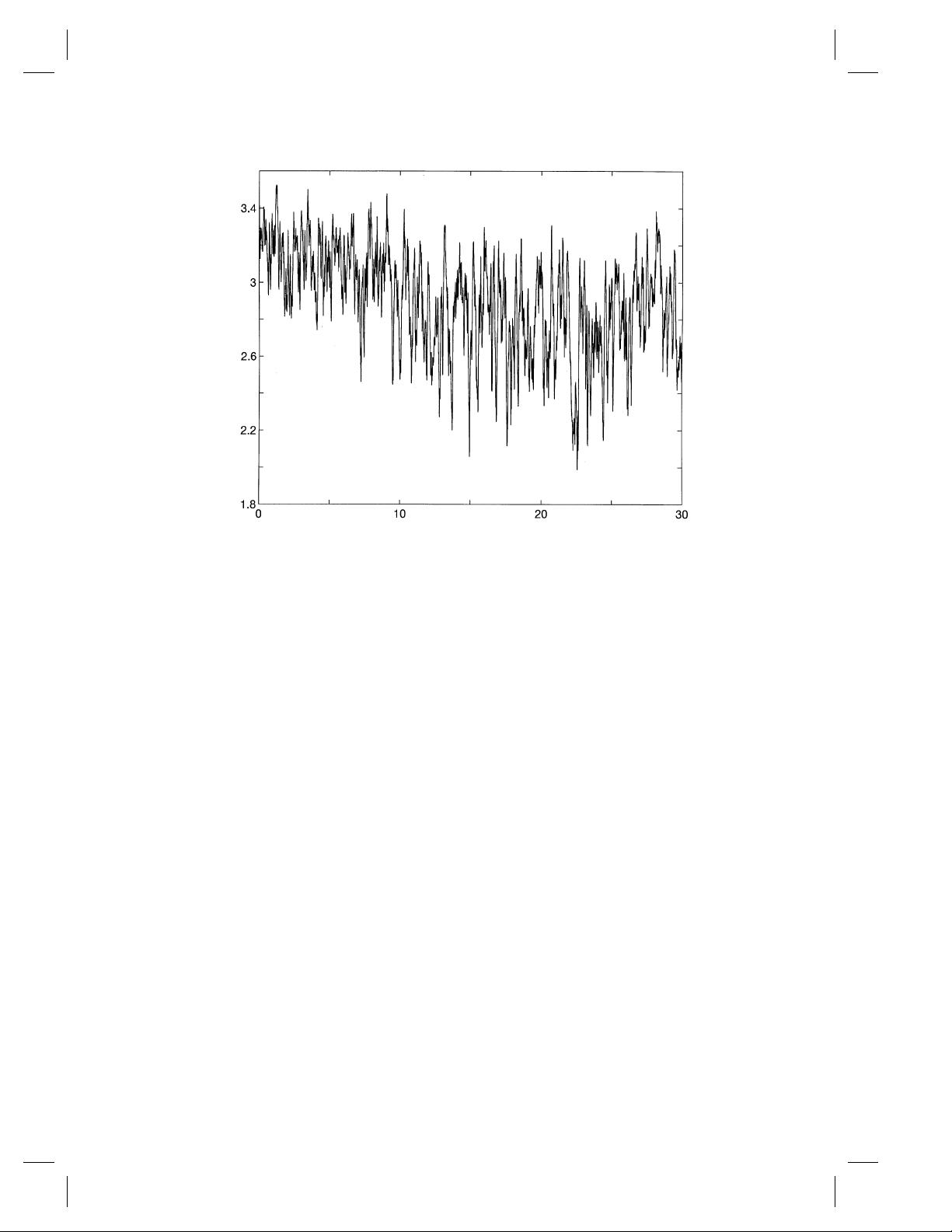
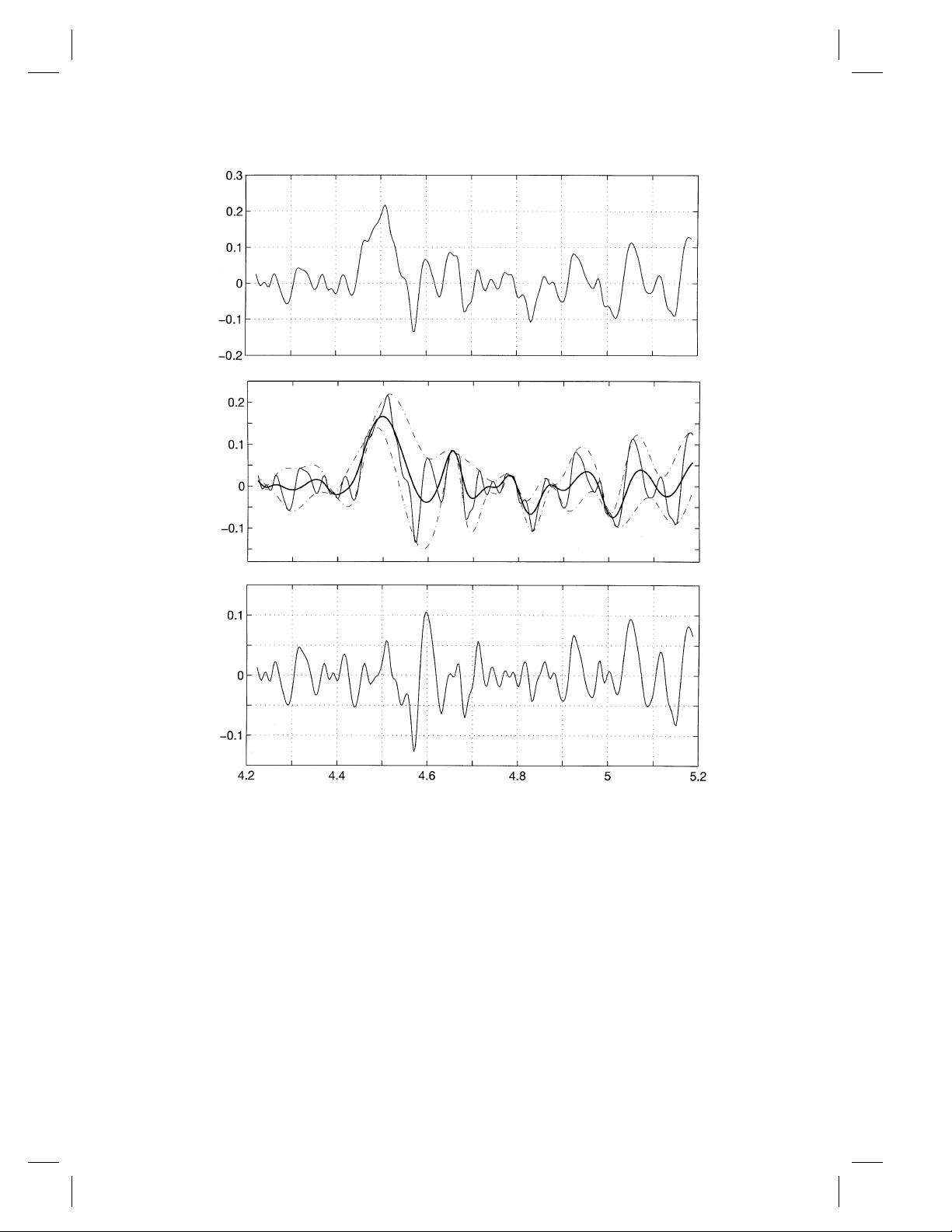
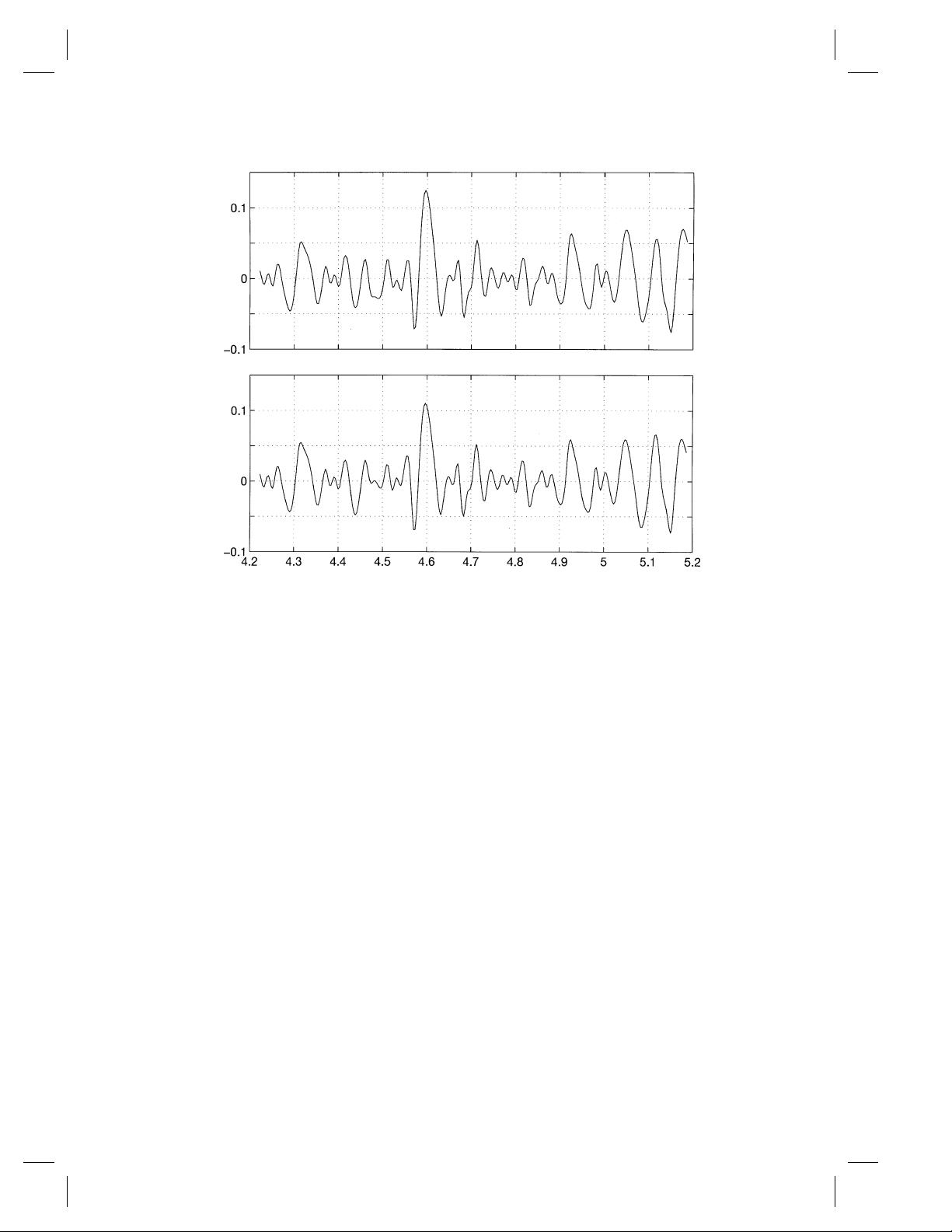
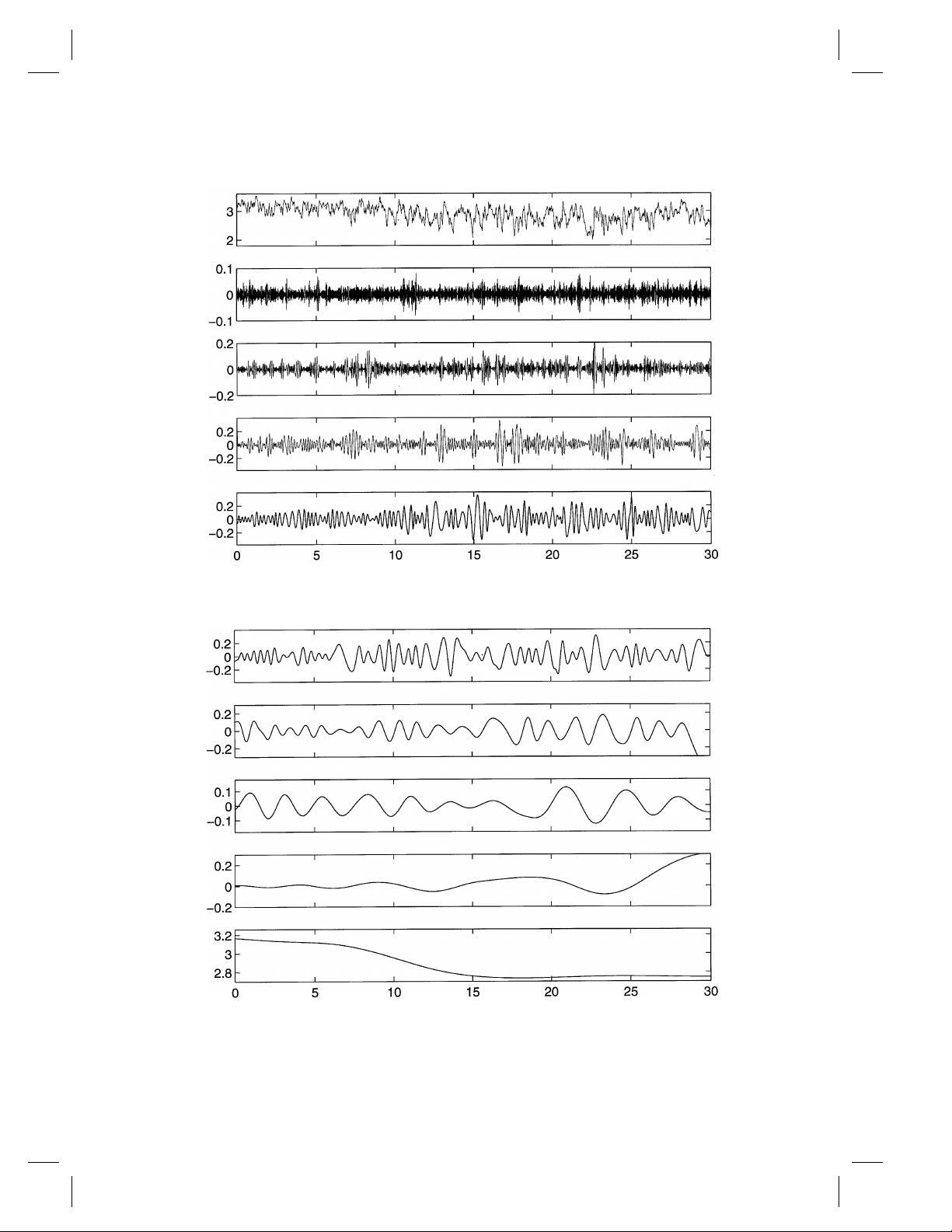
"Hilbert-Huang变换是一种用于非线性、非平稳时间序列分析的方法，由Norden E. Huang等人在1996年提出。它结合了经验模态分解（Empirical Mode Decomposition, EMD）和希尔伯特谱（Hilbert Spectrum），为复杂信号的分析提供了新的途径。该方法主要应用于地球科学、海洋学、大气科学、工程学等领域。" 正文： Hilbert-Huang变换（HHT）是一种强大的数据分析技术，尤其适用于处理那些在时间和频率上都具有变化特性的信号，即非线性、非平稳信号。这一方法的两个核心组成部分是经验模态分解（EMD）和希尔伯特谱分析。 1. 经验模态分解（EMD） EMD是一种数据驱动的信号分解方法，它将复杂信号分解为一系列内在模态函数（Intrinsic Mode Function, IMF）。IMF具有两个特征：局部特征时间和局部平均频率。EMD的过程包括迭代地找出信号的局部最大值和最小值，然后构建高斯样式的包络线，以此为基础提取IMF。这种方法能够适应信号的瞬时频率变化，使得每个IMF都对应着信号的一个特定成分或特征。 2. 希尔伯特谱分析 在EMD之后，希尔伯特谱分析被用来计算每个IMF的瞬时幅度和瞬时频率。通过构造希尔伯特变换（Hilbert Transform），可以为每个IMF得到对应的希尔伯特变换函数，从而得到信号的瞬时频谱。希尔伯特谱提供了信号随时间变化的幅度和频率信息，使得对非平稳信号的动态特性分析成为可能。 3. 应用领域 HHT在多个科学领域有广泛应用，包括但不限于： - 地球科学：如地震信号分析，气候变化研究； - 海洋学：海洋流速、海浪动力学分析； - 大气科学：气象预测，大气湍流研究； - 工程学：机械振动分析，电力系统稳定性研究； - 医学：生物信号处理，如心电信号、脑电图等。 4. 优势与挑战 HHT的主要优点在于其对非线性、非平稳信号的适应性和解析能力。然而，EMD过程可能存在一些问题，如模式混叠、过度分解或欠分解等，这需要在实际应用中进行细致的调整和验证。此外，HHT的计算量较大，对于大规模数据的处理可能效率较低。 Hilbert-Huang变换提供了一种有效的工具，用于理解和解析那些传统傅立叶分析方法难以处理的复杂信号。通过EMD和希尔伯特谱分析的结合，科学家和工程师能够深入洞察非线性、非平稳系统的动态行为。