EM算法入门:高斯混合模型详解与MATLAB实现
需积分: 9 179 浏览量
更新于2024-09-09
收藏 411KB PDF 举报
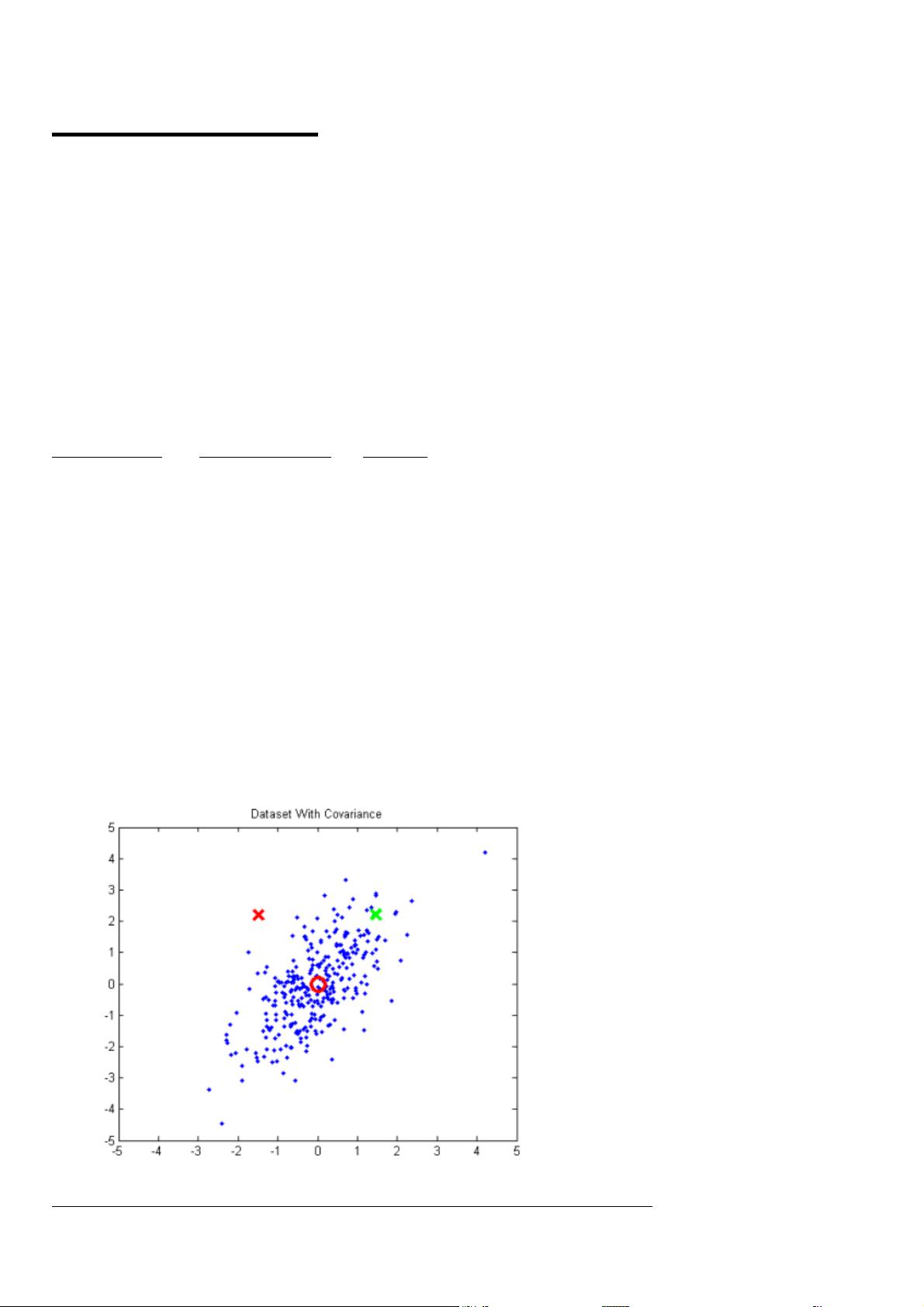
EM算法(Expectation-Maximization Algorithm)是一种在概率模型参数估计中广泛应用的迭代优化方法,尤其在机器学习领域,如高斯混合模型(Gaussian Mixture Models, GMMs)的训练中发挥着关键作用。GMM是一种统计建模工具,它假设数据点由多个互相独立的高斯分布(每个都有自己的均值和协方差矩阵)组成,而非像k-means那样所有数据点都集中在单个球形集中。
该文档提供了一个清晰易懂的GMM教程,并附有MATLAB代码,作者是Chris McCormick。在GMM中,"E-step"(期望步骤)和"M-step"(最大化步骤)构成了EM算法的核心循环。E-step计算每个数据点属于各个高斯成分的概率,而M-step则基于这些概率更新每个高斯分布的参数,如均值和协方差矩阵。这种迭代过程旨在最大化似然函数,即使数据的分布不是完全符合高斯假设时也能找到一个接近的最佳模型。
与k-means聚类相比,GMM的一个主要优势在于处理数据的复杂性。k-means依赖于欧几里得距离,对具有显著协方差的集群效果不佳,因为它假设数据点均匀分布在簇内。然而,GMM能更好地适应这样的数据特性,即使数据点在空间上可能不是严格的球形分布,通过多峰分布的组合,它仍然可以捕捉到数据的潜在结构。
在实际应用中,GMM广泛用于诸如密度估计、分类、图像分割、文本分析等领域。通过理解和实现EM算法,数据科学家可以构建更精确的模型,适应各种类型的非线性数据分布。同时,该文档提供的MATLAB代码对于初学者来说是一个宝贵的实践资源,可以直接应用于实际项目中,提升对GMM的理解和使用能力。
2021-05-26 上传
点击了解资源详情
2021-05-26 上传
2011-12-13 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
知行力
- 粉丝: 12
- 资源: 7
最新资源
- JavaScript实现的高效pomodoro时钟教程
- CMake 3.25.3版本发布:程序员必备构建工具
- 直流无刷电机控制技术项目源码集合
- Ak Kamal电子安全客户端加载器-CRX插件介绍
- 揭露流氓软件:月息背后的秘密
- 京东自动抢购茅台脚本指南:如何设置eid与fp参数
- 动态格式化Matlab轴刻度标签 - ticklabelformat实用教程
- DSTUHack2021后端接口与Go语言实现解析
- CMake 3.25.2版本Linux软件包发布
- Node.js网络数据抓取技术深入解析
- QRSorteios-crx扩展:优化税务文件扫描流程
- 掌握JavaScript中的算法技巧
- Rails+React打造MF员工租房解决方案
- Utsanjan:自学成才的UI/UX设计师与技术博客作者
- CMake 3.25.2版本发布,支持Windows x86_64架构
- AR_RENTAL平台:HTML技术在增强现实领域的应用