冈萨雷斯《数字图像处理》第4章:频率域图像增强
需积分: 9 28 浏览量
更新于2024-08-02
收藏 5.18MB PPT 举报
"冈萨雷斯《数字图象处理》第4章主要讲解了频率域中的图像增强技术,涉及傅里叶变换的基础知识及其在图像处理中的应用。"
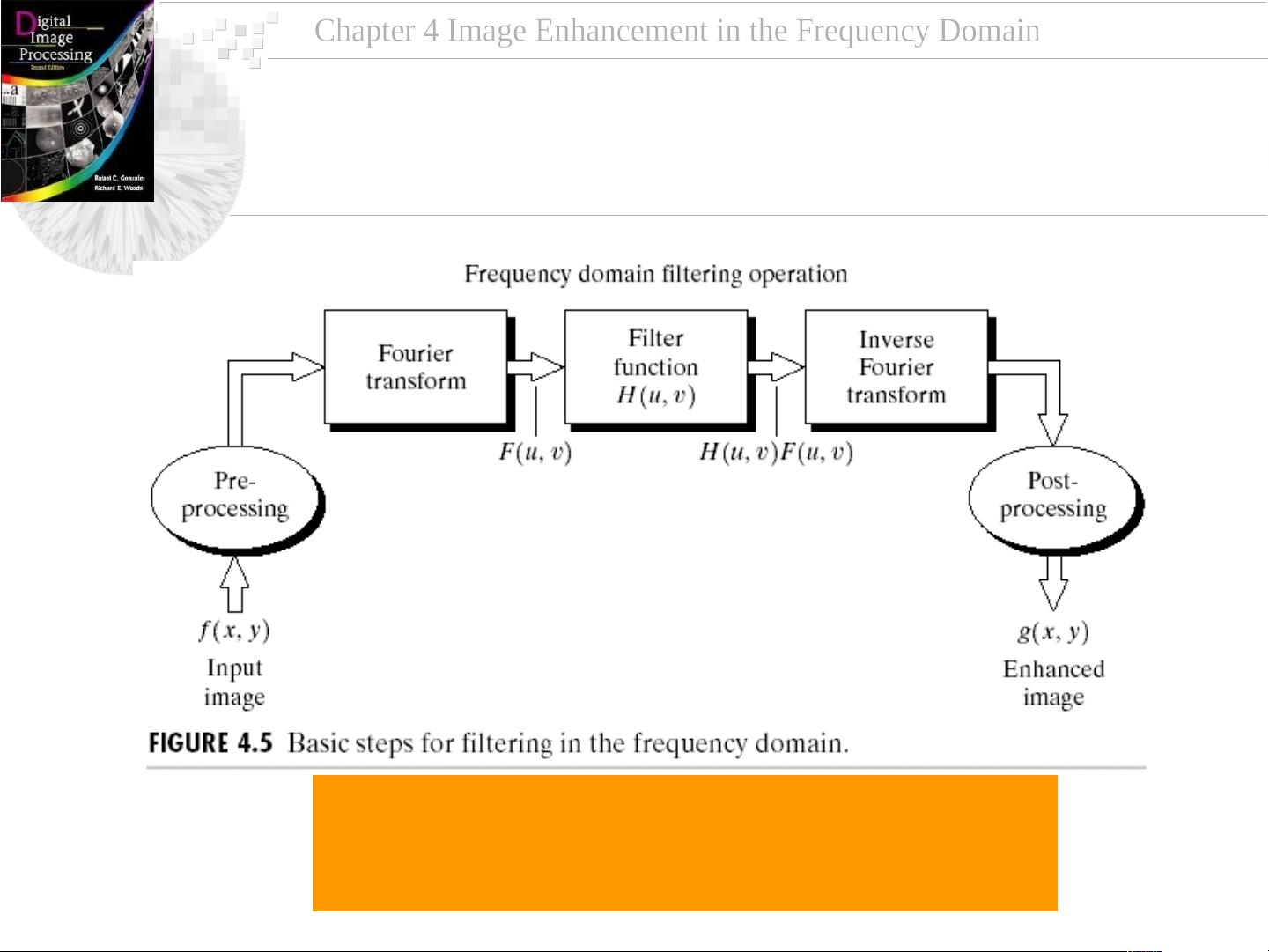
本章主要探讨了图像增强的一个重要领域——频率域中的图像处理。频率域的概念在数字图像处理中至关重要,因为它提供了一种分析图像特征的新视角。傅里叶变换是这个领域的一个核心工具,它允许我们将图像从空间域转换到频率域,以便更好地理解和操纵图像的频谱特性。
傅里叶变换是1807年由傅里叶提出的理论,他提出任何周期性函数都可以表示为正弦和余弦函数的加权和。这一理论在当时并未被广泛接受,但随着时间的发展,它已经成为数学和工程领域中的一个基础工具。
在图像处理中,傅里叶变换用于将图像的像素值分布(空间域)转化为频率成分(频率域)。2D离散傅里叶变换(2D DFT)是实现这一转换的常见方法,其公式如下所示:
\[ F(u, v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j2\pi(\frac{ux}{M} + \frac{vy}{N})} \]
这里,\( F(u, v) \) 是图像 \( f(x, y) \) 的傅里叶变换,\( M \) 和 \( N \) 分别为图像的宽度和高度,\( u \) 和 \( v \) 是频率坐标。
傅里叶变换的结果,即傅里叶谱,包含了图像的所有频率信息。高频率对应于图像的细节和边缘,而低频率则代表图像的整体亮度和颜色变化。通过操作傅里叶谱,可以对图像进行增强或滤波,例如通过增加或减少某些频率成分来突出或抑制特定图像特征。
傅里叶变换的逆变换则将频率域的图像变换回空间域,这样经过处理后的频率信息就能以图像的形式重新展现出来。2D离散傅里叶逆变换(2D IDFT)公式如下:
\[ f(x, y) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) e^{j2\pi(\frac{ux}{M} + \frac{vy}{N})} \]
通过这个过程,我们可以实现对图像的频率域增强,比如平滑噪声、锐化图像或增强特定频率的细节,进而改善图像的整体视觉效果。
冈萨雷斯《数字图象处理》第4章深入介绍了频率域中的图像增强技术,包括傅里叶变换的基本概念、2D DFT和2D IDFT的计算,以及如何利用这些工具来优化和解析图像的频率特性。这些知识对于研究生级别的数字图像处理研究和实践至关重要。
2009-12-11 上传
2011-12-20 上传
117 浏览量
2009-12-11 上传
2009-09-06 上传
2009-12-11 上传
109 浏览量
2011-11-22 上传
xiaowenleo
- 粉丝: 1
- 资源: 13