特征值与奇异值分解：矩阵分析在机器学习中的应用

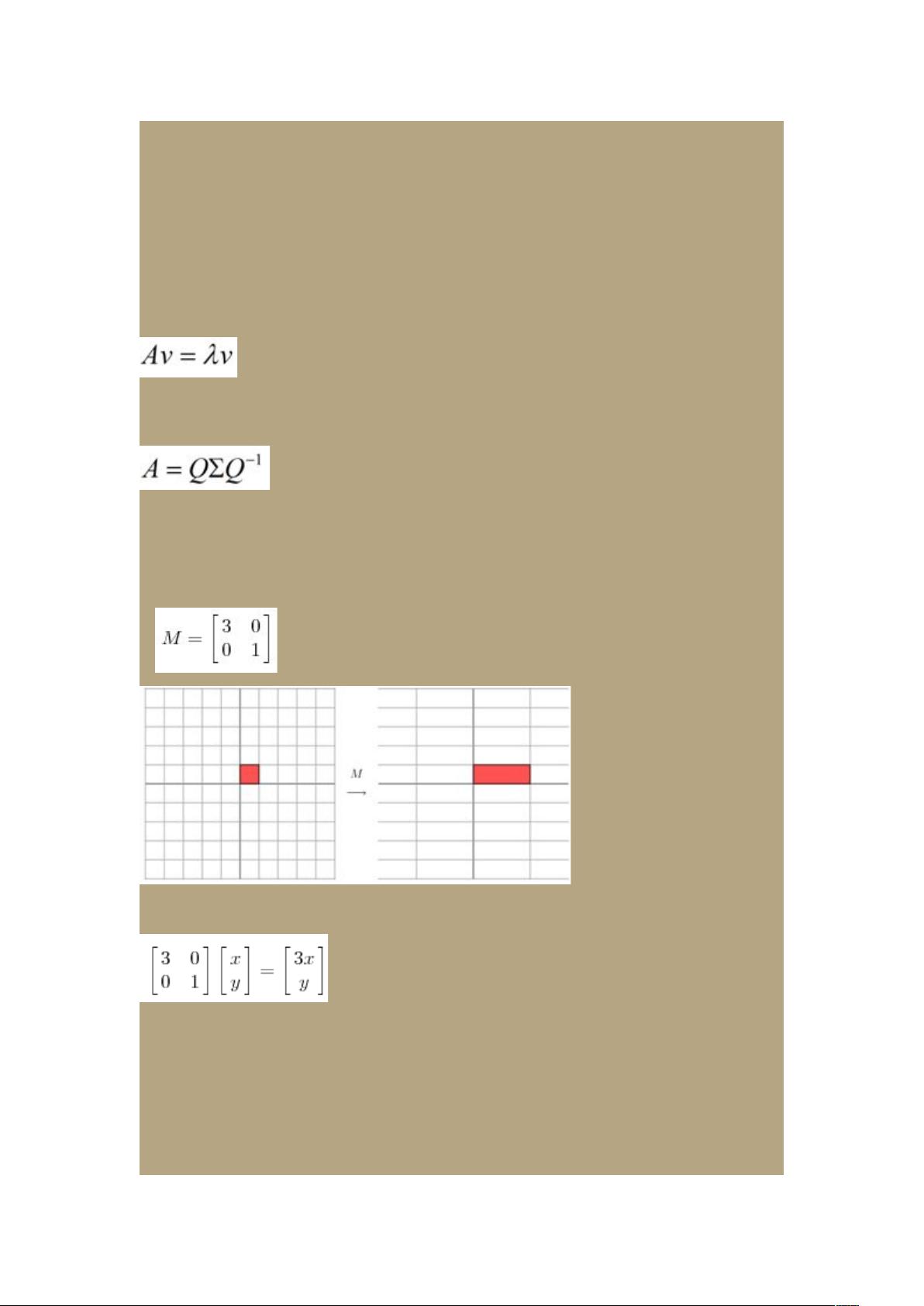
解： 奇异值分解（Singular Value Decomposition，简称SVD）是线性代数中的另一个重要概念，它与特征值分解密切相关，但适用范围更广。特征值分解主要针对方阵，而奇异值分解可以应用于任意大小的矩陣。 1）奇异值： 奇异值分解将一个矩阵A（不一定是方阵）分解为三个矩阵的乘积： 其中U是A左奇异向量组成的列矩阵，Σ是一个对角矩阵，其对角线上的元素称为奇异值，V是A右奇异向量组成的列矩阵，且U和V的列向量均为单位正交向量。与特征值分解类似，奇异值也体现了矩阵变换的主要特征，但它们的含义有所不同。奇异值σ_i反映了矩阵A在不同方向上压缩或膨胀的程度，从大到小排序，最大的奇异值σ_1对应于矩阵A最强的伸缩方向。 2）奇异值与特征值的关系： 对于实对称矩阵，它的特征值分解和奇异值分解有直接联系。实对称矩阵的特征值是其奇异值的平方，即如果λ是特征值，则相应的奇异值σ=√λ。此外，特征向量和奇异向量之间也有特定关系。在实对称矩阵的情况下，特征向量与奇异向量是正交的，并且可以选取为标准正交基。 3）应用： 特征值分解和奇异值分解在许多领域都有广泛的应用，尤其是在机器学习和数据挖掘中。例如： - 数据降维：通过保留最大的几个特征值或奇异值，可以近似原矩阵，从而降低数据的维度，例如主成分分析（PCA）。 - 矩阵恢复：在稀疏数据或缺失数据的情况下，可以通过特征值或奇异值进行插值，恢复矩阵。 - 图像处理：在图像压缩中，奇异值分解可以有效地去除图像噪声，只保留重要的信息。 - 因子分析：在统计学中，特征值分解常用于因子分析，找出隐藏的变量结构。 - 机器学习模型的正则化：在训练模型时，如逻辑回归或支持向量机，通过对权重矩阵进行奇异值分解，可以进行L1或L2正则化，防止过拟合。 4）局限性： 尽管奇异值分解非常强大，但也存在一些限制。计算奇异值分解可能需要较高的计算成本，特别是对于大规模矩阵。此外，奇异值分解对噪声敏感，当数据中存在噪声时，可能会导致不准确的结果。 特征值分解和奇异值分解是线性代数中强大的工具，它们帮助我们理解和简化复杂的矩阵操作，特别是在处理高维数据时。通过提取矩阵的主要特征，我们可以更好地理解和建模数据，从而在各种实际问题中找到解决方案。