Oj
hput Layer HidnLyer Output Luyer
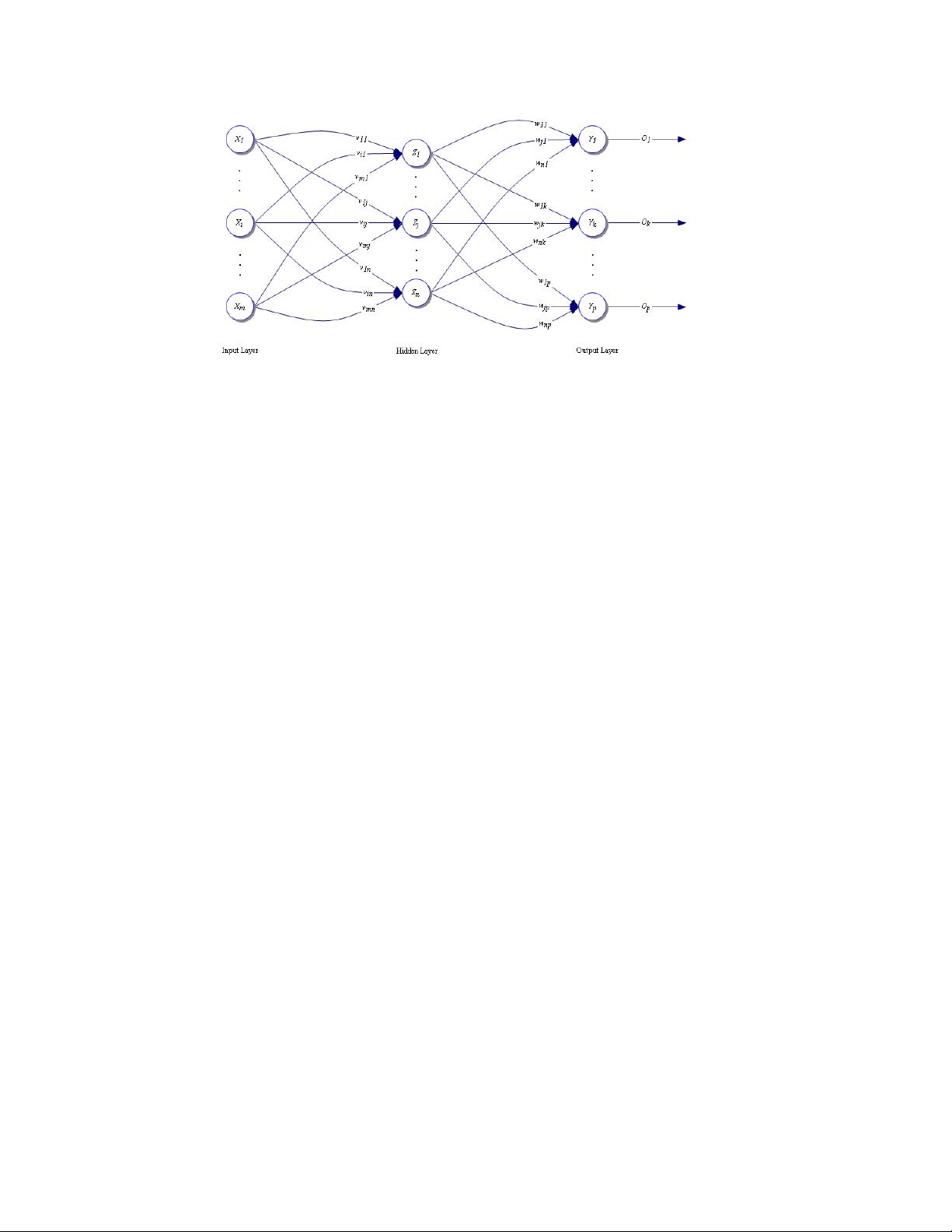
Fig. 1.1: Feed-forward artificial neural network Adapted from [5]
A neural network operates similar to the nervous system of animals in that it is a system of connected nodes,
activated when sufficient incoming signals are received. Each node has a binary activation of active or not, or 1 or 0
respectively, along with partial activations, between 0 and 1 to account for approximations, or “fuzzy logic.” If a
node is activated, it sends a signal out to the next set of nodes. Each connection between a node and the next layer of
nodes has a weighted value as well, affecting how the outputs of each node affect the next receiving node. The
system then “learns” from training examples by optimizing these inter-nodal weights to obtain an ideal input to
output operation. The architecture of the networks used in part of this investigation was a simple one-way network,
consisting of layers of nodes, which affect the next layer. No connections go backward through the network, so that
the process is not time dependant, and thus most suitable for this problem. The input variables form their own, first
set or layer of nodes in the network, then several sets of nodes, called hidden layers, follow. Fig. 1.1 illustrates a
feed-forward network with only one hidden layer; however, multiple hidden layers may be added as well. The final
layer of nodes is the output set, representing the output of the entire network.
Artificial neural networks optimize these inter-nodal weights by "learning" a data set of inputs to outputs, using a
training data set. This is usually a general sweep of combinations of inputs to outputs, which the network would
encounter in operation. The neural network, once taught a set of inputs to outputs, is then used with data sets, which
fall within the range of the learning data set. The advantage of the neural network lies in its ability to use this
learning procedure to approximate outputs associated with approximate inputs, which would otherwise require a
strenuous, time-consuming method to determine the appropriate input/output relationship. Crack detection in an
aircraft SHM system requires fast, accurate detection and analysis of the condition of structural components in flight
to assure that damage is recognized before structural failure.
Each node of the network follows a mathematical model represented by Eq. (1.1) below, where function, f, is a
sigmoid function and notation is derived from Fig. 1.1.
Here, the sum of the weighted outputs of the hidden layer, Z
j
, which are connected to node k in the output layer, go
into an activation function, which then becomes the output for node k in the output layer, O
k
. This equation shows
the model for a node in the output layer, but it also applies to all other nodes in other layers as well. Unlike serial or
digital computers, where the activation function is limited to a hard threshold of on or off (1 or 0 respectively),
neural networks allow for smooth transitions, resulting in better approximations of similar functions.
Adjustment of the weights between the nodes comes about through a method discovered by Rumelhart, Hinton and
Williams
5
, which involves taking the error between the desired outputs, t
k
, and the output obtained by the network,
O
k
, and adjusting the weights, which in Fig. 1.1 and Eq. (1.1) is weights w
jk
, using the following equation.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
∑
=
n
j
jjkk
ZwfO
1
(1.1)
Proc. of SPIE Vol. 7295 729507-3
Downloaded from SPIE Digital Library on 01 Feb 2010 to 59.66.44.2. Terms of Use: http://spiedl.org/terms









