Java实现堆排序算法详解

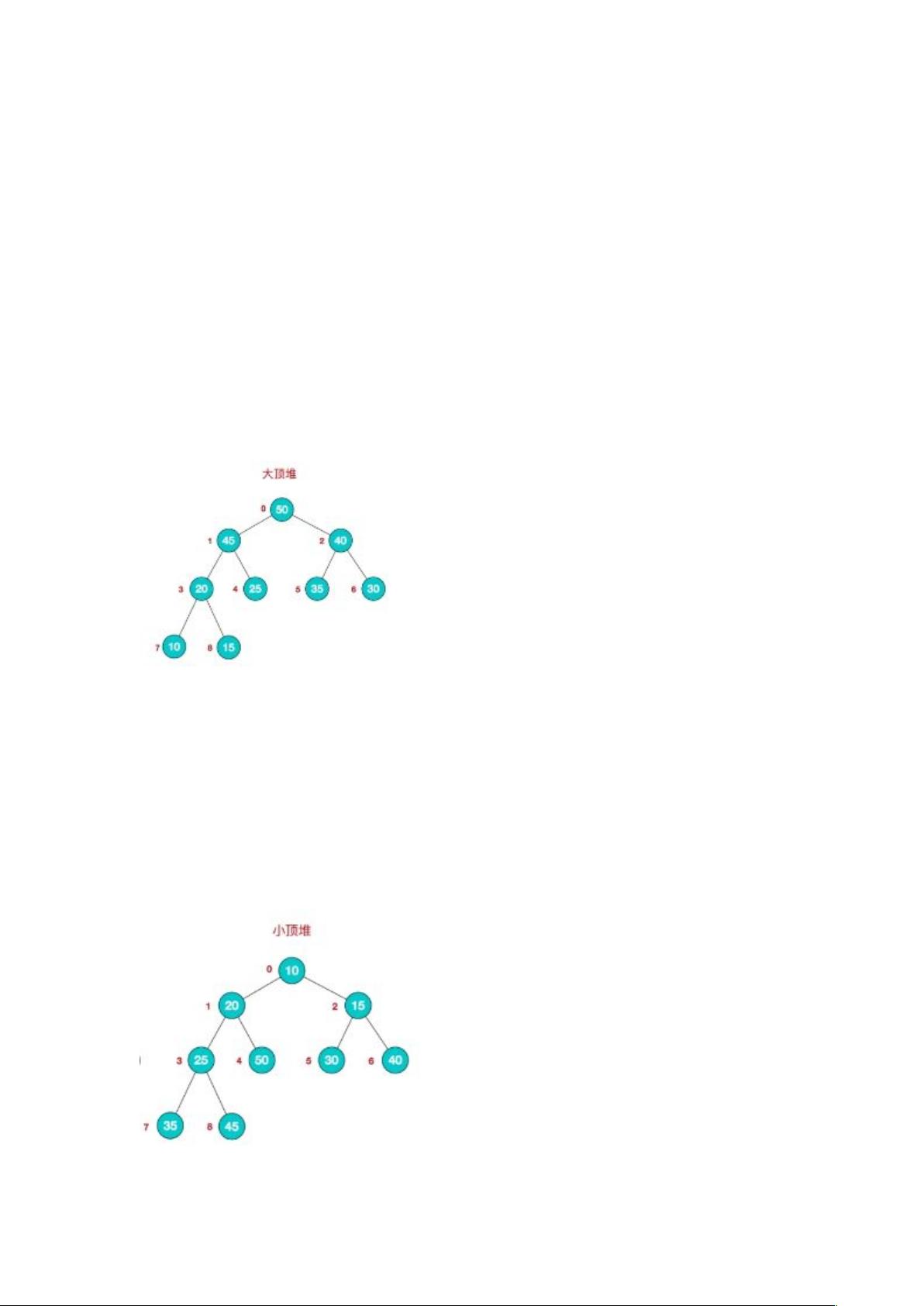
"java的选择排序之堆排序" 堆排序是一种高效的排序算法，它的基本思想是将待排序的序列构建成一个大顶堆（或小顶堆），使得堆顶元素（最大值或最小值）总是位于序列的起始位置。然后通过交换堆顶元素与末尾元素并重新调整堆的过程，逐步将无序序列转换为有序序列。 在堆排序的过程中，大顶堆的特点是每个父节点的值都大于或等于其子节点的值。用数组表示时，如果i是父节点的位置，则其左子节点为2i+1，右子节点为2i+2，且满足条件arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]。相反，小顶堆则是每个父节点的值小于或等于其子节点的值，满足arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]。 堆排序的基本步骤如下： 1. 构建初始堆：从最后一个非叶子节点（即数组长度除以2减1的下标处）开始，自底向上调整每个节点，确保其满足大顶堆或小顶堆的性质。这个过程通常被称为heapify或调整堆。 2. 交换堆顶元素与末尾元素：将最大值（大顶堆）或最小值（小顶堆）与末尾元素交换，然后将末尾元素剔除，此时末尾元素即为排序后的最大值或最小值。 3. 重新调整堆：对剩余的n-1个元素再次进行堆化操作。 4. 重复步骤2和3，直到堆的大小为1，此时整个序列已经按照升序或降序排列完成。 在给出的代码示例中，`HeapSort`类包含了一个`heapSort`方法，该方法实现了堆排序的逻辑。首先，通过一个循环生成一个包含8000000个随机整数的数组，然后调用`heapSort`方法对数组进行排序。在排序过程中，`adjustHeap`方法用于调整堆，确保堆的性质。在排序完成后，计算并输出排序所需的时间，从而评估算法的效率。 堆排序的时间复杂度在最坏、最好和平均情况下都是O(nlogn)，这使得它在处理大数据量时具有较好的性能。然而，由于堆排序不是稳定的排序算法，相同元素的相对顺序可能会在排序后改变。此外，堆排序在原地排序，不需要额外的存储空间，这是它的一个优点。 总结来说，堆排序是一种基于堆数据结构的排序算法，通过构建和调整堆来达到排序的目的，其时间复杂度为O(nlogn)，适用于大规模数据的排序，但不保证稳定性。