信息论与编码：马尔可夫信源与骰子投掷的熵分析

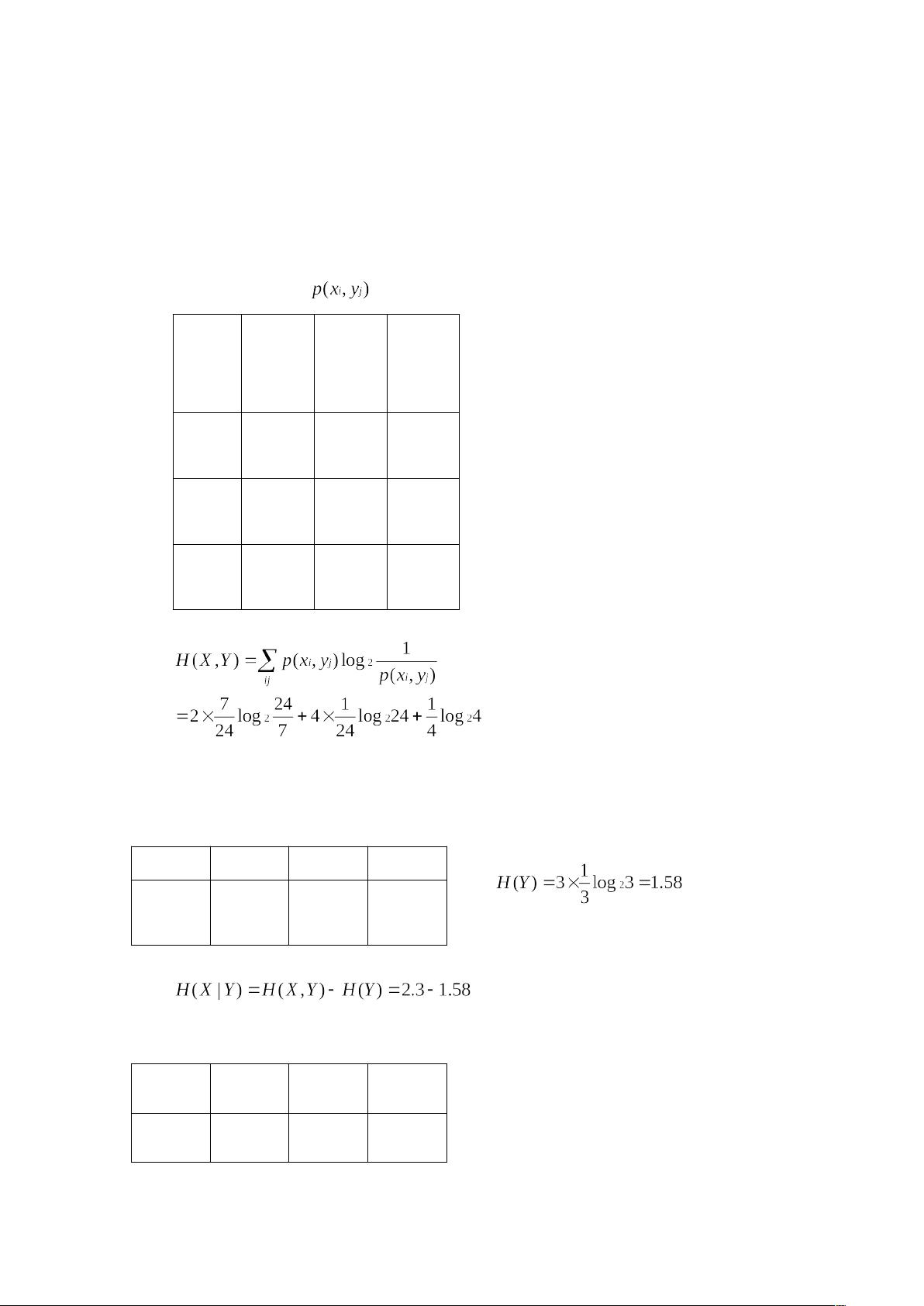
《信息论与编码》是一本关于信息理论和编码技术的经典教材，由作者曹雪虹编写，旨在帮助读者理解和应用信息论的基本原理。课后习题涵盖了一系列关键概念和实践问题，包括马尔可夫信源的分析、状态概率计算以及信息熵的测量。 在第二章中，首先探讨的是马尔可夫信源的问题。信源有三个符号，转移概率通过给出的具体数值构成状态转移矩阵。要求学生绘制状态图并求出每个符号在稳定状态下的概率。通过计算，学生需要找到每个状态的稳态概率，这是理解信源平稳性的基础。 接着，讨论了二阶马尔可夫链，这是一种序列模型，其转移概率特定于前两个符号的状态。学生需要根据给定的概率值构建状态图，同样求解稳态概率分布。 接下来的题目涉及到掷骰子的实验，涉及的信息论概念包括自信息、熵和平均信息量。例如，计算特定事件如“3和5同时出现”或“两个1同时出现”的自信息量，反映了这些事件发生的不确定性。对于所有可能的点数组合的熵和平均信息量的计算，有助于了解随机过程的信息内容总体水平。 针对两个骰子的总和，问题要求计算其熵，即各种可能结果的不确定性。最后，通过生活中的实例，询问“身高160厘米以上的女孩是大学生”这一信息带来的信息量，体现了信息论在实际决策中的应用，即通过条件概率计算信息增益。 这些习题旨在让学生运用信息熵、马尔可夫链等理论工具，分析和解决实际问题，提升他们对信息传输和处理的理解能力。通过解答这些问题，学生将加深对信息论基本概念的理解，如概率、依赖性和随机过程，这对于通信工程、数据压缩、信号处理等领域具有重要意义。