COL 9(12), 120006(2011) CHINESE OPTICS LETTERS December 10, 2011
Computer-generated image hologram
Takeshi Yamaguchi
∗
and Hiroshi Yoshikawa
Department of Electronics and Computer Science, College of Science and Technology,
Nihon University 7-24-1 Narashinodai, Funabashi-shi, Chiba 274-8501, Japan
∗
Corresp onding author: yamaguchi@ecs.cst.nihon-u.ac.jp
Received July 26, 2011; accepted September 15, 2011; posted online November 25, 2011
We investigate the computer-generated hologram with full parallax and which can be reconstructed with
white light. The object of the hologram is processed from three-dimensional computer graphics polygon
data and has shaded surface for hidden surface removal. The optically reconstructed image from the
printed hologram is evaluated.
OCIS codes: 090.0090, 090.1760.
doi: 10.3788/COL201109.120006.
The hologram has three-dimensional (3D) information
such as the binocular parallax, the convergence, and ac-
commodation. Therefore, the reconstructed image of the
hologram provides natural spatial effect. In particular,
the viewer gets strong dimensional impression when the
image is popping up from the hologram plane.
We have been studying computer-generated hologram
(CGH), whose interference fringes are calculated on the
computer. We have also developed the output device
of the CGH, which is called fringe printer. The im-
proved fringe printer
[1]
is able to provide the 0.44 µm
pitch and over 100 Gpixels hologram. Using this fringe
printer, we have printed the computer-generated Fres-
nel hologram
[1]
(CGFH), the computer-generated rain-
bow hologram
[2]
(CGRH), the computer-generated cylin-
drical hologram
[3]
(CGCH), the computer-generated disk
hologram
[4]
(CGDH), and the computer-generated alcove
hologram
[5]
(CGAH). There are also some published pa-
pers about printed CGH
[6−9]
. However, most CGHs are
of Fresnel type
[7−9]
. Therefore, CGHs require the laser
or the single color LED for the illumination. Reference
[6] can be reconstructed by white light. However, this
CGH only has the horizontal parallax. Since the pixel
pitch of the CD-R is not enough for the 3D CGH, the
viewing angle is not enough. In addition, proper hidden
surface removal is necessary when the pixel pitch of the
output device becomes fine.
In this letter, we investigate the image type CGH,
which is the output of the fringe printer. We propose
the modified hidden surface removal method for the im-
age type CGH. We calculate and output the CGH of
the shaded object processed from the computer graph-
ics polygon data. The reconstructed images show proper
hidden surface removal and full parallax.
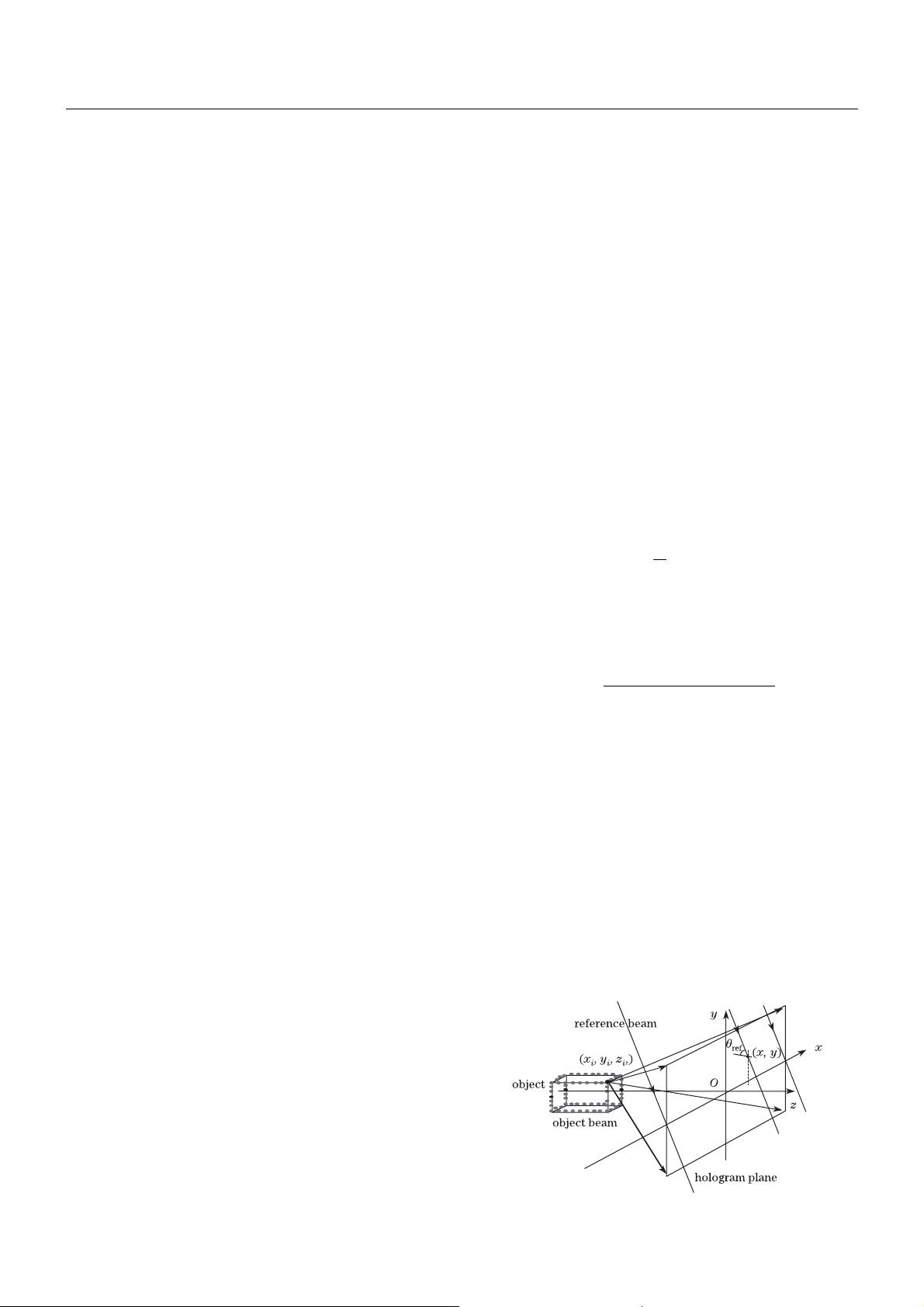
The rigorous calculation method described in this sec-
tion is based on an exact optical model. The object
to be recorded is approximated as a collection of self-
illuminated points
[10]
, and located at a certain point in a
system of Cartesian coordinates. The calculation geom-
etry of the hologram is shown in Fig. 1.
The hologram is located on the xy-plane, and the ob-
server’s side takes positive value of the z-axis. The lo-
cation of the ith object point is specified as (x
i
, y
i
,
z
i
). Each point has real-valued amplitude a
i
and relative
phase φ
i
. The complex amplitude O(x, y) on the holo-
gram is determined from the superposition of the object
wavefronts by
O(x, y) =
N
X
i=1
a
i
r
i
exp[j(kr
i
+ φ
i
)], (1)
where N is the number of object points. The wave num-
ber k is defined as k = 2π/λ, where λ is the free-space
wavelength of the light. The oblique distance r
i
between
the ith object point and the point (x, y) on the hologram
is defined as
r
i
=
q
(x − x
i
)
2
+ (y − y
i
)
2
+ z
2
i
. (2)
If the reference beam is collimated, the complex ampli-
tude of the reference beam R(x, y) is represented as
R(x, y) = a
R
exp(jky sin θ
ref
), (3)
where a
R
is the real-valued amplitude and θ
ref
is the in-
cident angle of the reference beam. The total complex
amplitude on the hologram plane is the interference of
the object beam and the reference b eam represented as
O(x, y)+R(x, y). The total intensity pattern,
I(x, y) = |O + R|
2
= |O|
2
+ |R|
2
+ 2Re{OR
∗
}, (4)
is a real physical light distribution on the hologram,
where Re{C} takes the real part of the complex number
C, and R* means the conjugate of R. The first term rep-
resents the object self-interference and the second term
Fig. 1. Model to calculate the Fresnel hologram.
1671-7694/2011/120006(4) 120006-1
c
° 2011 Chinese Optics Letters









