拉普拉斯变换与系统稳定性分析

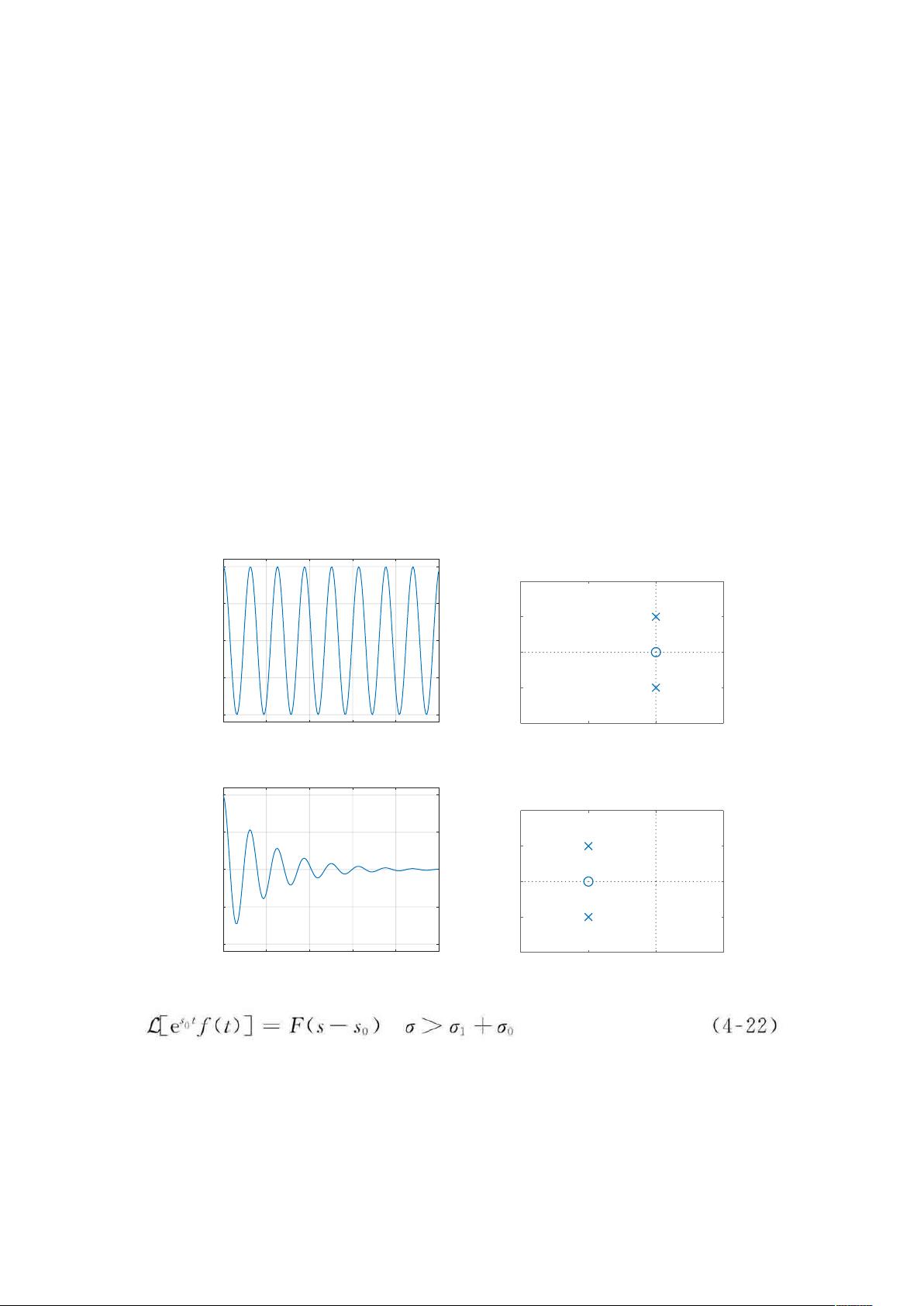
"本文档主要介绍了拉普拉斯变换和拉普拉斯分析在信号与系统中的应用，涉及MATLAB的计算方法。内容包括从傅里叶变换到拉普拉斯变换的转换，双边拉普拉斯变换的收敛域特性，单边拉普拉斯变换的定义以及MATLAB中的实现，以及单边拉普拉斯变换的性质。" 拉普拉斯变换是一种在信号处理和控制系统理论中广泛使用的数学工具，它可以将时域中的信号转换到复频域，以便于分析和设计系统。当傅里叶变换不适用于非绝对可积的信号时，拉普拉斯变换提供了一个扩展的框架。通过在信号f(t)前乘以衰减因子e^(-σt)，并令s=σ+jω，可以得到双边拉普拉斯变换，即F(s)=∫_{-\infty}^{+\infty} f(t)e^{-st}dt。 双边拉普拉斯变换的收敛域至关重要，它是信号f(t)e^(-σt)绝对可积的σ值集合。这个区域必须不包含任何极点，且其边界是平行于jω轴的直线。对于因果信号，其双边拉普拉斯变换的收敛域位于所有极点的右半平面；对于反因果信号，它位于所有极点的左半平面；非因果信号的收敛域是因果部分和反因果部分收敛域的交集。 单边拉普拉斯变换主要应用于实际的因果信号，即t<0时f(t)=0的信号。单边变换的定义消除了负无穷的时间积分，从而简化了收敛条件。在MATLAB中，可以使用`laplace`函数求解单边拉普拉斯变换，如示例所示，计算了单位冲激函数、单位阶跃函数、阶跃函数的差分以及指数函数的单边拉普拉斯变换。 此外，单边拉普拉斯变换还具有线性和时移等基本性质，这对于理解和应用变换极其重要。线性性质表明，如果f(t)和g(t)的单边拉普拉斯变换分别是F(s)和G(s)，那么af(t)+bg(t)的单边拉普拉斯变换为aF(s)+bG(s)。时移性质则说明，信号f(t-a)的拉普拉斯变换为e^{-as}F(s)，其中F(s)是f(t)的拉普拉斯变换。 周期信号的拉普拉斯变换也遵循特定规则，通常需要用到傅里叶级数来展开周期信号，然后对每个傅里叶系数进行拉普拉斯变换。 总结来说，拉普拉斯变换在信号与系统的分析中起到了桥梁的作用，它连接了时域和复频域，使得我们能够更深入地理解信号的行为和系统响应，特别是在系统稳定性、控制理论和滤波器设计等领域。MATLAB提供的工具使得这些计算变得直观且易于执行，进一步推动了理论研究和工程实践的结合。