深度优先遍历在图数据结构中的应用与解析

"漫话数据结构-深度优先遍历.pptx" 在计算机科学中，数据结构是组织、存储和处理数据的一种方式，它能够高效地实现特定算法。本资源聚焦于数据结构中的一个重要概念——遍历，特别是深度优先遍历（DFS, Depth-First Search）。遍历对于理解和操作数据结构至关重要，因为许多算法的核心都涉及到遍历数据结构的所有元素。 遍历是指按照一定的顺序访问数据结构中的每个元素。在图和树这两种数据结构中，遍历的方法有所不同。对于二叉树，遍历通常分为三种类型：前序遍历（Preorder）、中序遍历（Inorder）和后序遍历（Postorder）。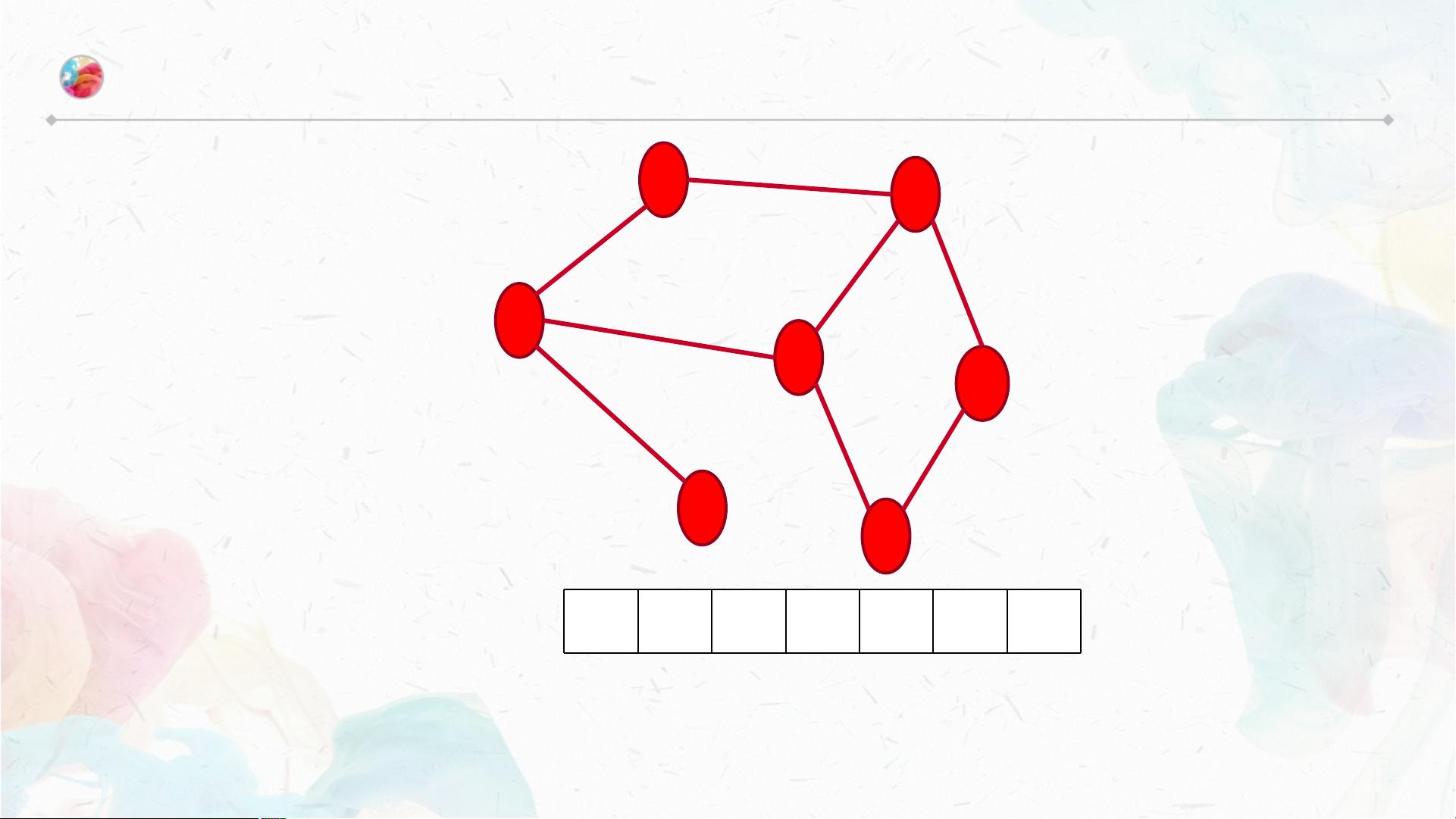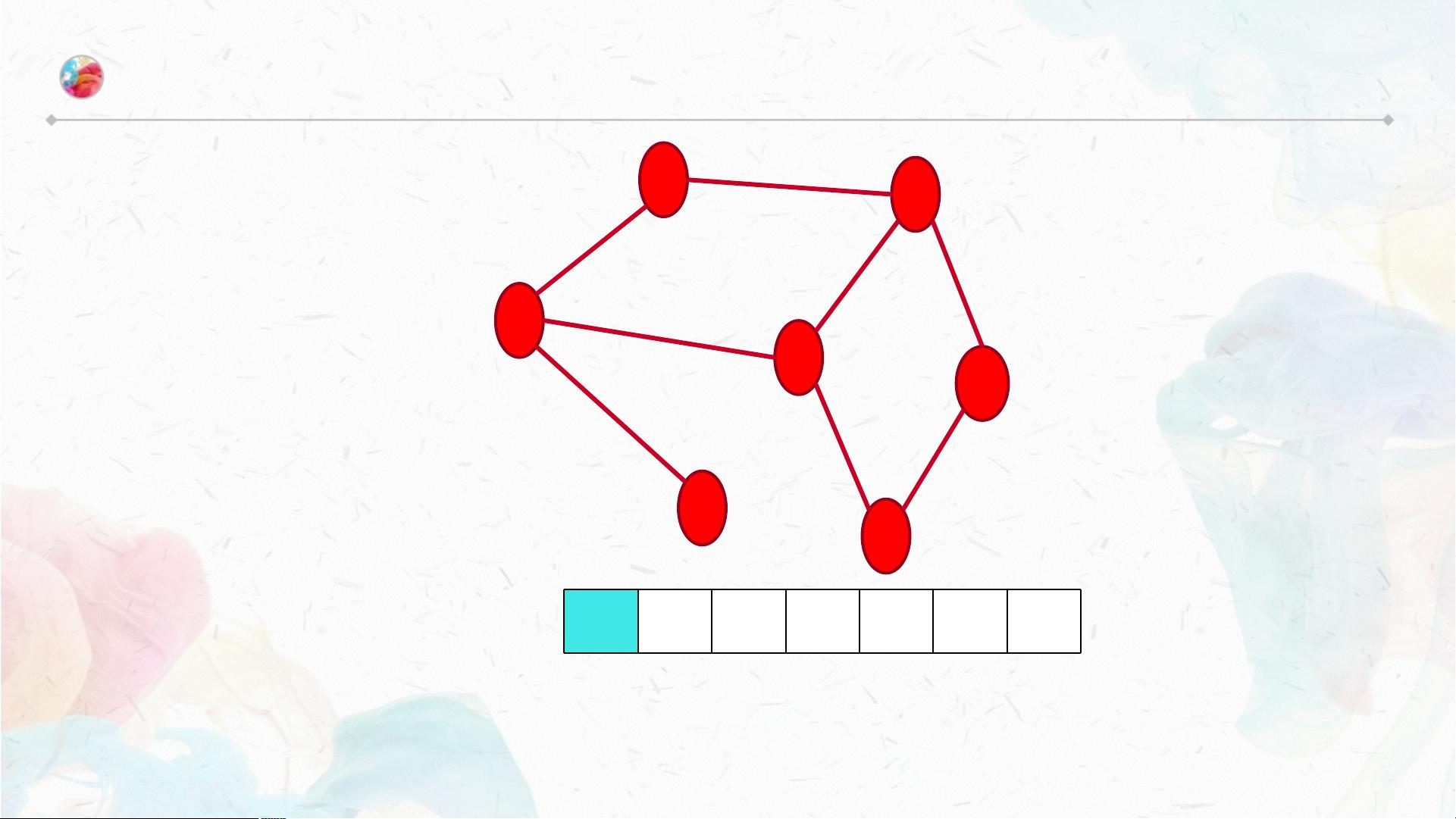例如，前序遍历的顺序是根节点→左子树→右子树，如代码所示： ```java preorder(root); preorder(TreeNodenode){ if(node!=null){ list.add(node.val); preorder(node.left); preorder(node.right); } } ``` 在图的遍历中，由于可能存在环，所以需要跟踪已访问过的节点，以避免无限循环。深度优先遍历是通过递归的方式进行的，从一个节点开始，沿着边尽可能深地搜索图的分支，直到达到叶子节点，然后回溯。在Java代码中，DFS的实现可能如下： ```java visited[0…V-1]=false; dfs(0); dfs(int v){ visited[v]=true; list.add(v); for(int w: adj(v)){ if(!visited(w)) dfs(w); } } ``` 深度优先遍历适用于解决多种问题，尤其是在面试中，对于图相关的问题，大约80%可以通过DFS来解决。例如，判断图中是否存在环、寻找最短路径等。在给定的示例中，展示了如何对图进行DFS，并给出了不同的遍历顺序，例如：0→1→2、1→0→3→4、2→0→3→6等。 在DFS过程中，函数的递归调用也是关键。例如，`funcA()` 可能会调用 `funcB()`，`funcB()` 又会调用 `funcC()`，这就类似于图中的边，形成一个调用链。同时，存在多个互相独立的调用路径，例如 `funcA()` 可能直接或间接地调用自身，这在图的表示中就会形成多条从一个节点到另一个节点的路径。 深度优先遍历是理解和解决问题的重要工具，尤其在处理图和树这样的数据结构时。掌握好DFS的概念和实现方法，将有助于解决实际的编程问题和算法挑战。