深度学习：Xavier初始化在深度前馈网络中的应用解析

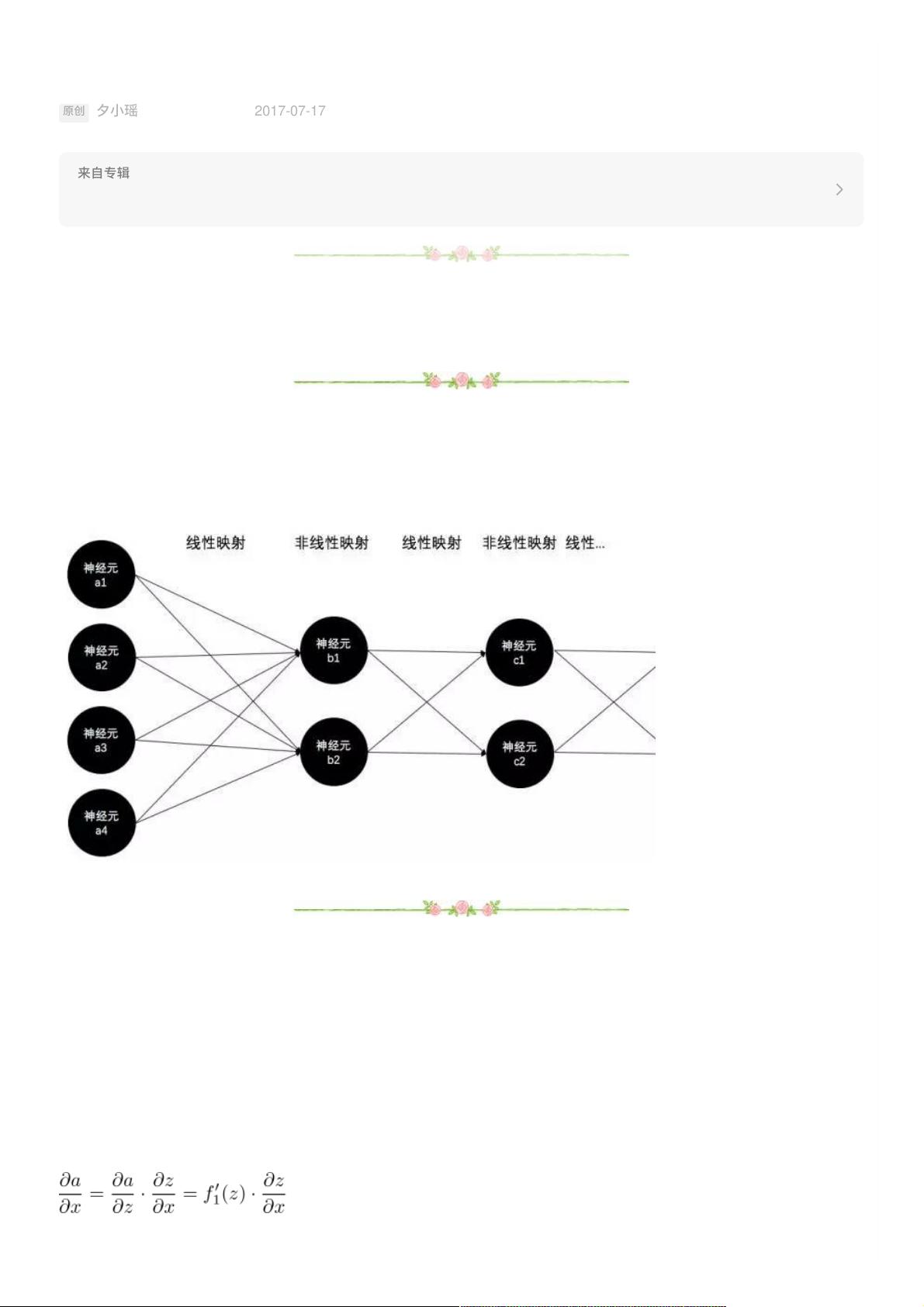
"本文深入探讨了深度前馈网络的反向传播过程和Xavier初始化原理，适合对机器学习和AI有深入了解的读者。" 深度前馈网络（Deep Feedforward Network）是一种基本的神经网络架构，其中数据沿单向传递，从输入层通过隐藏层直至输出层。这种网络的核心组成部分是线性映射和非线性激活函数，这两者共同构建了网络的复杂性。 线性映射是每一层与下一层之间的连接，由权重矩阵表示。每个神经元的输出是输入与权重的乘积之和，即线性组合。非线性激活函数如Sigmoid、ReLU或Tanh则引入非线性，使网络能够学习更复杂的模式。 在反向传播过程中，误差从输出层向输入层反向传播，用于更新权重。这一过程基于链式法则和梯度下降，使得网络能根据预测错误调整权重。对于某层神经元，假设其输入为z，经过激活函数f1得到输出a。如果z是另一层的输出（通常由线性映射函数f2产生，即z=f2(x)），则在求梯度时，只需乘以f1的导数，即可忽略激活函数之后的影响，仅关注当前层及之前的变量。 对于线性层，其函数形式为f2(x)=w\cdot x，当误差反向传播至此，只需乘以权重w来继续传播。这个过程在深度网络中不断重复，通过乘以激活函数的导数和权重，逐步计算各层的梯度。 Xavier初始化，由Glorot和Bengio在2010年提出，是为了解决深度网络中梯度消失或爆炸的问题。该方法建议权重初始化的均值接近于0，方差根据输入和输出神经元的数量进行调整。具体来说，权重w的初始化应遵循以下公式： \[ Var(w) = \frac{2}{n_{in} + n_{out}} \] 其中，\(n_{in}\)是输入节点数，\(n_{out}\)是输出节点数。这样，初始化的权重既不会导致前几层的输出过于压缩（导致梯度消失），也不会过于放大（导致梯度爆炸），从而有利于训练过程的稳定进行。 除了Xavier初始化，还有其他初始化策略，如He初始化，特别适用于ReLU激活函数，它考虑了ReLU的非零导数期望，进一步优化了权重初始化。这些初始化技巧对于深度学习模型的训练至关重要，它们可以帮助网络更快地收敛，提高学习效果。 深度前馈网络的反向传播和Xavier初始化是理解神经网络优化和训练的关键概念。掌握这些原理有助于构建和训练更高效、更稳定的深度学习模型。在实际应用中，结合其他工程技巧，如正则化、优化算法和批量归一化，可以进一步提升模型的性能。